

L'étude de notre projet se porte sur une chaîne de pendules reliés entre eux par des ressorts et rebondissant sur un trampoline. Le but de la recherche est de prévoir le comportement d'un tel système en fonction de ses paramètres (constante de raideur et longueur avide des ressorts, constante de raideur du trampoline, masse), et plus précisemment s'il correspond à un système stable ou instable après perturbation.

Le système est composé de N masses identiques et reliées une à une par des ressorts de constantede raideur k. Les masses sont soumises à la force de gravitaion etrebondissent sur un trampoline assimilable à un ressort de constante de raideur C. On se place tout d'abord dans la situation d'équilibre la plus intuitive où toutes les masses sont alignées horizontalement et lachées sans vitesse initiale d'une certaine hauteur. Elles rebondissent alors toutes en même temps sur le trampoline de manière périodique.
Cette configuration de base va nous permettre de mesurer numériquement le seuil de stabilité, c'est-à-dire les valeurs des paramètres critiques à partir desquelles le système devient instable.Avant de se lancer dans cette étude, on réduit le nombre de paramètres en adimensionnant le problème: on obtient alors deux paramètres significatifs:
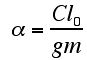
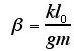
Pour étudier la stabilitéon va utiliser l'analyse de Floquet, c'est-à-dire qu'à partir de notre situation d'équilibre, on observe comment évolue le système si on lui soumet une perturbation même très petite. Pour certains paramètres le système revient à son état d'origine, pour d'autres il évolue de manière imprévisible à long terme. On a donc créé une simulation numérique qui permet à la fois la résolution du problème et la visualisation de notre chaîne de pendules, tout en faisant varier les paramètres à souhait.
Une fois les valeurs de paramètres entrées, le programme établit le mouvement après perturbation et lecompare au mouvement de la chaîne sans perturbation. On obtient alorsla matrice de monodromie du système. Si une de ses valeurs propresest de norme supérieure à 1 alors on peut prévoir quele système est instable, sinon il est stable. En répétant la simulation pour différents alpha on établit la loide stabilité.
Numériquement, on remarque donc que le système devient instable lorsque alpha est supérieur à 1,4 ( beta=0,1 ). Une autre sériede simulations a été effectué pour beta=1, on trouvealors le seuil de stabilité pour alpha= 18; alpha et beta sont doncbien les deux paramètres de contrôle.