III - Théorie de la diffraction

La microscopie électronique en transmission repose sur la diffraction d´un faisceau d´électron par un cristal. Nous allons donc faire une petite présentation des cristaux et nous intéresser aux conditions de diffraction. Il est à noter que l´on considère que le faisceau d´électrons se comporte comme une onde et que l'on peut donc observer des phénomènes de diffraction et d´interférences.

1 - Cristaux

Un cristal est un solide constitués d'atomes ordonnés les uns par rapport aux autres. Un cristal est caractérisé par un motif et une période spatiale (a, appelé également le paramètre de maille). Le motif est répété selon un réseau. La plus petite partie du réseau permettant de recomposer le cristal entièrement est appelée une maille.

Exemples de mailles de cristaux

On peut définir à partir de ces mailles des plans cristallins.

Exemples de plans cristallins

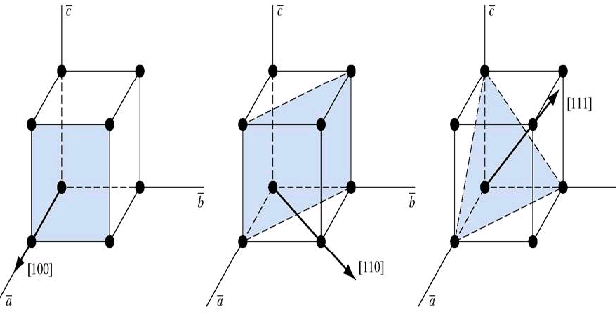
On repère ici Les plans [100],[110] et [111].
Nous verrons l'importance de ces plans dans la diffraction et pour l'observation au microscope.

2 - Conditions de diffraction

Diffraction d´électrons par des plans cristallins

Quand on envoie une onde sur un cristal, il y a un phénomène de diffraction. L´angle entre l´onde diffractée et le plan cristallin est égal à l´angle d'incidence. Considérons maintenant des rayons se réfléchissant sur des plans atomiques successifs d´un cristal séparé par la distance d. Pour observer une intensité diffractée dans la direction teta il faut que les interférences entre les rayons successifs soient constructives, c´est-à-dire que le déphasage entre les rayons successifs doit être multiple de 2p. Ceci revient à dire que la différence de marche entre deux rayons successifs (la différence de longueur de trajet) doit être un multiple de leur longueur d?onde (lambda). On a alors la relation de Bragg (avec n entier naturel non nul)

2.d.sin(teta)=n.lambda

Or un cristal n'est jamais parfait. Il exite des dislocations, c'est à dire un défaut linéaire correspondant à une discontinuité dans l'organisation de la structure cristalline.

Exemple de dislocation cristalline

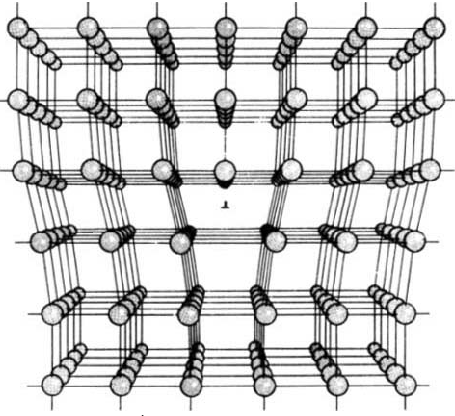
Ainsi, la déformation de la maille cristalline autour de la dislocation change les conditions de diffraction des plans cristallins présents autour du coeur de la dislocation. Ce sont ces déformations qui sont à l'origine du contraste en Haute Résolution

Remarque :

Cette relation montre bien que pour observer une diffraction d´un réseau cristallin, il faut que la longueur d´onde du rayonnement utilisé soit inférieure aux distances interatomiques.

3 - Facteur de structure

L'observation en microscopie électronique est basée sur les interférences constructives entre les ondes : l'étude des propriétés structurales d'un échantillon se fait donc à partir de l'intensité lumineuse locale de l'échantillon. On introduit donc un facteur appelé facteur de structure F :

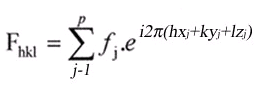
* j représente l'espèce chimique * f représente le facteur de diffusion atomique
* x,y,z la position des noeuds où sont situés les atomes de l'espèce j
* [h,k,l] représente les coordonnées d'un plan cristallin.

Ce facteur varie donc d'un plan cristallin à un autre et l'intensité lumineuse est proportionnelle à ce facteur au carré. C'est donc lui qui va permettre de déterminer la structure et la composition en Indium dans l'échantillon.

CALCUL DU FACTEUR DE STRUCTURE DE InGaAs

Maille de GaAs

On a donc ici un atome de As en (000)et un atome de Ga en (1/4,1/4,1/4).
Quand on ajoute de l'Indium, les atomes d'indium viennent remplacer certains atomes de Gallium. Si on note x la composition en Indium (x compris entre 0 et 1), on trouve alors comme facteur de structure pour une maille de InGaAs :