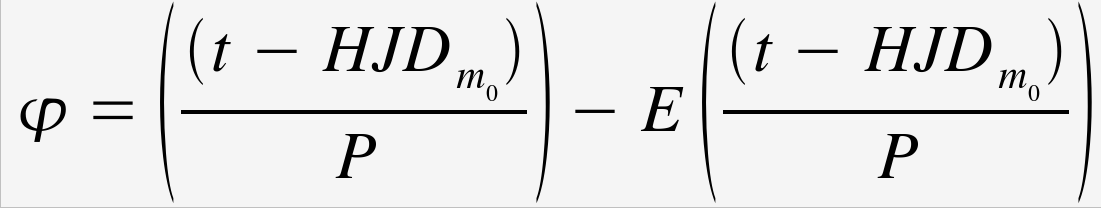 [3]
[3]Il existe deux types d'étoiles : celles dont la magnitude apparente est constante et celles dont la magnitude apparente varie. Pour ces dernières, les variations sont généralement périodiques. Un bon outil pour l'étude de ces étoiles est la construction de courbes de lumières. Elles représentent les variations de la magnitude apparente en fonction du temps. Toutefois, il est nécessaire de définir certains concepts pour la tracer convenablement.
Tout d'abord, il faut construire un système de comptage des jours. En effet, l'année civile commence le 1er janvier - jour 1 - et s'achève le 31 décembre - jour 365 ou 366 - puis repart à 1 l'année suivante. Donc les jours ne sont pas définis de façon unique et dépendent de l'année (si elle est bissextile ou non). Par conséquent, pour faire référence à un phénomène stellaire, on ne peut pas se baser sur cette numérotation. Pour cela, l'astronome Julien a proposé de compter les jours de façon continue : ainsi à 365, on continue avec 366, etc. On note H.J.D. (Heliocentric Julian Day) le Jour Julien Héliocentrique. Le jour Julien dure 24 h, il commence à midi T.U. (temps universel), c'est-à-dire 13h en France l'hiver et 14h l'été. Il permet de construire les éphémérides ; une éphéméride est relative à une étoile donnée et fournit sa période de pulsation et un Jour Julien de référence (qui correspond au minimum ou au maximum de magnitude). Elles sont mises à jour régulièrement.
Cependant, l'observation de l'étoile ne se fait que de nuit. Donc si la période de pulsation excède la durée de la nuit, il faut interrompre la mesure et recommencer la nuit suivante ; d'où des lacunes dans la courbe de lumière. Des observations successives permettent donc d'obtenir différents morceaux de la courbe à différentes dates. Or la magnitude de l'étoile varie périodiquement. Il faut donc ramener tous les bouts de courbe sur une période : c'est le compositage. Afin de réaliser cette opération, on a besoin d'introduire la notion de phase. On définit la phase φ par :
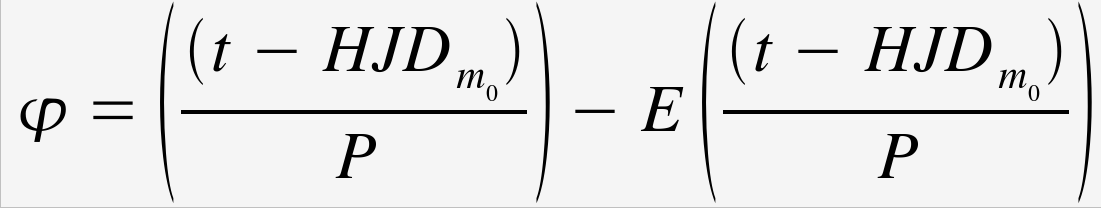 [3]
[3]où E est la fonction partie entière, HJDm0 est un jour Julien de référence et P la période de pulsation (ces deux données sont fournies par les éphémérides). La phase est donc un nombre compris entre 0 et 1. Selon les conventions, on peut avoir en 0 (et en 1) le maximum ou le minimum de magnitude.
La courbe de lumière est, en fait, un graphe donnant la magnitude apparente en fonction de la phase.
Remarque :
on peut se servir de satellites spatiaux (HIPPARCOS, lancé le 18 août 1989 par Ariane) pour observer en continu. Le satellite CoRot a été lancé récemment (le 27 décembre 2006) pour mesurer la rotation et la convection de certaines étoiles. Il donnera des résultats très attendus d'ici deux ans. Une autre solution moins onéreuse est d'observer en Antarctique où la nuit dure 6 mois. Cette technique permet de pouvoir changer le champ d'observation, contrairement aux satellites. De plus, les réparations sur les satellites sont difficilement réalisables et chères.Il existe une relation liant la période de pulsation d'une étoile et sa magnitude absolue : c'est la relation période-luminosité. Elle est donnée par :
où M est la magnitude absolue et P la période. Les coefficients a et b ont été trouvés expérimentalement puis confirmés par un modèle théorique. Voici les valeurs de a et de b pour certains types d'étoiles variables :
La relation période - luminosité ne peut être écrite que pour les RR Lyrae, les Céphéides classiques, et les W Virginis (car elles ont une période très régulière).
Pour avoir la distance de l'étoile par rapport au Soleil on utilise la formule du module des distances :
Remarque :
le télescope HUBBLE a aussi servi pour étudier la relation période-luminosité.