Loi semi circulaire
Comme nous le dit le théorème de Wigner la densité des valeurs propres une matrice de taille infinie converge.
Ainsi en simulant numériquement une telle densité on obtient une densité en demi cercle (car la simulation donnera quelque chose de fini).
Le but de cette partie est de trouver, pour une matrice, un compromis entre le temps de calcul machine et la possibilite de définir le régime uniforme
dans la densité des valeurs propres.
Une fois la taille de cette matrice trouvée on pourra en générer un grand nombre en se placant a chaque fois dans la partie uniforme de la loi
semi circulaire (approche statistique).
Matrice 300x300
 Nous avons ici, un temps de calcul correct ( environ 2 minutes ) et l'apparition du comportement constant prédit par Wigner.
Matrice 900x900
Nous avons ici, un temps de calcul correct ( environ 2 minutes ) et l'apparition du comportement constant prédit par Wigner.
Matrice 900x900
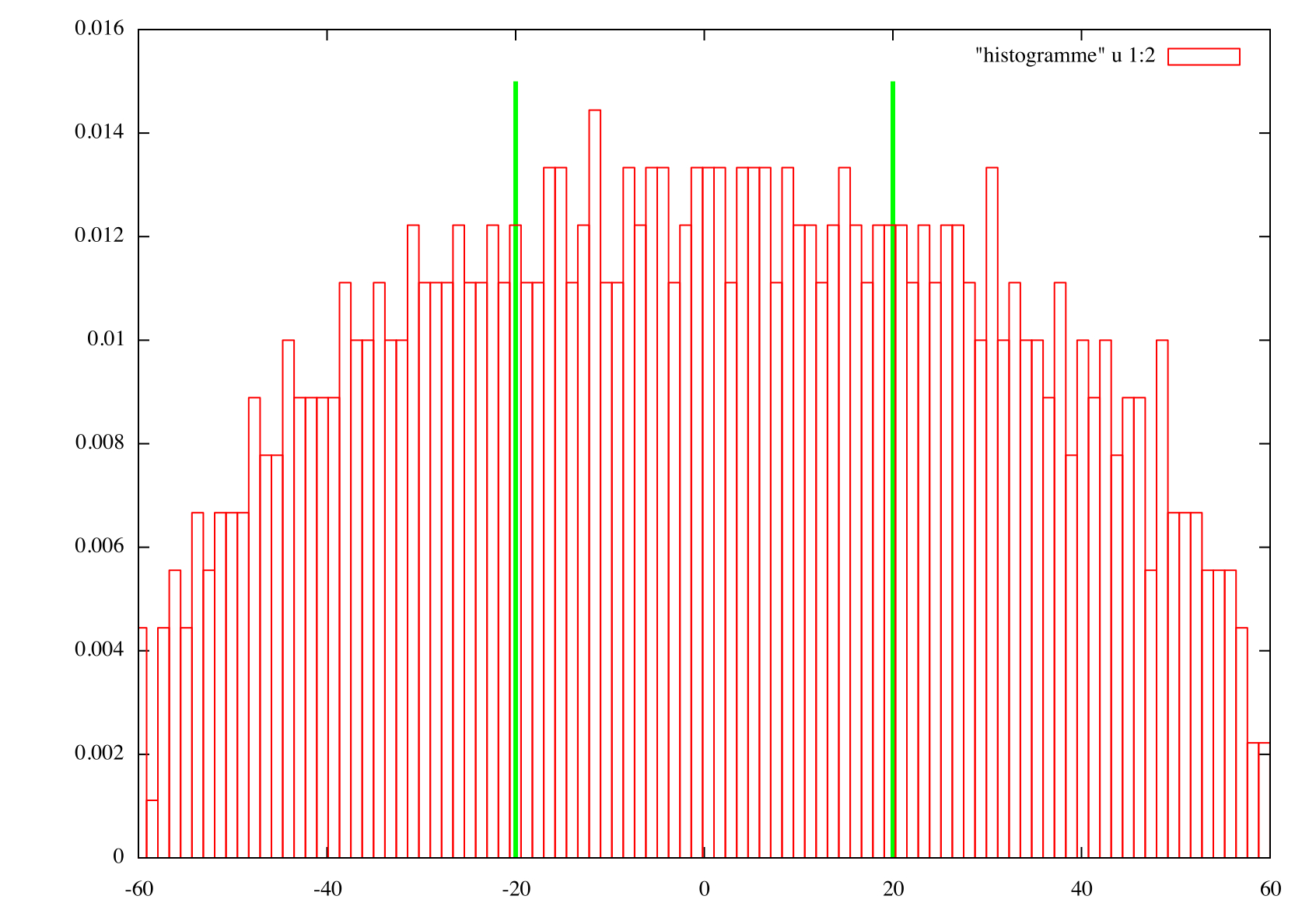 Le temps de calcul est trop long ( supérieur à 5 minutes ) pour le nombre de matrices que nous allons générer. Cependant
nous visualisons mieux dans ce cas la partie constante de la distribution.
En complément, on peut également réaliser le redressement de spectre à partir du nombre cumulé de valeurs propres (modes),
en sélectionnant la partie linéaire de la courbe.
On le représente pour une matrice de taille 300 :
Le temps de calcul est trop long ( supérieur à 5 minutes ) pour le nombre de matrices que nous allons générer. Cependant
nous visualisons mieux dans ce cas la partie constante de la distribution.
En complément, on peut également réaliser le redressement de spectre à partir du nombre cumulé de valeurs propres (modes),
en sélectionnant la partie linéaire de la courbe.
On le représente pour une matrice de taille 300 :
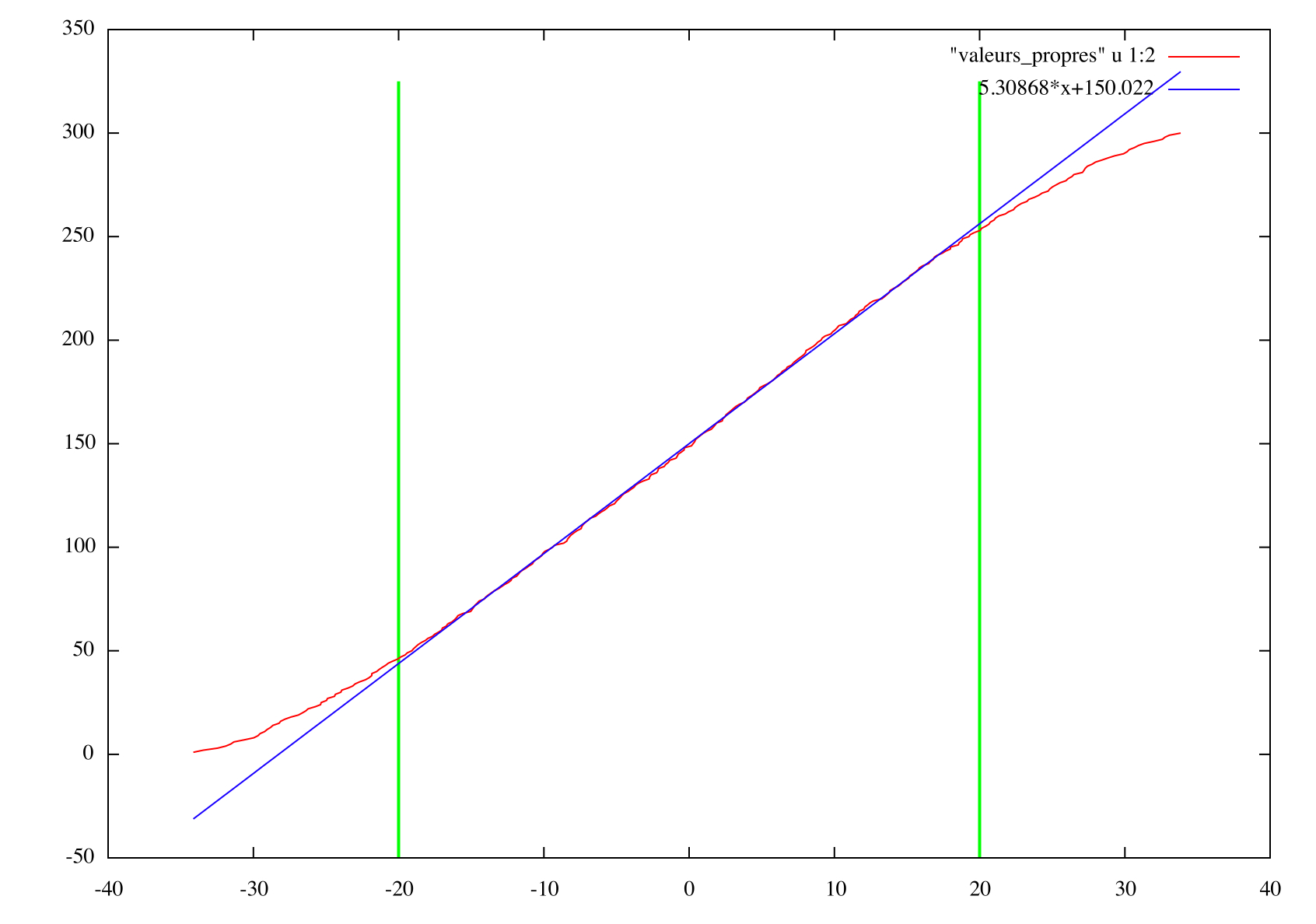 En prenant en compte les 2 critères de sélection précedents, on choisit de faire notre simulation avec
des matrices de taille 300*300 qui nous paraissent être un bon compromis entre temps de calcul et partie centrale constante.
On prend 20 comme valeur seuil pour les valeurs propres.
En prenant en compte les 2 critères de sélection précedents, on choisit de faire notre simulation avec
des matrices de taille 300*300 qui nous paraissent être un bon compromis entre temps de calcul et partie centrale constante.
On prend 20 comme valeur seuil pour les valeurs propres.