INTRODUCTION :

Il est aussi possible de créer un équilibre stable de toute pièce avec des petites oscillations à haute fréquence appliquées à la base du pendule, le tout sans aucun asservissement, comme nous allons le voir dans ce paragraphe.
THÉORIE :
Considérons un pendule soumis à une force dérivée d'un potentiel ainsi qu'à un forçage f.
Le forçage sera périodique :
Le mouvement du pendule peut se décomposer comme suit :






Ré-injectons notre nouvelle fonction position pour trouver :
(1)
(2)
Nous trouvons dans cette équation à la fois des termes décrivant les mouvements doux et des termes décrivant les mouvements oscillatoires rapides que l'on peut évidemment séparer en deux équations distinctes. Pour les termes d'oscillations rapides nous trouvons :





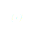
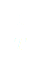








(3)

(4)


(5)
Qui peut aussi s'écrire :
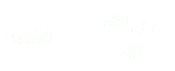
(7)
Où "l'énergie potentielle effective" est définie par :

En comparant cette expression avec l'équation (4), nous voyons que le terme ajouté à U est simplement l'énergie cinétique du mouvement oscillatoire rapide :

(8)
Nous constatons donc que le mouvement du pendule moyenné "au-dessus" d'une oscillation est le même que si le potentiel U était augmenté par une quantité constante proportionnelle au carré de l'amplitude des oscillations.
APPLICATION À NOTRE SYSTÈME :
Nous venons de voir ce qu'est l'énergie potentielle effective d'un pendule subissant un forçage périodique de haute fréquence.
Nous pouvons donc étudier la stabilité d'un tel pendule.
Soit dans notre cas:


(9)

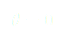


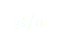


(10)
En dérivant l'équation (10), il vient :

(11)






Nous pouvons maintenant étudier la stabilité de ces deux points en dérivant une seconde fois l'équation (10) :

(12)





NB : Tous l’aspect théorique de cette page a été amplement inspiré par le livre “Course of Theorical Physics - Volume 1” de L.D. LANDEAU et E.M. LIFSHITZ