Propriétés des singularités

Une fois les résultats expérimentaux améliorés, nous avons pu nous intéresser à une zone particulière du champ observé : la singularité. En fait, la singularité proprement dite est un point particulier du champ d'interférences qui a à la fois une partie réelle et une partie immaginaire nulle et, à forciori, une phase non définie. Cependant, la zone présente autour d'une singularité présente elle aussi des carractéristiques bien particulières. Nous avons mis en évidence un certain nombre de ces carractéristiques qui ne sont visibles que si on s'approche suffisament près à l'aide de notre programme d'interpolation qui nous a permis de faire un zoom sur cette partie particulière du champ.

Les propriétés : Interessons-nous tout d'abord aux propriétés des singularités qui nous sont données par la théorie :
1. Propriétés de la phase : On remarque que les lignes d'équiphases sont des demi-droites qui se rejoignent au niveau de la singularité. En suivant une demi-droite, nous verrions, lors de la traversée de la singularité, la phase augmenter (ou diminuer) brutalement de Pi. Si nous nous déplacions le long d'un cercle suffisament petit centré sur la singularité, nous verrions la phase varier continuement de telle manière que, une fois retourné au point de départ, elle aurait augmenté (ou diminué) de 2 Pi : le sens de parcours qui permet de voir la phase augmenter définit le signe (positif ou négatif) de la singularité. Nous choisissons de définir le sens positif comme étant le sens horaire. Cela revient à dire que la circulation de la phase le long du cercle vaut 2 Pi. (Notons qu'il existe aussi des singularités autour desquelles la circulation de la phase vaut un multiple de 2 Pi mais aucune singularité de ce type n'est présente dans l'expérience que nous avons étudiée.)
2. propriétés de l'intensité : L'intensité est définie comme étant la somme des carrés de la partie réelle et de la partie imaginaire. Les lignes d'équiintensité sont des ellipses centrées autour de la singularité
3. propriétés du courant : Le courant est défini comme suit : abs(E*.grad(E)) : les lignes d'équicourant sont des cercles.

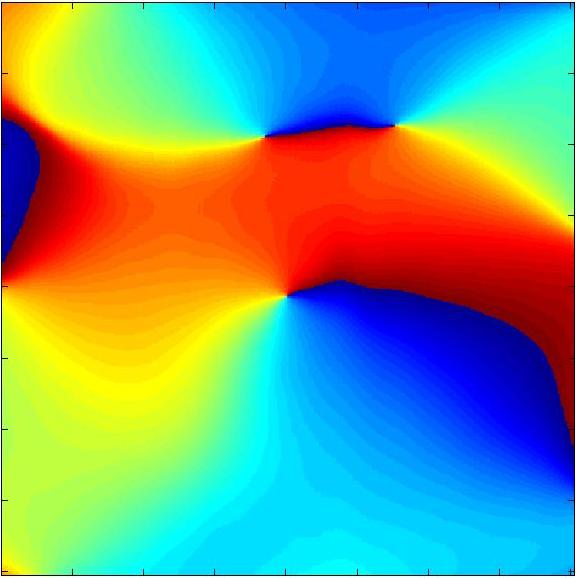
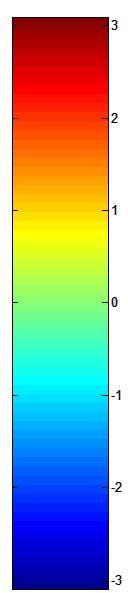
Photo du montage :
Zoom sur trois singularités proches