Suivi de la singularité en fonction de la fréquence

Nous nous intéressons maintenant au suivi des singularités en fréquence. Nous avons en effet travaillé jusqu'à présent à fréquence fixe, et nous avons observé qu'il y avait de nombreuses singularités positives et négatives. La question que l'on se pose maintenant est : quel est le trajet d'une singularité lorsque l'on se déplace en fréquence, et quel est son comportement avec les autres singularités ?

Pour se faire nous avons programmé à l'aide de Matlab, un algorithme qui permet de suivre une singularité.
Il faut noter la chose suivant avant de chercher à suivre une singularité : nous remarquons que les singularités disparaissent au cours de l'évolution en fréquence, en fait chaque singularité est amenée à fusionner avec une autre du signe opposé.

Nous avons d'abord programmé de la manière suivante:

Le programme cherche toutes les singularités sur la matrice de phase de la première fréquence étudiée.
Le programme considère ensuite la première singularité positive qu'il trouve, c'est celle-ci qu'il suivra dans un premier temps.
Afin de suivre la singularité positive on considère qu'elle s'est déplacée au plus d'une distance d d'une fréquence à l'autre et on regarde dans la matrice de la fréquence suivante s'il y a une singularité de même signe dans une "case" de côté 2d centrée sur l'ancienne position de la singularité positive, si c'est le cas on considère que c'est la nouvelle position de la singularité.
Si il n'y a pas de singularité de même signe à la fréquence suivante, c'est que celle-ci a fusionné avec une autre de signe opposé.
Le programme repart donc de la dernière position connue de la singularité et balaye le champ des fréquences en sens inverse à la recherche d'une singularité de signe opposé qui serait contenue dans une case de côté 2d comme précédement.
L'algorithme peut être renouvellé de nombreuses fois et le programme garde en mémoire les positions des singularités ainsi que leur signe ce qui permet de tracer les trajectoires des singularités en fonctions de la fréquence.

Nous avons donc commencé par programmer comme précédement mais nous nous sommmes rapidement rendu compte que le critère de sélections de nos singularités dans une case de côtés 2d n'était pas efficace car il fallait changer l'échelle à chaque fois que l'on considérait une nouvelle case, ce qui compliquait inutilement les calculs.
Il présentait aussi un autre inconvénient qui était celui de prendre le risque de considérer deux singularités de même signe situées dans la même case et de confondre les trajectoires.
Pour toutes ces raisons nous avons abandonné ce critère et modifié l'algorithme.
Dans le nouveau programme, on sélectionne donc la première singularité positive comme précedement mais pour la rechercher à la fréquence suivante on ne se sert plus de cases mais on préfère détecter toutes les singularités à la fréquences suivante et choisir celle de même signe qui est la plus proche de l'ancienne position à condition que l'écart entre les deux positions n'est pas supérieur à une condition limite définie empiriquement. Si aucune singularité de même signe ne respecte cette condition alors on revient en arrière comme précédement et on cherche une singularité de signe opposé avec le même critère.

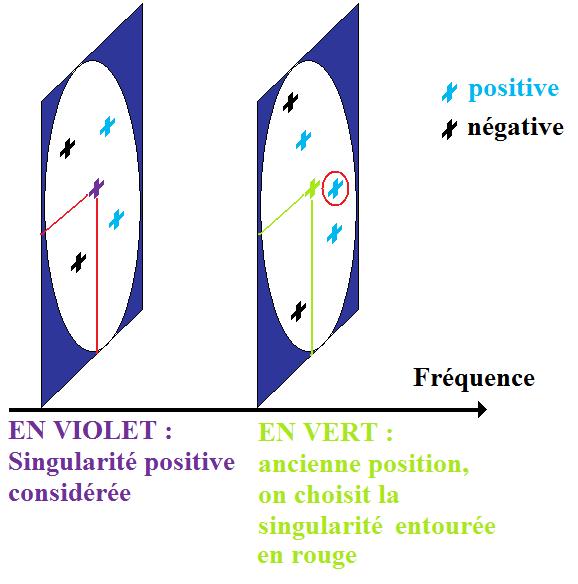
Afin de pouvoir contrôler ce que l'on fait on crée deux programmes semi-automatiques l'un pour suivre les singularités dans le sens des fréquences croissantes, l'autres dans le sens des fréquences décroissantes. On affiche ensuite en trois dimensions en temps réel point par point les positions des singularité positives et négatives ce qui nous permet de contrôler l'évolution du traçage.

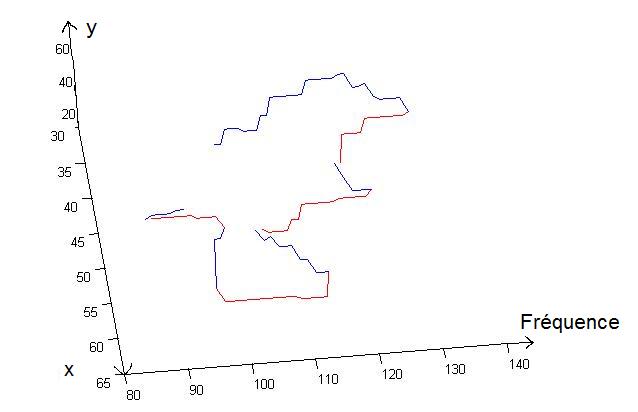
Suivi en fonction de la fréquence :
en bleu, la singularité est positive
en rouge, la singularité est négative.
On remarque sur le tracet que toutes les singularités sont reliées, elles ne forment qu'un seul long "fil" alternant singularités positives et singularités négatives qui s'annulent mutuellement. En effet, si on observe deux singularités de signes opposées à une même fréquence elles vont finir par fusionner soit lorsque la fréquence augmente soit lorsqu'elle diminue.