Effet Zeeman

Dans le modèle classique, on visualise une charge électronique liée au noyau par un oscillateur harmonique. La fréquence ν₀ de l'oscillateur correspond à la fréquence d'une ligne d'émission ou d'absorption. Le phénomène d'absorption se produit quand l'oscillateur est excité par le champ électrique d'un rayon incident. Une partie de l'énergie du rayon incident est transférée à l'oscillateur. L'inverse se produit lors du processus d'émission : l'énergie de l'oscillateur est rayonnée par un photon.

Si l'oscillateur est excité aléatoirement, par exemple lors de collisions, le rayonnement est émis dans des directions aléatoires et est non polarisé. Mais en la présence du champ magnétique externe, on peut avoir une émission polarisée.

Pour une explication plus complète, il faut considérer la mécanique quantique..
Les niveaux d'énergie sont discrétisés et les électrons peuvent les occuper. Les raies spectrales d'absorption correspondent aux fréquences qui permettent d'effectuer le passage d'un électron d'un niveau d'énergie (c'est à dire d'un état quantique) à un autre, en obéissant aux règles de transition :
Δn ≠ 0, Δl = ± 1 Δm= ±1, 0

En l'absence de champ magnétique, les niveaux d'énergie des électrons de la même sous-niveau l sont dégénérés (ils ont la même énergie)..
Le vecteur du moment magnétique de l'électron peut prendre n'importe quelle direction sans que l'énergie du système ne varie. Ce n'est plus le cas en présence d'un champ magnétique. L'énergie de l'électron va dépendre de l'alignement de son moment magnétique avec la direction du champ. Il n'y a alors plus de symétrie sphérique et donc de dégénérescence des niveaux.

Des sous-niveau s à p (exemple représenté ici), il va donc y avoir trois transitions possibles d'énergies différentes et donc le spectre d'absorption nous montrera non plus une mais trois raies en la présence d'un champ magnétique. Ceci est aussi valable pour les transitions entre d'autres sous-couches car, comme nous l'avons vu précédemment, lors d'une transition électronique, Δm= ±1 ou 0..
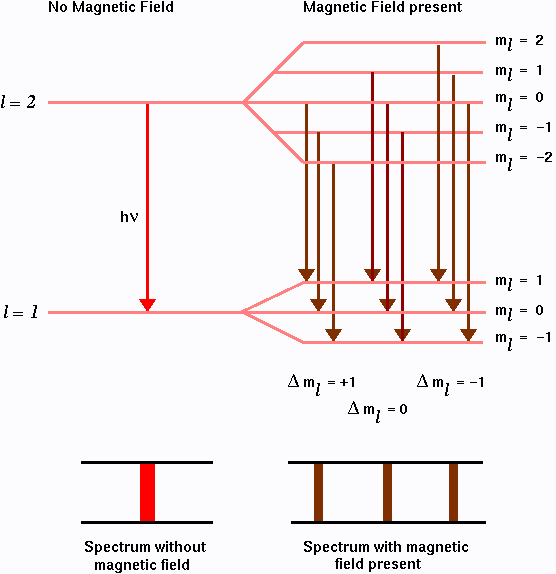
Si en l'absence d'un champ, le spectre comportait une raie d'absorption à la fréquence ν₀, le champ conduira à l'apparition de nouvelles raies aux fréquences ν₀+ν_L et ν₀-ν_L où ν_L est la fréquence de Larmor.

Ainsi le triplement des raies d'absorption sur le spectre en un point du disque solaire y signale la présence d'un champ magnétique. On peut, en mesurant l'écart en fréquence entre les raies, déduire la valeur de ce champ.
Cependant, l'effet Zeeman n'est perceptible que pour des champs magnétiques très élevés. Il faut en effet tenir compte de la largeur des raies d'absorption qui est due à l'effet Doppler. Les particules sont en mouvement brownien constant d'une vitesse moyenne dépendant de la température du milieu. Si le magnétisme n'est pas assez important, les raies ne seront pas suffisamment espacées pour être différenciées.
A la surface du soleil, le champ magnétique peut être suffisamment important (par exemple dans des tâches solaires) pour avoir un effet Zeeman perceptible sur le spectre.

Δv_D = ν₀.w/c.
w = √(3kT/m) vélocité thermique.
Pour pouvoir voir la séparation Zeeman des raies, il faut que le ratio ν_L/Δv_D soit nettement supérieur à 1.


L'effet Zeeman s'avère pratique pour mesurer les champs forts, notamment à l'intérieur des tâches solaires. Les importants mouvements de convection déplacent de grandes quantités de plasma induisant un très intense champ magnétique (1000 à 2000 Gauss).

Pour les petits mouvements de convection en surface, le champ magnétique généré est trop faible pour être mesuré par cette méthode. On utilise donc l'effet Hanle.