Analogie entre une membrane et des oscillateurs
Description d’une membrane
Comme beaucoup de systèmes physiques, le mouvement de la membrane d’un tambourin soumise à une excitation peut être décrit par des systèmes oscillants.
Au cours de notre étude, nous avons ainsi rencontré deux sortes de systèmes oscillants :
- Un couplage d’oscillateurs harmoniques libres (amortis et non amortis) pour décrire les deux réponses impulsionnelles (théorique et expérimentale) ;
- Une superposition d’oscillateurs harmoniques forcés et amortis, décrivant la réponse forcée de la membrane (partie Le son en image).
Nous vous proposons donc d’étudier ces deux situations. Nous pourrons ainsi en déduire la forme des résonances d’une membrane.
Réponses libres de la membrane
Durant notre projet, nous avons simulé l’évolution de la membrane soumise à une excitation brève et localisée, c'est-à-dire une réponse impulsionnelle théorique, et effectué l’expérience correspondante.
La déformation de la membrane, due à une excitation, correspond alors à l'évolution temporelle d'une superposition de ses modes propres.
Or, comme nous l’avons vu dans la partie Théorie sur les ondes, un mode propre de la membrane est caractérisé par l’établissement d’une onde stationnaire à sa surface. L’onde effectue alors des oscillations sinusoïdales de période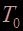 
autour de la position au repos de la membrane 
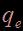. La seule variable qui décrit le système à un degré de liberté est alors l’élongation verticale de la membrane.
L’évolution temporelle d’un mode après une excitation brève peut donc être comparée à celle d’un oscillateur harmonique libre.
Par conséquent, l'évolution temporelle d'une superposition de ses modes propres peut être comparée à celle d’un couplage d’oscillateurs harmoniques libres !
La différence entre les deux réponses impulsionnelles vient des considérations énergétiques :
- Pour la simulation, nous n’avons pas tenu compte du milieu extérieur. Il n’y a ni couplage avec le contour du tambourin, ni couplage avec l’air. Le système ne dissipe aucune énergie. Par analogie, il s’agit d’un couplage d’oscillateurs libres non amortis ;
-
Pour l’expérience en revanche, nous n’avons pas pu nous affranchir des dissipations d’énergie mécanique ou par rayonnement. Nous pouvons donc décrire le système comme un couplage d’oscillateurs libres amortis.
En étudiant le mouvement d’un oscillateur harmonique libre, nous pouvons donc déterminer la forme générale d’une résonance associée à un mode quelconque de la membrane. C’est l’objet du paragraphe qui suit.
Remarque : nous effectuons l’étude générale d’un oscillateur amorti, l’oscillateur non amorti correspondant à un cas particulier où les forces de frottements sont négligeables.
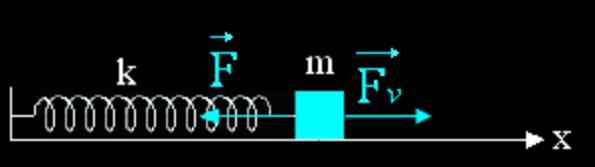
Fig.1 – Exemple d’oscillateur harmonique libre
Prenons l’exemple d’une masse m soumise à la force de rappel F d’un ressort (de constante de raideur k), et à une force de frottement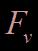 
de type visqueuse (exemple : résistance de l’air).
L’équation fondamentale de la dynamique s’écrit alors :
Suivant l’axe x,
Finalement,
Avec :
- 
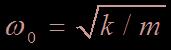la pulsation de l’oscillateur harmonique non amorti ;
- 
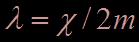le coefficient d’amortissement (nul pour un oscillateur non amorti).
Les solutions générales de cette équation différentielle sont de la forme :
Comme nous l’avons vu dans la partie généralités, il existe alors deux régimes : le pseudo périodique et l’apériodique. L’amortissement provoqué par l’air n’est pas suffisamment important pour entraîner un régime apériodique. Nous considérons donc un amortissement faible, où
Dans cette limite,
Avec
- a une constante et 
le déphasage, tous deux définis par les conditions initiales ;
- ω la pulsation de l’oscillateur, telle que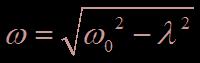 
.
Si l’on effectue une analyse de Fourier, le module carré de l’amplitude des oscillations dans le domaine fréquentiel est donné par :
Soit
Avec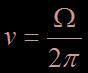 
la fréquence (variable conjuguée du temps).
On note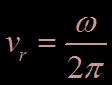 
.
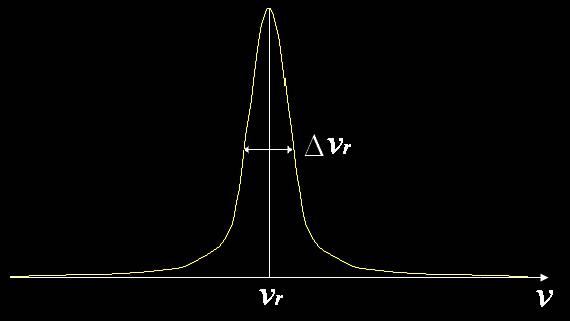
Fig.2 – Module carré de l’amplitude des oscillations dans le domaine fréquentiel
Ainsi,
Avec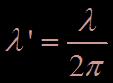 
et α un coefficient multiplicatif.
Une résonance a donc la forme d’une lorentzienne,
centrée en 
et de largeur à mi-hauteur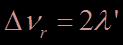 
.
En conclusion, si l’on trace le spectre en fréquence d’un oscillateur harmonique amorti, nous obtenons la figure 2.
Par analogie, la forme générale d’une résonance associée à un mode propre de la membrane est une lorentzienne centrée sur la fréquence de résonance correspondante.
Considérons maintenant un couplage d’oscillateurs harmoniques libres. Le spectre correspondant est donc une succession de lorentziennes centrées sur différentes fréquences.
En traçant le spectre correspondant à l’évolution temporelle de la membrane après excitation, nous obtenons donc une succession de lorentziennes centrées sur les fréquences de résonance de la membrane :
Avec
- n le nombre de modes que l’on considère ;
- 
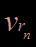la nième fréquence propre ;
- 
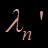représente le coefficient d’amortissement, qui varie suivant les modes. En effet, les pertes d’énergie des modes ne sont pas toutes identiques.
Remarques : dans le cas de la réponse impulsionnelle théorique (simulation), le système est décrit par un couplage d’oscillateurs harmoniques non amortis. Le raisonnement est le même en considérant le coefficient λ nul. Les résonances correspondent donc à des lorentziennes de largeur à mi-hauteur nulle, en somme, des deltas de Dirac.
Grâce à une analogie simple avec des oscillateurs harmoniques, nous connaissons l’allure du spectre de la réponse libre d’une membrane, ainsi que la forme de ses résonances.
Réponse forcée de la membrane
Nous pouvons maintenant nous intéresser à la réponse forcée de la membrane : l’étude est semblable à celle de la réponse libre. En appliquant une force extérieure à la membrane, on la « contraint » à osciller avec une certaine fréquence, et on excite tous ses modes propres. Sa réponse est alors semblable à celle de la superposition de plusieurs oscillateurs forcés. De plus, il existe lors de cette expérience des pertes d’énergie. Nous pouvons donc faire l’analogie entre la membrane et une superposition d’oscillateurs amortis forcés.
Nous allons donc nous intéresser dans un premier temps à la réponse en fréquence d’un oscillateur amorti forcé.
La loi fondamentale de la dynamique est la même que pour l’oscillateur amorti libre, avec un terme supplémentaire, provenant de la force extérieure appliquée à la membrane. Celle-ci correspond, dans notre expérience, à un signal électrique sinusoïdal délivré par un générateur basse fréquence, et transformé en signal sonore par un haut-parleur. On note cette force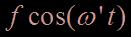 
.
Dans ce cas-là, la loi fondamentale de la dynamique s’écrit :
La solution de cette équation différentielle est composée d’une solution stationnaire et d’une solution décrivant le mouvement transitoire de l’oscillateur après déclenchement de la force extérieure. Si l’on s’intéresse seulement au régime permanent, la solution stationnaire est de la forme :
Avec
- ω’ la pulsation de l’oscillateur ;
- b une constante ;
- φ le déphasage.
Lorsque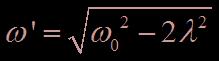 
on observe une résonance de l’oscillateur.
De plus, le module carré de l’amplitude s’écrit, comme dans le cas d’un oscillateur libre amorti :
Avec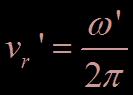 
.
Par analogie, la forme générale d’une résonance associée à un mode propre de la membrane est là encore une lorentzienne centrée sur la fréquence de résonance correspondante et de largeur à mi-hauteur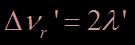 
.
Si l’on considère maintenant la réponse globale de la membrane à une excitation forcée, nous pouvons faire l’analogie avec une superposition de plusieurs oscillateurs amortis forcés de pulsations différentes.
Le module carré de l’amplitude s’écrit comme celui de la réponse libre :
Mais il y a toutefois une différence majeure : on force la membrane à vibrer à une fréquence précise. Lorsque cette fréquence est très proche d’une des fréquences de résonance,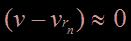 
.
Dans la somme de la formule (17), il y a donc un terme qui domine sur les autres et qui contribue à la valeur de A². Ceci explique que lors de la réponse forcée, nous n’observons qu’une seule et unique résonance.
Ce résultat est valable dans la limite où l’on considère des résonances bien séparées les unes des autres, c'est-à-dire lorsqu’elles ne sont pas trop larges. Il faut donc pour cela que l’amortissement du système (pertes d’énergie) soit faible.
Remarque : nous pouvons constater que la pulsation résonante de l’oscillateur amorti forcé diffère de celle de l’oscillateur amorti libre : elle est plus faible.
Dans la limite où l’amortissement est faible devant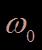 
, la fréquence de résonance de l’oscillateur libre est :
Et celle de l’oscillateur forcé :
La différence de fréquence est de l’ordre de
Elle est donc négligeable si l’on reste dans la limite d’un amortissement faible.
Cette étude nous a permis de mettre en évidence une différence entre les fréquences de résonances de la membrane lorsqu’elle évolue librement (réponse impulsionnelle) et lorsqu’elle soumise à une excitation périodique (réponse forcée).
