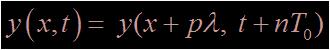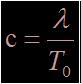Ondes mécaniques progressives
Dans la nature, les phénomènes ondulatoires se manifestent sous plusieurs formes, comme par exemple les vagues sur un lac, les ondes électromagnétiques, les tremblements de terre, la vibration de cordes sur un instrument de musique, la vibration d’une membrane sur un tambour, etc…
Lorsqu’il s’agit de propagation d’une perturbation dans un milieu matériel sans transport de matière, on parle d’onde mécanique progressive : elle se propage de proche en proche, avec un transfert d’énergie.
Il en existe deux sortes :
- Les ondes longitudinales provoquant une perturbation dont la direction est parallèle à la direction de propagation de l’onde (exemple : la propagation d’une onde sur un ressort).
- Les ondes transverses provoquant une perturbation dont la direction est perpendiculaire à la direction de propagation de l'onde (exemple : la propagation d'une onde à la surface d'une membrane).
Prenons l’exemple 1D d’une corde vibrante, que nous pourrons généraliser au cas 2D d’une membrane circulaire.
Comme le montre le schéma ci-dessous, lorsqu’on provoque une déformation de la corde, la perturbation se propage de proche en proche dans la direction horizontale alors que les points de la corde se déplacent verticalement (d'abord de bas en haut puis de haut en bas) :
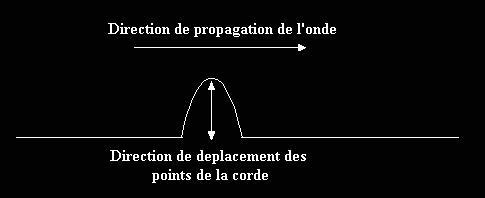
Fig.1 - Déformation d’une corde
Il s’agit donc d’une onde transverse, comme dans le cas d’une membrane.
Considérons maintenant le cas où une source S impose une perturbation périodique sinusoïdale au milieu matériel. Nous constatons qu’une onde progressive périodique se propage sur la corde. Celle-ci est caractérisée par une double périodicité :
- Période temporelle : il existe une périodicité dans le mouvement de chaque point de la corde, notée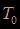 
. Ceci signifie que l’intervalle de temps minimal séparant deux instants où un point de la corde a le même mouvement correspond à une période :
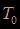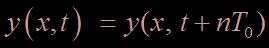 avec n un entier et y l'élongation verticale de la corde
|
(1) |
- Périodicité spatiale : l'aspect de la corde à un instant donné est une fonction sinusoïdale. Cette fonction a pour période λ, la longueur d’onde, correspondant à la distance séparant deux points consécutifs de la corde ayant au même instant un même mouvement :
De façon générale, pour tout point M d'abscisse x et à tout instant t,
 |
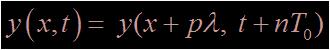(3) |
Sachant que la longueur d'onde correspond à la distance parcourue par l'onde pendant une durée égale à sa période (cf. figure 2), la vitesse de propagation de l’onde est définie par :
 |
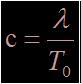(4) |
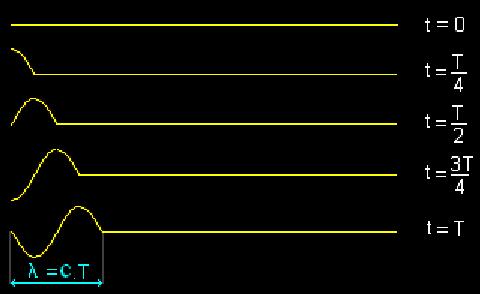
Fig.2 - Relation entre λ et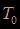
Ondes stationnaires
Considérons maintenant le cas où la corde de longueur L est fixée à ses extrémités. L’onde progressive périodique va se réfléchir et se propager dans la direction opposée à l’onde incidente, puis à nouveau se réfléchir etc… Il en résulte une superposition de plusieurs ondes de mêmes fréquences.
Lorsque ces ondes sont synchrones, la perturbation résultante ne se propage plus ; on parle d’onde stationnaire.
La condition de stationnarité est obtenue lorsque chaque onde se retrouve dans le même état vibratoire en ayant effectué un aller-retour le long de la corde, soit
 |
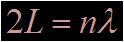(5) |
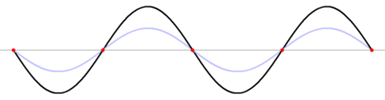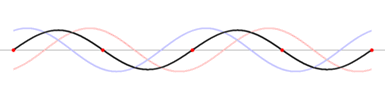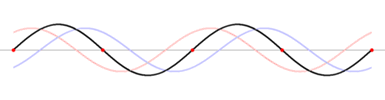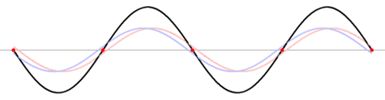
Fig.3 - Simulation d’une onde stationnaire (Wikipédia)
On peut constater que certains points de la corde, appelés des nœuds, sont fixes au cours du temps alors que d’autres, les ventres, sont des maximums de vibrations.
Ainsi, la valeur de n détermine des modes de vibration.
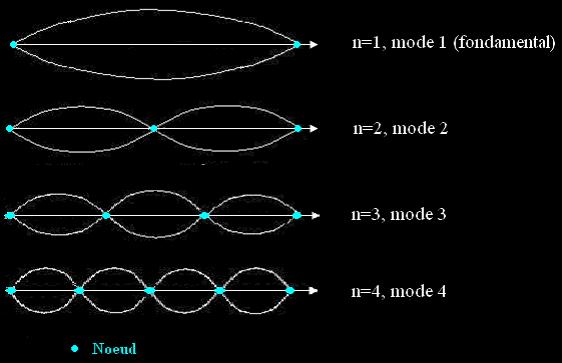
Fig.4 - Allure des 4 premiers modes d’une corde vibrante
La fréquence du mode n est liée au fondamental par la relation
 avec n=1, 2, 3 |
(6) |
Les fréquences des modes sont des multiples de la fréquence fondamentale ; on parle alors d’harmoniques.
Dans le cas d’une membrane circulaire, la propagation des ondes est régie pas les mêmes principes : pour certaines valeurs de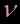 
, une onde stationnaire de plus grande amplitude s’établit à la surface, et caractérise les modes propres de la membrane. Ces fréquences sont appelées fréquences de résonance.
En revanche, les zones où l’amplitude est nulle sont des lignes, radiales ou circulaires, et non des points : on parle de lignes nodales. Les modes ne seront pas caractérisés par un seul indice n, mais par deux indices m et n, l’indice m caractérisant les lignes nodales radiales, et l’indice n caractérisant les lignes nodales circulaires.
Nous nous proposons donc de résoudre de manière analytique le problème de la propagation d’une onde mécanique progressive à la surface d’une membrane circulaire.
Dans un premier temps, nous pouvons établir l’équation d’onde en coordonnées polaires, puis en chercher les solutions stationnaires.
