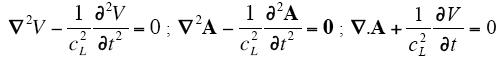
L'observation du rayonnement de Hawking est inenvisageable à l'heure actuelle : il est trop faible pour être mesuré dans le cosmos et la reproduction en laboratoire d'un trou noir est bien évidemment inenvisageable. Il faut donc trouver un autre moyen de prouver son existence par l'expérience. Une des pistes actuelles suivies par les chercheurs est l'utilisation d'analogies.
La propagation des ondes lumineuses est régie par les équations de Maxwell dont on peut tirer les équations d'évolution des potentiels scalaire et vecteur en espace-temps plat de Minkowski (absence de gravitation) :
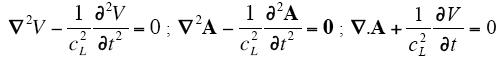
En mécanique des fluides, la propagation des ondes sonores en l'absence d'écoulement à grande échelle est décrite par l'équation de Navier-Stokes et l'équation de conservation de la masse [4]. Elles donnent les équations d'évolution de l'enthalpie massique et de la vitesse du fluide due au son :
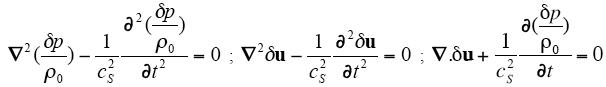
On remarque que ces deux séries d'équations sont très similaires, ce que l'on résumera par le tableau suivant [5] :
| Grandeurs hydrodynamiques | Grandeurs électromagnétiques |
|---|---|
Enthalpie massique p/ρ |
Potentiel scalaire V |
Vitesse u (Impulsion hydrodynamique) |
Potentiel vecteur A (Vecteur électronique, impulsion électromagnétique) |
Vorticité w |
Induction magnétique B |
Vecteur de Lamb l (Accélération de Coriolis) |
Champ électrique E |
Cette analogie s'étend à l'espace-temps courbe en gravitation, ce qui correspond à l'existence d'un écoulement à grande échelle en hydrodynamique.
Quel peut être l' analogue d'un trou noir en hydrodynamique ?
La principale caractéristique d'un trou noir qui nous intéresse est l'existence d'un horizon : la vitesse de libération au sein du trou noir devient supérieure à la vitesse des ondes. L'analogue hydrodynamique d'un champ gravitationnel de relativité générale est un contre-courant.
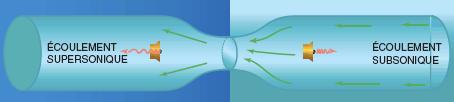
Prenons l'exemple de la tuyère de Laval. Dans la partie de droite, le courant est subsonique : des ondes sonores émises dans cette partie peuvent remonter le courant en subissant un effet Doppler ou descendre dans le même sens que le courant. Dans la partie de gauche, le courant est supersonique : des ondes sonores émises dans cette partie sont entraînées vers l'aval, quelle que soit la direction d'émission. On peut donc considérer la tuyère de Laval comme un trou noir acoustique puisque des ondes peuvent y pénétrer mais pas en sortir. Le col de la tuyère est l'endroit où la vitesse du fluide atteint la vitesse du son : c'est l'horizon de ce trou noir.
Il existe d'autres trous noirs hydrodynamiques : une cascade, la bonde d'un évier, une rivière passant dans un étranglement...

En renversant le temps, un trou noir devient un trou blanc : une région de l'espace où aucune onde ne peut pénétrer. Le jet d'un robinet impactant sur une plaque, ce qu'on appelle un ressaut hydraulique, en est un exemple.
Dans le vide, la relation de dispersion des ondes électromagnétiques est : ω² = k²c²
Par contre, si on s'intéresse plutôt à des ondes de surface, on obtient une relation de dispersion plus compliquée [4] : ω² = gk.tanh(kH)
Lorsque kH<<1, tanh(kH) ≈ kH. Donc la relation de dispersion devient : ω² = gHk². On peut remarquer que les deux relations coïncident.
En introduisant un contre-courant de vitesse moyenne ou typique U, on obtient la relation de dispersion tenant compte de l'effet Doppler :
(ω-kU)² = gk.tanh(kH)
Quand on résout cette relation de dispersion, on peut trouver jusqu'à quatre solutions. Le graphique suivant est la représentation ω = f(k) pour la relation de dispersion des ondes de surface.
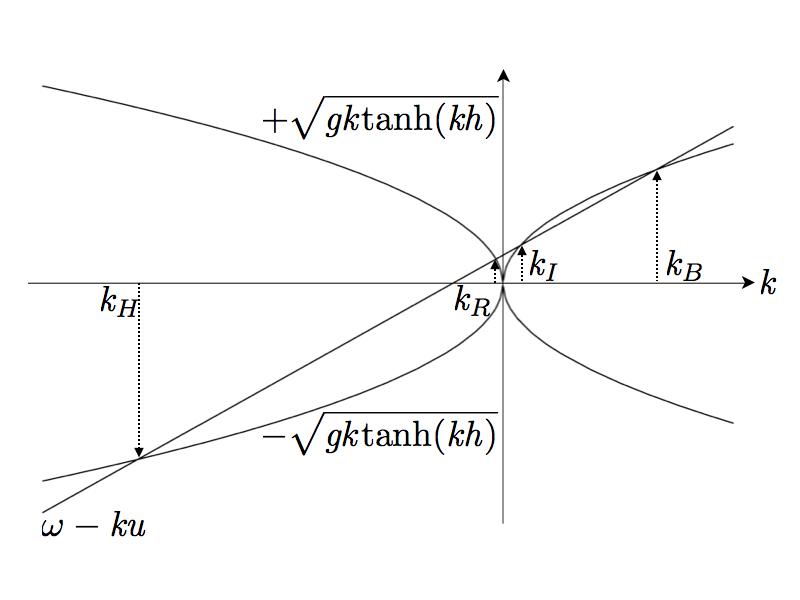
On remarque qu'avec une vitesse du fluide bien choisie, il y a quatre solutions que l'on peut interpréter grâce au signe de leur vitesse de phase (vφ=ω/k) et de leur vitesse de groupe (vg=dω/dk). Sur le graphique, ω est l'ordonnée à l'origine de la droite et les différentes valeurs de k sont aux intersections avec la droite ω-kU. La vitesse de groupe se déduit de l'angle entre la tangente à la courbe et la droite.