
Un trou noir est tellement massif qu'aucun rayonnement ne devrait pouvoir s'en échapper. Pourtant, en 1973, Stephen Hawking a démontré théoriquement l'existence d'un rayonnement que les trous noirs émettraient spontanément. Ce rayonnement est un rayonnement de type corps noir. On peut donc y associer une température, la température de Hawking.

Le diagramme spatio-temporel (r-t) ci-dessus illustre une explication de l’effet Hawking. Dans le vide, il se crée en permanence des paires particule/antiparticule qui s’annihilent au bout d’un temps très court : ce phénomène se nomme la fluctuation quantique du vide. Il est illustré sur le schéma par les flèches oranges. Par contre, il est possible qu’une paire particule/antiparticule se forme de part et d’autre de l’horizon d’un trou noir (en gris) ou de telle manière qu’une des particules puisse échapper au champ gravitationnel tandis que l’autre reste prisonnière. Ceci est illustré par les flèches bleues. On comprend alors qu’il résulte de ce phénomène un flux de particules s’éloignant du trou noir.
Actuellement, certains scientifiques émettent une autre hypothèse : une paire particule/antiparticule se formerait à l'intérieur du trou noir du fait de la fluctuation quantique du vide. L'une des deux resterait alors dans le trou noir tandis que l'autre passerait l'horizon du trou noir par effet tunnel et pourrait ainsi s'échapper et produire le rayonnement de Hawking (interprétation due au prix Nobel de Physique Frank Wilczek).
Cherchons à trouver un ordre de grandeur de la température de Hawking.
Tout d'abord, en physique statistique, l'énergie cinétique d'agitation thermique s'exprime : E = kBT
Ensuite, un photon de lumière de fréquence ν a une énergie : E = hν
On sait aussi que la fréquence d'un onde est liée à sa longueur d'onde par : ν = c/λ
Pour évaluer λ, utilisons les conditions à la Bohr : en considérant une onde qui serait liée à l'horizon du trou noir, sa longueur d'onde serait un multiple de 2πRS. Pour une énergie minimale, on aura λ = 2πRS
On rappelle l'expression du rayon de Schwartzchild (voir la partie I) RS = 2MG/c²
En définitive, on obtient :
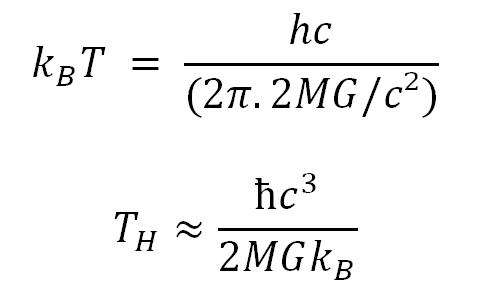
Ce raisonnement très simple amène à une très bonne approximation de la température de Hawking puisque sa valeur exacte est :
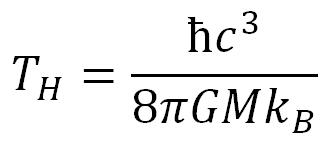
Comme nous l’avons vu dans l’introduction, cette température est extrêmement faible par rapport au fond cosmologique. La détection d'un rayonnement de Hawking spontané est donc, à l'heure actuelle (et probablement pour longtemps), impossible à envisager.