3) Obtention de l’image des couches de GaAs/AlAs en champ noir

a- Protocole

Dans le mode BRIGHT TILT :

-          Choisir une zone du trou où l’épaisseur de l’échantillon est la plus faible possible.

-          S’assurer que la mise au point est correcte et l’axe de zone aussi.

-          Sélectionner le point du cliché de diffraction qui nous intéresse avec le diaphragme, c’est-à-dire le plan selon lequel nous allons observer l’échantillon en champs noir.

-          Se placer dans le mode DARK TILT

-          Placer la tâche sélectionnée au centre de l’écran

    b- Résultats, interprétation ( calcul de facteurs de structure)

Miroir de Bragg en champs noir

            Cette image en champs noir sur les plans [002] représente une structure de miroirs de Bragg. On observe clairement une différence de contraste entre les couches de AlAs et de GaAs. Cela signifie donc que la nature chimique des atomes de la maille a une influence sur l’intensité du flux d’électrons diffractés par l’échantillon.

On construit, par analogie avec le contraste en optique, le facteur de structure. Il fait intervenir :

•         La périodicité du cristal

•         La position des atomes dans la maille

•         La nature chimique des atomes de la maille

•         La constante appelée facteur de diffusion atomique et spécifique à chaque espèce cristalline.

Ici les p atomes de la maille sont tous identiques.

-           (h,k,l) définit les plans cristallins

-          (xp,yp,zp) sont les coordonnées des nœuds où sont situés les atomes de l’espèce chimique j

-          fj est le facteur de diffusion atomique de l’espèce j.

Si le motif est constitué de deux atomes différents, on réécrit le facteur de structure comme

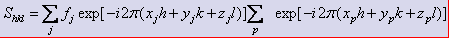
-          la somme sur j est la nouvelle expression du facteur de diffusion atomique, avec (x_j,y_j,z_j) les coordonnées de l’atome j dans le motif. C’est le facteur de forme atomique.

-          (x_p,y_p,z_p) sont les coordonnées du p-ième nœud dans la maille.

Expression du facteur de structure pour une maille de GaAs  [12]

    Le réseau de GaAs est cubique face centrée avec un atome de As en (000) et un atome de Ga en (1/4,1/4,1/4). Ici le facteur fj se décompose en deux facteurs de diffusion atomique, fGa et fGs.

On a F_j= (f_As+ f_Ga .exp ((-iπ/2)(h+k+l)), c’est la contribution du motif

Donc S_hkl= (f_As+ f_Ga .exp ((-iπ/2)(h+k+l))∑ exp(-2iπ(x_j.h+y_j.k+z_j.l)

Avec (x_j,y_j,z_j) = (0,0,0), (0,1/2,1/2),(1/2,0,1/2),(1/2,1/2,0)

On a S_hkl= (f_As+ f_Ga exp ((-iπ/2)(h+k+l)) (1+exp(-iπ(h+k))+exp(-iπ (h+l))+exp(-iπ (l+k))

Si h,k et l n’ont pas la même parité, alors S  est nul. La périodicité du cristal entraîne des extinctions en fonctions de la structure cristalline.

On s’aperçoit également que le facteur de structure pour AlAs va être différent de celui de GaAs car f_Ga ≠f_Al

L'intensité diffractée dans une direction repérée par le triplet d'indices hkl est

I_hkl = |F_hkl|² = F_hklxF_hkl* (imaginaires conjugués)