ACCUEILPLAN DU SITEPOSTER RECAPITULATIFBIBLIOGRAPHIE


II. L’ÉCHANTILLON ET LA THÉORIE DE LA DIFFRACTION


1. Bases de la cristallographie
•

Le critère de l’état cristallin est son caractère ordonné donc périodique à l’échelle atomique.

 •Ce sont Von Laue et Bragg (début du XXème) qui ont apportés la preuve de la nature périodique de l’arrangement cristallin grâce à la découverte de la diffraction des rayons X.

•

•

Le cristal est un réseau constitué de nœuds formant des mailles périodique. Chaque nœud étant décrit par un motif. 

•

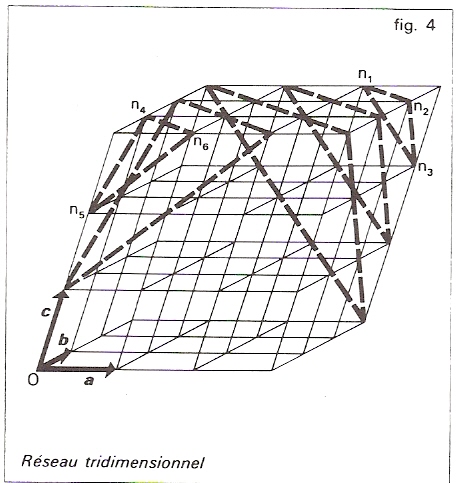
        Un cristal peut être représenté par un réseau à 3 dimensions dont les vecteurs de base a,b,c définissent la maille élémentaire.L’ensemble des nœuds du réseau qui sont aux extrémités des
vecteurs nuvw=ua+vb+wc peuvent être groupés en familles de plans réticulaires équidistants. Les vecteurs a,b,c forment ainsi les vecteurs de base du réseau direct.



•
      
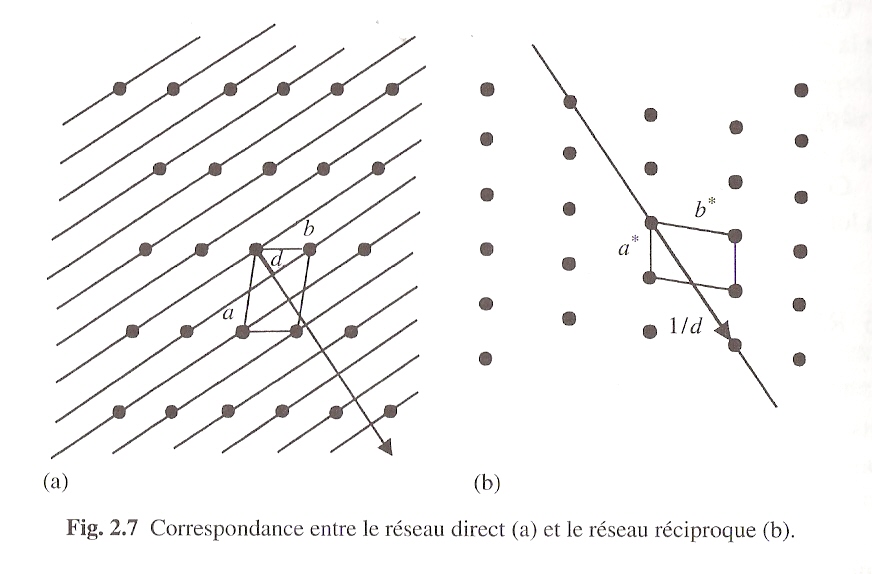
     Le réseau réciproque de ce réseau direct est construit à partir des trois vecteurs de base A,B,C définis par les relations:
                                                           aA=bB=cC=1
                                                 aB=aC=bA=bC=cA=cB=0


        Considérons un vecteur : Nhkl= hA+kB+lC   avec h,k,l  3 entiers quelconques premiers entre eux. Ce vecteurs Nhkl est perpendiculaire à une famille de plans réticulaires du réseau direct. En effet, projetons tous les nœuds du réseau sur le vecteur Nhkl :


Nhkl . nuvw= (hA+kB+lC).(ua+vb+wc )= hu+kv+lw             (1)


        L’ensemble du réseau peut être résolu en une famille de plans réticulaires équidistants et perpendiculaires à Nhkl.
Et d’après (1), dhkl. Nhkl =1.
Les trois entiers h,k,l caractérisent une famille de plans réticulaires, ils sont appelés « indices de Miller ». C'est la périodicité des plans d'une même famille qui crée la diffraction.[5]



 [6]