2.
L’échantillon
a.
Préparation
§
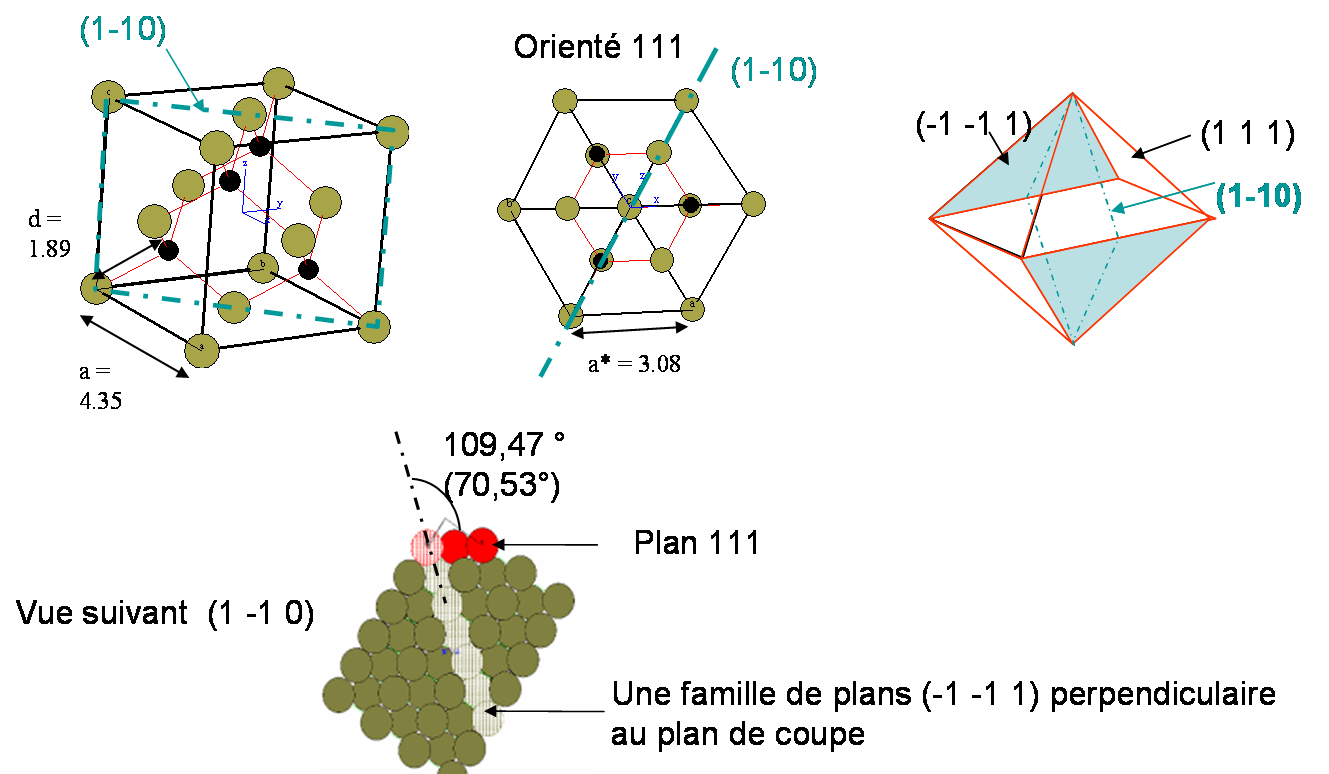
L’échantillon est préparé de manière à être observé selon une direction
voulue.
§La direction [hkl] est
orthogonale au plan (hkl)
Exemple: Observation selon la
direction [1-10] à
coupe dans le plan (1-10)
b.
Diffraction
L’échantillon est placé dans le
microscope. Le faisceau électronique le traverse… et il se produit les phénomènes
physiques suivants:
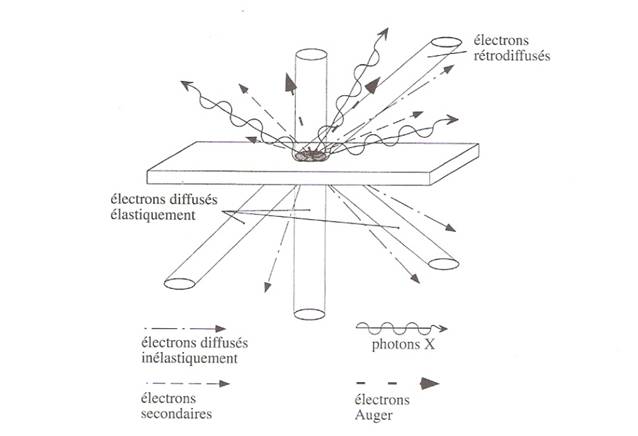
§Chocs élastiques /
chocs inélastiques
•
chocs élastiques: au cours de tels chocs
l’électron (léger) transfère à l’atome une faible quantité d’énergie. Le vecteur
vitesse de l’électron incident change de direction et son énergie ne varie pas de
manière sensible. Les électrons élastiques peuvent interférer de manière constructive dans
certaines directions de l’espace, ce qui est à l’origine des phénomènes de diffraction.
•
•
chocs inélastiques: l’électron incident heurte
un des électrons de l’atome cible. Dans ce cas le transfert d’énergie
entre deux particules de même masse peut être important et modifier temporairement l’état
de l’atome. Il peut y avoir excitation des électrons de valence ou de conduction et
pour des pertes d’énergie plu grandes l’atome peut perdre des électrons de
couches plus profondes.
l’électron qui pénètre dans un
échantillon massif va subir une série de chocs en changent de direction à chaque
interaction et en perdant plus ou moins d’énergie.
• diffusion des électrons par un échantillon cristallin
Les électrons incidents perdent
une partie de leur énergie cinétique par ralentissement lors de la traversée de la
cible. L’émission de photons X correspond à cette énergie perdue.
•Quand l’atome perd des
électrons de couches profondes, celui-ci séjourne très brièvement dans l’état ionisé.
Il se désexcite en cédant de l’énergie sous formes d’émissions caractéristiques
ou d’électrons d’Auger. [7]
§
Diffraction des
électrons élastiques
La
diffraction des rayonnements par les cristaux résulte d’interférences
constructives et
destructives d’ondes.
Loi
de Bragg: on
peut faire l’analogie du phénomène de diffraction par une famille de plans réticulaires (hkl) avec
celui de la réflexion lumineuse par un miroir plan. La différence est que les
faisceaux diffractés par des plans réticulaires ne sont obtenus que pour des angles
d’incidence bien particuliers, vérifiés par la loi de Bragg :
nλ=2dhklsinθn
Avec:
n:
ordre d’interférences.
λ: longueur d’onde du
rayonnement incident.
dhkl: distance entre 2 plans de la
même famille.
θn: angle du rayonnement
incident avec les plans réticulaires.
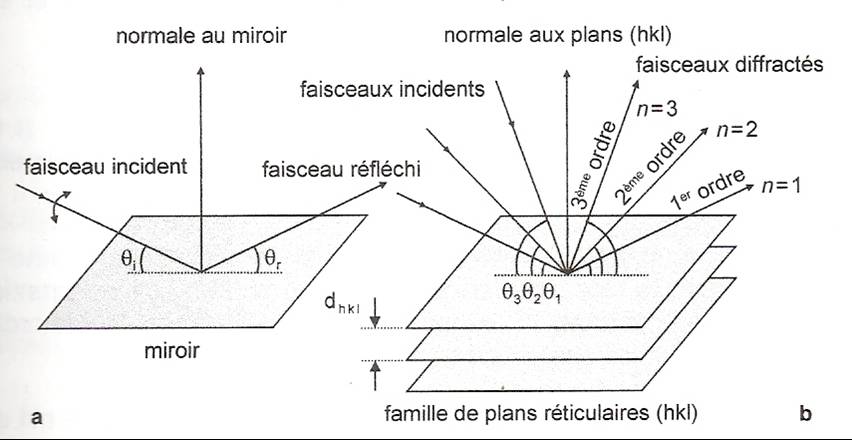
comparaison entre diffraction par une famille de plan et réflexion de faisceaux incidents par un miroir
Remarque: Les faisceaux d’ordre
n>1 sont assimilés à des réflexions de premier ordre sur des plans d’indice (nh nk
nl) et de distance dhkl/n.
En toute rigueur les plans (nh
nk nl ) ne sont pas des plans réticulaires. Comme ils ont des indices non premiers entre
eux, ils ne contiennent pas tous des nœuds du réseau direct. Pour cette raison ils
sont parfois appels plans réflecteurs.
L’angle entre un faisceau
diffracté et son faisceau transmis correspondant vaut 2θbn: il s’agit de l’angle de diffraction.
La longueur d’onde λ étant très faible, les angles
de Bragg sont très petits et la loi de Bragg peut s’écrire nλ=2dhklθbn
Du coup les plans susceptibles
de diffracter les électrons sont ceux qui sont parallèles ou presque parallèles au
faisceau incident.
 cône de faisceaux incidents en conditions de Bragg par rapport à une famille de plans réticulaires
cône de faisceaux incidents en conditions de Bragg par rapport à une famille de plans réticulaires
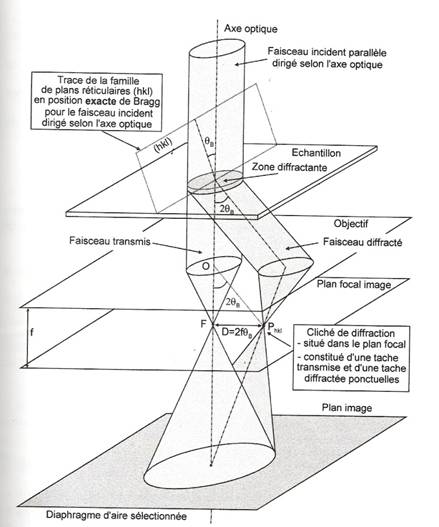
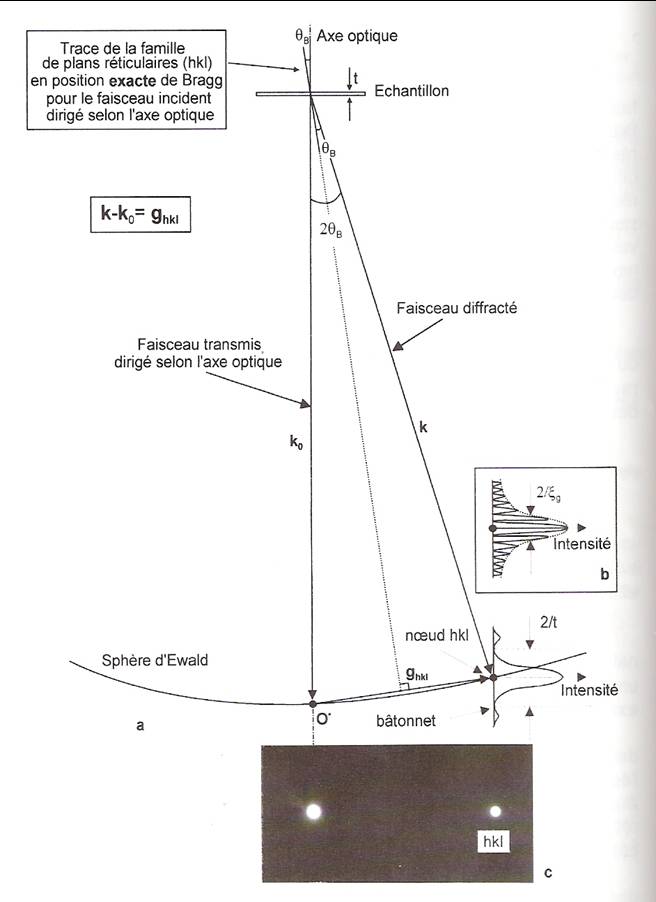
Diffraction par une famille de plans (hkl) en position exacte de Bragg
Exemple
: Principaux plans qui
diffractent dans la direction [1-10]
Les plans
111, 220, 002 sont parallèles ou quasi parallèles au faisceau électronique
incident selon l’axe de zone [1-10]
§
Interprétation
géométrique de la loi de Bragg: la sphère d’Ewald
C’est
une construction simple qui permet de représenter le phénomène de
diffraction. Elle
est constituée :
•D’une sphère de rayon R=1/λ
•Du rayon incident dirigé selon
AO
•De l’échantillon placé au
centre O de la sphère.
•Du réseau réciproque dont
l’origine O* est située à l’extrémité de AO*.
Un
faisceau diffracté (hkl) est produit si un nœud (hkl)
du
réseau réciproque est exactement situé sur la
sphère
d’Ewald. Dans ce cas la loi de Bragg est vérifiée
pour
la famille de plans réticulaires (hkl) correspondante.
En
effet on a d’après le schéma : sinθb=O*P/AO*=ghkl/(2*(1/ λ))= λ/dhkl
On
retrouve donc λ=2dhklsinθb
Représentation de la sphère d'Ewald
Remarques :
•
remarque 1: La très faible longueur d’onde λ associé à un faisceau d’électrons accélérés rend le rayon R très grand par rapport à la norme ghkl des vecteurs du réseau réciproque.
•La très faible épaisseur des lames minces entraîne un relâchement des conditions exactes de Bragg. Les nœuds du réseau réciproque ne sont plus ponctuels mais deviennent allongés. L’intensité diffractée selon un bâtonnet n’est pas constante.
La sphère d’Ewald a donc plutôt l’aspect ci-dessous : Les clichés de diffraction ne représentent que le faisceau transmis et le faisceau diffracté par une famille de plan (hkl).
Intersection de la sphère d'Ewald avec le réseau réciproque.
Les points de ce réseau ont une intensité ayant l'allure de gaussiennes
•
remarque 2: Dans le cas de plan (hkl) en position proche de la position exacte de Bragg, l’angle incident n’est pas tout à fait égal à l’angle de Bragg.
On obtient la figure et le cliché de diffraction ci-contre:
La construction d’Ewald indique que:
•
L’angle de diffraction est très peu affecté ce qui signifie que la géométrie
du cliché de diffraction n’est pratiquement pas modifiée par une faible
désorientation du cristal.
•
L’intensité du faisceau diffracté est très fortement affectée, car cette intensité
dépend de l’endroit du bâtonnet qui est coupé par la sphère d’Ewald.
L’intensité du cliché de diffraction est donc très fortement modifiée par une
faible désorientation du cristal. [8]
Intersection
de la sphère d'Ewald avec le
réseau réciproque en
conditions inexactes de Bragg
§
Cliché de diffraction en condition multi-ondes
•Jusqu’ici nous n’avons considéré qu’une seule famille de plans en condition exacte ou approchée de Bragg.
•Généralement plusieurs familles de plans peuvent vérifier les conditions de Bragg (voir positionnement en axe de zone). Le raisonnement plus haut s’applique alors à toutes les familles concernées.
•Pour la construction d’Ewald cela signifie que plusieurs bâtonnets coupent simultanément la sphère d’Ewald.
exemple: Diagramme de diffraction SiC et Si dans l’axe de zone [1-10]