Bandes interdites photoniques

Loi de Bragg

La loi de Bragg établit un lien entre la distance séparant les atomes d'un cristal et les angles sous lesquels sont principalement diffractés des ondes électromagnétiques envoyés sur le cristal.
                                                          
On a la relation ci-dessous :

2d sinθ = m λ

• d = distance interréticulaire
• θ  l’angle de Bragg(c’est le demi-angle de déviation)
• m = ordre de diffraction (nombre entier)
• λ = longueur d'onde

 Explication géométrique de la Loi de Bragg

On considère donc un faisceau de photon envoyé sur un cristal avec un angle Ө. On s’attend a ce que les ondes soit en partie transmises, et en partie diffractées.

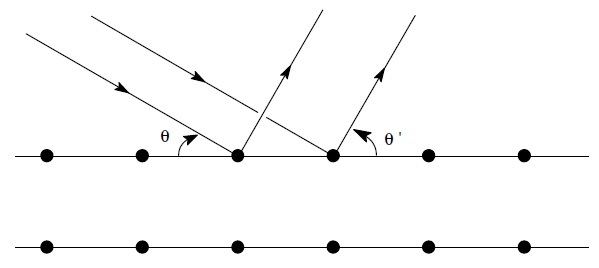
Considérons tout d’abord deux rayons incidents parallèles diffusés par deux particules sur le même plan (figure 1) :

On peux en tirer géométriquement la différence de marche entre les deux rayons :

d = d(cosθ - cosθ') 

Les interférences sont constructives uniquement si la différence de marche introduit un déphasage multiple de 2π, c'est-à-dire si d = mλ.

Cette condition implique que m = 0 et θ = θ'.

On peux donc en conclure que les interférences constructives ont lieu dans une direction qui correspond à la réflexion du signal incident sur le plan réticulaire.

On considère maintenant la réflexion de deux rayons incidents sur deux plans réticulaires parallèles distants de d. (figure 2)

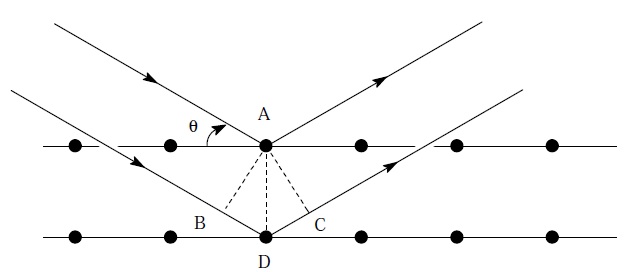
Notre construction implique que les angles BAD et DAC sont égaux et de valeur θ.

On peux donc aisément en tirer la différence de marche BD + DC = d = 2d sin θ.

Comme dans le cas précédent, nous avons des interférences constructives si d = mλ.

On retrouve donc bien la loi de Bragg :  2d sinθ = m λ

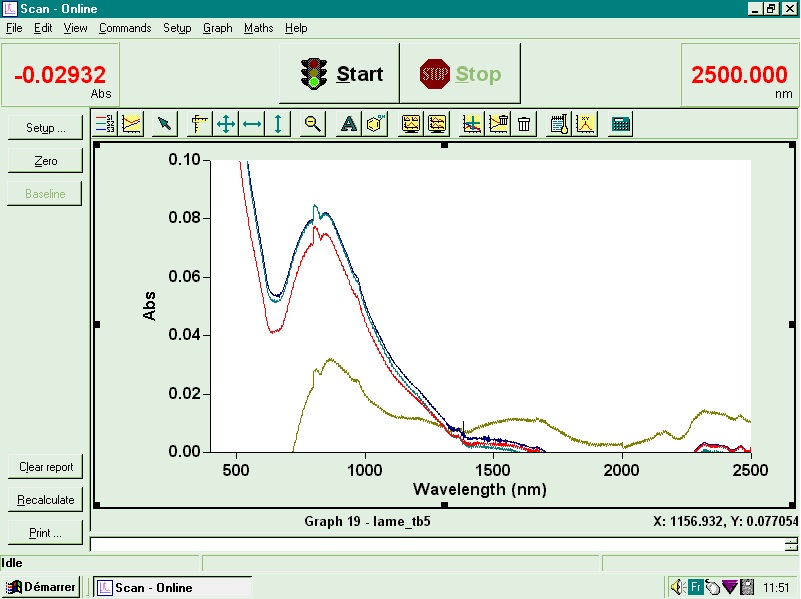
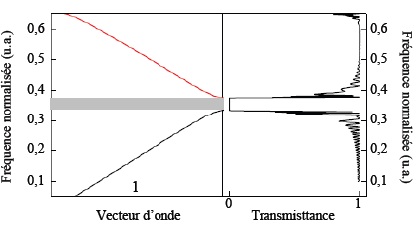
Diagramme de bandes du cristal à gauche, et courbe de la réflexion à droite en fonction de la fréquence des ondes:

Courbes représentant l’absorption d’un faisceau dans une gamme de longueur d’onde allant de 0 à 2500nm.