1. Modélisation
Pour notre projet, nous avons sélectionné les éléments les plus pertinents en ce qui concerne la transmission et émission du potentiel d'action, et nous les avons simplifiés, de manière à concevoir un modèle de neurone à la fois simple et réaliste.
Ainsi nous n'avons pas gardé tout ce qui concerne la perméabilité de la membrane aux ions. Le potentiel d'action est affecté de la valeur 0 ou 1, si il est déclenché ou pas, gardant de ce fait le caractère tout ou rien de celui-ci.
Les synapses se font entre l'axone et une dendrite.
La dendrite est composée de plusieurs compartiments. Chaque compartiment, qui représente une portion de la dendrite, est affecté d'un coefficient d'atténuation qui tient compte de l'effet des courants de fuite, et d'un coefficient de propagation.
Nous divisons l'arborescence dendritique en compartiments qui rendent compte de la propagation d'un potentiel en particulier graduel et de la longueur de la dendrite. Cela nous permet de modéliser la dendrite en une seule dimension afin de réduire le nombre de calculs. A chaque pas de temps, une partie du potentiel dans la dendrite est dissipée par les courants de fuite, une autre est transmise au compartiment suivant ( ou au soma ), la dernière reste dans le compartiment et sera ajoutée aux potentiels qui arrivent à ce pas de temps par les synapses et le compartiment précédent.
La synapse est caractérisée par une valeur, le poids synaptique.
Le poids synaptique, un élément important de notre modélisation, est une valeur positive ou négative plus ou moins importante qui rend compte de l'importance de la synapse et si elle est inhibitrice ( négative ) ou excitatrice ( positive ). Nous pouvons choisir sur quels compartiments de la dendrite du neurone récepteur nous connectons la synapse. Il y a une valeur de poids différente pour chaque synapse.
Le soma est caractérisé par son seuil de dépolarisation, son courant de fuite, et son potentiel membranaire, fixé ici à zéro. Il ne peut déclencher un potentiel d'action que si il n'en a pas déclenché au temps précèdent : c'est la modélisation de la période réfractaire.
Le délai synaptique représente notre base de temps de calcul. Il n'intervient pas directement dans les formules. La valeur de potentiel au temps d'après se calcule à l'aide de la valeur du potentiel au temps d'avant.
Maintenant, considérons un réseau de i neurones avec une dendrite modélisée en k compartiments. Les calculs sont discrétisés. 7 Mathématiquement:
C(i ,k )(t+ 1)=C(i , k)(t)∗(1−PD(i , k )−CF(i ,k ))+ PD(i ,k−1)∗C(i , k−1)(t)+ a j(t−DS( j , i , k))∗PS( j ,i ,k )
-Nous permet de calculer le potentiel dans le compartiment k de la dendrite du neurone i au temps t+1. Où, C(t) est le potentiel dans le compartiment au temps t; PD le coefficient de propagation; CF le coefficient d'atténuation; aj le potentiel post-synaptique; DS le délai synaptique et PS le poids synaptique.
-Nous utilisons la formule suivante pour calculer ce qui se trouve dans le soma au temps t+1
si ai(t)=0alors si (t+ 1)=si(t )(1−CF(i ,0))+ PD(i ,1)∗C(i ,1)(t)
sinon si(t+ 1)=si(t)(1−CF(i ,0))+ PD(i ,1)∗C(i ,1)( t)−SDi
avec SD le seuil de dépolarisation du neurone i.
-Nous déterminons enfin, si un potentiel d'action est déclenché avec: ai(t )=1 si si(t)≥SDi et si ai (t)=0
ai(t )=0 sinon
2. Premières simulations avec Excel
Dans un premier temps, nous avons cherché quels étaient les réseaux pertinents à considérer, c'est-à-dire ceux qui semblent logiques d'une part mais surtout biologiques d'autre part et qui permettent d’effectuer des opérations d’intégration intéressante du point de vue computationnel. Nous en avons identifiés 4:
- un réseau où plusieurs neurones se suivent, connectés en série. C'est le réseau le moins complexe. Pour des entrées données on aura ou pas une réponse, tout dépend de la fréquence de ces entrées, du poids synaptique, du seuil de dépolarisation. Si le seuil de dépolarisation est élevé alors les sorties sont de plus en plus rares. De même si le poids synaptique est faible à un seuil donné.
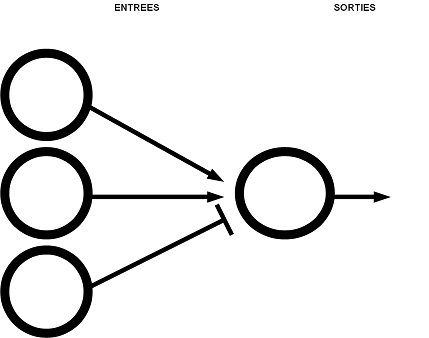
- un réseau de neurones où un neurone reçoit la sortie de trois neurones différents. C'est un
réseau semblable à celui en série mais nous pouvons mettre en évidence l'influence d'une entrée en
particulier c'est-à-dire inhibitrice ou excitatrice, ou encore la force du poids synaptique d'une entrée.
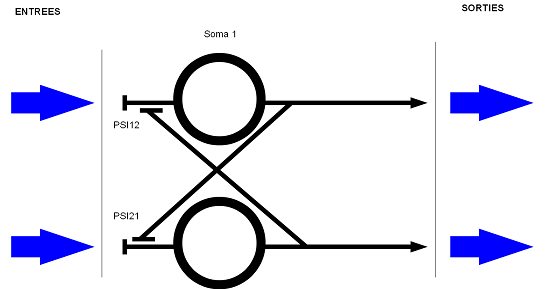
- un réseau de neurones en parallèle avec une interaction inhibitrice entre les deux neurones
( pour deux entrées différentes il y aura deux sorties différentes ). Un des deux neurones prend le
pas sur l'autre ( il y a un chemin qui est privilégié ).
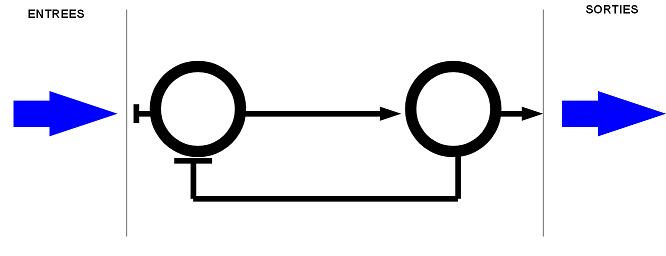
-
un réseau de neurones avec une boucle de rétroaction inhibitrice. Ce réseau permet de
réguler la sortie lorsque qu'il y a de nombreuses entrées.
Dans un deuxième temps, les simulations sur le logiciel Excel de ces réseaux permettent de bien ressentir l'influence des paramètres ( le poids synaptique, la valeur du seuil... ). Nous avons adapté les formules déduites de notre modélisation au logiciel Excel et au réseau programmé. Puis nous avons donné des entrées arbitraires pour chaque pas de temps et nous avons calculé les valeurs des potentiels dans chaque compartiment et chaque soma des neurones du réseau simulé. Puis nous avons tracé des graphes représentants l'évolution des potentiels en fonctions de certains paramètres du réseau.
Pour le réseau « 2 », en fixant les entrées des trois neurones aléatoirement, et en fixant les paramètres comme la valeur du seuil et les poids synaptiques, on obtient le graphe suivant:
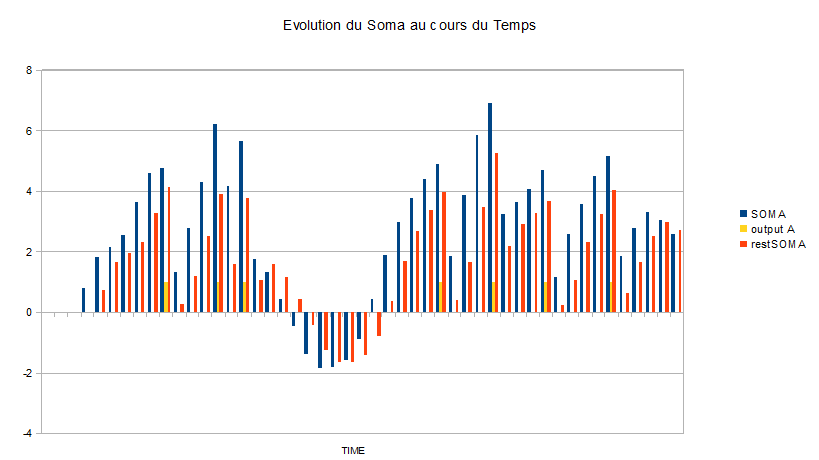
Ce graphe donne l'évolution du potentiel dans le soma du neurone qui reçoit trois entrées simultanées : une inhibitrice et deux excitatrices. Il y a le potentiel total dans le soma ( bleu ), la valeur du potentiel qui est conservée dans le soma après les pertes ( rouge ) et le potentiel d'action déclenché ( jaune ). Une fois que le seuil de dépolarisation est atteint ( ici 4 ) au temps t, un potentiel d'action est déclenché au temps suivant : par exemple au temps 8 le seuil est dépassé et il y a un potentiel d'action au temps 9. D'autre part, nous notons que l'entrée inhibitrice permet de réguler l'émission de potentiels d'action et même de diminuer le potentiel du soma en dessous de son potentiel de repos ( ici 0 ). Nous pouvons aussi voir que si le seuil de dépolarisation était deux fois plus faible, par exemple, la fréquence des potentiels d'action serait beaucoup plus importante de l'ordre d'une vingtaine de potentiels au lieu de sept potentiels.
Pour le réseau « 3 » nous avons tracé le nombre de potentiels d'action en sortie (output) pour différentes valeurs des poids synaptiques entres les deux neurones.
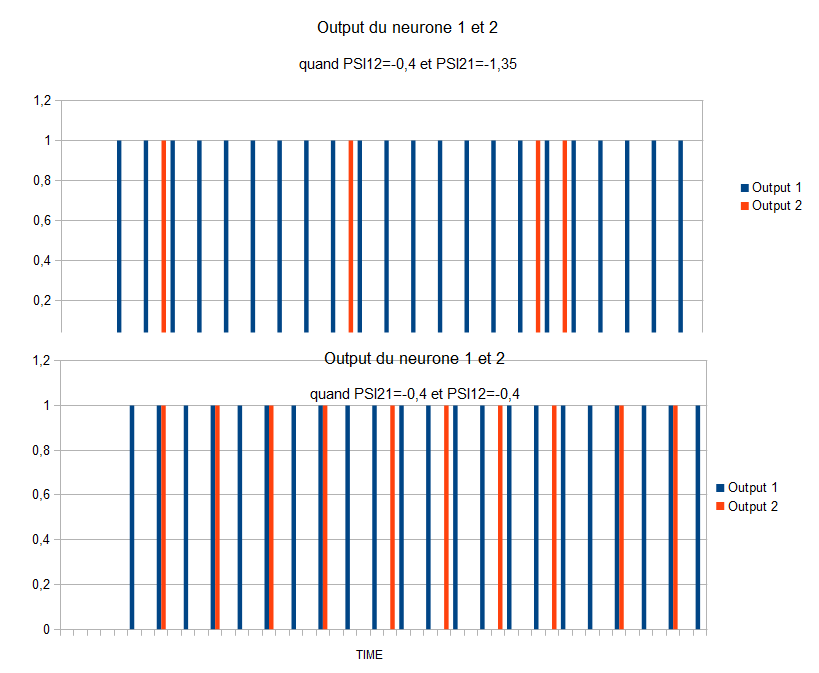
Ce graphe met en évidence l’influence du poids synaptique sur le nombre de potentiels d'action en sortie. Si un des poids synaptiques qui intervient dans l’interaction inhibitrice entre les deux neurones est très fort, alors l'action du deuxième neurone et complètement entravée. En effet, le poids synaptique du premier neurone amplifie l'effet inhibiteur du potentiel d'action qui diminue d'autant plus la dépolarisation du deuxième neurone, ce qui a pour conséquence d'empêcher cedernier d'atteindre son seuil de dépolarisation et à son tour ne peut pas déclencher de nouveaux potentiels d'action et finalement ne peut pas agir sur le premier neurone. De la même manière, si une entrée est plus forte, elle inhibe la sortie de l'autre neurone. Nous retenons que ce réseau permet de privilégier l'une ou l'autre des deux sorties.
3. Codage des réseaux en Java
Nous nous sommes familiarisés avec le langage de programmation JAVA sur le logiciel Netbeans IDE. Ensuite nous avons modifié le programme initial afin de créer les structures de base que nous avons identifiées. Puis nous les avons mises en relation pour créer des réseaux plus grands. Nous avons commencé à créer des réseaux qui correspondent aux comportements que nous voudrions donner à notre robot. Le robot devrait notamment pouvoir explorer, détecter la nourriture, réagir au danger. Normalement nous aurions dû écrire le programme qui permet de connecter ces structures avec les capteurs et les servomoteurs du robot, mais par faute de temps cela n'a pas été terminé. Puis c'est ce programme là que nous aurions implémenté dans le microprocesseur du robot.
Le programme qui code les réseaux de neurones ressemble a celui-ci:
public class NeuroNetwork {
public List
public int [] output_t;
public int [] output_tplus;
public int [] input_t;
public int [] input_tplus;
Et pour les réseaux que nous modélisons, par exemple pour le réseau 3
for(int t=0;t<=26;t+=1)
{
System.out.println("\nt = "+t);
nwkMultipleParallelTwo.input_t[0] = 1;
nwkMultipleParallelTwo.input_t[1] = 1;
nwkMultipleParallelTwo.input_t[2] = 1;
nwkMultipleParallelOne.input_t[0] = 1;
nwkMultipleParallelOne.input_t[1] = 1;
nwkMultipleParallelOne.input_t[2] = 1;
nwkMultipleParallelOne.input_t[3] = nwkMultipleParallelTwo.output_t[0];
System.out.println("NETWK OUTPUT 1 = "+nwkMultipleParallelTwo.output_t[0]);
nwkMultipleParallelOne.configurationToActivate_MultipleParallel(
nwkMultipleParallelOne.input_t /*nwkMultipleParallelTwo.input_t*/, t);
nwkMultipleParallelTwo.input_t[3] = nwkMultipleParallelOne.output_t[0];
System.out.println("NETWK OUTPUT 1 = "+nwkMultipleParallelOne.output_t[0]);
nwkMultipleParallelTwo.configurationToActivate_MultipleParallel(
nwkMultipleParallelTwo.input_t /*nwkMultipleParallelTwo.input_t*/, t);
En plus du code des réseaux nous avons un code de "neurone" qui définit le neurone et ses propriétés, comme le seuil de dépolarisation, le nombre de neurone, les courants de fuite, le nombre de compartiments ou encore le poids synaptique.
public double compartment_t;
public double compartment_tplus;
public int outputAxon;
public double threshold;
public double decayPropa;
public double leakCurrentCompartment;
public double leakCurrentSoma;
public double singleWeight;
public double s_t;
public double s_tplus;
public int outputAxon_t;
public int outputAxon_tplus;
public int neuronNb;
if(s_tplus>threshold){
outputAxon_tplus=1;
}
else{
outputAxon_tplus=0;
public void setInputCompartment(int input){
compartment_tplus=((double)input)*singleWeight
+compartment_t*(1-leakCurrentCompartment-decayPropa);
}