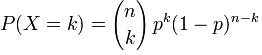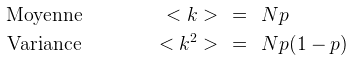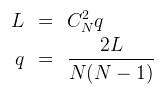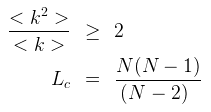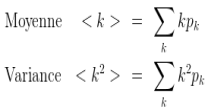Les réseaux complexes :
Les graphes aléatoires ont été introduits par Erdös et Rényi en 1959 pour prouver certains résultats combinatoires sur les graphes, tel qu'une borne inférieure sur les nombres de Ramsey par exemple. De manière générale, un graphe permet de représenter la structure, les connexions dun ensemble complexe en exprimant les relations entre ses éléments : réseau de communication, réseaux routiers, interaction de diverses espèces animales, circuits électriques...
Les graphes aléatoires peuvent être également utilisés pour évaluer la complexité en moyenne d'algorithmes ou encore pour modéliser devrais réseaux de la vie de tous les jours, comme les réseaux sociaux et internet. Plusieurs modèles de graphes aléatoires existent. Le choix du modèle doit être fait avec soin car les propriétés des graphes peuvent être très différentes selon le modèle choisi. Les graphes constituent ainsi un outil mathématique qui permet de modéliser une grande variété de problèmes en se ramenant à létude de nuds et de liens. La théorie des graphes sest alors développée dans diverses disciplines telles que la physique, la chimie, la biologie, les sciences sociales...
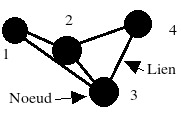
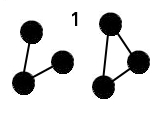
Pour résumer un réseau complexe est tout simplement une modélisation d'un système sous la forme de noeuds et de liens. Chacun de ces noeuds et liens peuvent avoir un poids différent dans ce système. Par exemple sur la droite une modélisation sous forme de réseau complexe d'une discussion entre 4 individus. Le premier ne communique qu'avec ses deux plus proches voisins sur l'exemple.
Prenons la figure suivante :
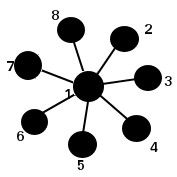 L'importance d'un noeud dans un réseau :
L'importance d'un noeud dans un réseau :
En l'observant, on comprend que l'importance du noeud 1 est beaucoup plus grande devant celle des autres. Si celui-ci est enlevé une information ne pourra plus circuler entre tout les autres noeuds.
Maintenant si l'on imagine que ce système reprèsente un réseau éléctrique on comprend que celui-ci sera très fragile et qu'il est vital de l'optimiser.
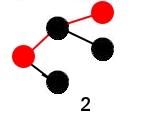
Cependant si l'on transforme notre figure en celle-ci :
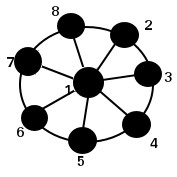 Le noeud 1 n'a plus autant d'importance qu'avant mais il permet de réduire la profondeur des noeuds se situant sur son périmetre de 3 à 2. Il permettra juste une transmission plus rapide de l'information.
Le noeud 1 n'a plus autant d'importance qu'avant mais il permet de réduire la profondeur des noeuds se situant sur son périmetre de 3 à 2. Il permettra juste une transmission plus rapide de l'information.
Nous allons d'abord introduire les principales caractéristiques de notre réseaux et introduire quelques définitions :
Rappels mathématiques :
Petit rappel sur la loi binomiale qui servira dans la partie suivante :
Soit une expèrience aléatoire et renouvellé n fois de manière indépendante ayant deux issus possible. On a une chance de tomber k fois sur l'événement ayant une probabilité p égale à :
Caracteristiques générales des réseaux :
-
Nous travaillerons sur des réseaux n'ayant pas de "preferencial attachment", c'est à dire que la probabilité de connexion ne dépent pas d'un noeud en particulier.
Pour un réseau contenant N noeuds et L liens avec un probabilité de connexion q on aura par définition :
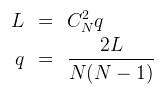
En effet, il ya équiprobabilité entre les noeuds. Donc on peut exprimer le nombre de liens total dans le système comme le produit des combinaisons possibles entre deux noeuds et la probabilité de connexion pour un noeud.
- De plus pour qu'un système soit percolé on doit avoir :
Pour chaque réseau on peut chercher à établir un seuil de percolation. C'est en quelque sorte un critére sur le degré qui permet, si il est vérifié par le système, de dire que ce dernier est percolé.
Il existe plusieurs méthodes pour déterminer cette valeur. Entre autre considérer les clusters ou bien s'intéresser au degré moyen et à la variance.
Nous n'avons pas calculé la taille des clusters. Mais nous avons interprété le problème de la façon suivante.
Considérons un réseau composé d'une infinité de noeuds reliés de manière à former une ligne.
Lorsque nous calculons la moyenne de degré nous obtenons 2 et la variance associée donne 4. Le rapport variance sur moyenne donne 2. Le système étant percolé par construction, on peut être sur que tout système dont ce rapport est suppérieur ou égal à deux peut être considéré comme percolé.
Une fois ce critére obtenu on peut obtenir des paramétres dits critiques comme le nombre critique de lien que nous évoquons.
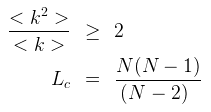
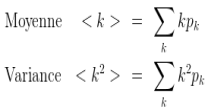
avec Lc le nombre de liens critique de notre système.

 L'importance d'un noeud dans un réseau :
En l'observant, on comprend que l'importance du noeud 1 est beaucoup plus grande devant celle des autres. Si celui-ci est enlevé une information ne pourra plus circuler entre tout les autres noeuds.
Maintenant si l'on imagine que ce système reprèsente un réseau éléctrique on comprend que celui-ci sera très fragile et qu'il est vital de l'optimiser.
L'importance d'un noeud dans un réseau :
En l'observant, on comprend que l'importance du noeud 1 est beaucoup plus grande devant celle des autres. Si celui-ci est enlevé une information ne pourra plus circuler entre tout les autres noeuds.
Maintenant si l'on imagine que ce système reprèsente un réseau éléctrique on comprend que celui-ci sera très fragile et qu'il est vital de l'optimiser.
 Le noeud 1 n'a plus autant d'importance qu'avant mais il permet de réduire la profondeur des noeuds se situant sur son périmetre de 3 à 2. Il permettra juste une transmission plus rapide de l'information.
Le noeud 1 n'a plus autant d'importance qu'avant mais il permet de réduire la profondeur des noeuds se situant sur son périmetre de 3 à 2. Il permettra juste une transmission plus rapide de l'information.