
Système actif de stabilisation d’un interféromètre de Michelson en vue d’applications en communication quantique.
Projet tuteuré en Laboratoire
Laboratoire de Physique de la Matière Condensée
Université de Nice - 2015/2016
Encadrants : Virginia D'Auria et Florian Kaiser
Introduction
De nombreux systèmes utilisés de nos jours se doivent d'être stables. Pour cela nous utilions des correcteurs qui vont les soumettre à des consignes données.
Nous allons construire l'un de ces systèmes, l'adapter à un interféromètre, et l'appliquer à une expérience d'optique quantique.


Intérieur du PID

PID de l'extérieur
Interféromètre de Michelson
L'interféromètre de Michelson est un dispositif permettant de séparer un rayon lumineux en deux et de faire interférer les deux faisceaux ainsi obtenus entre eux.
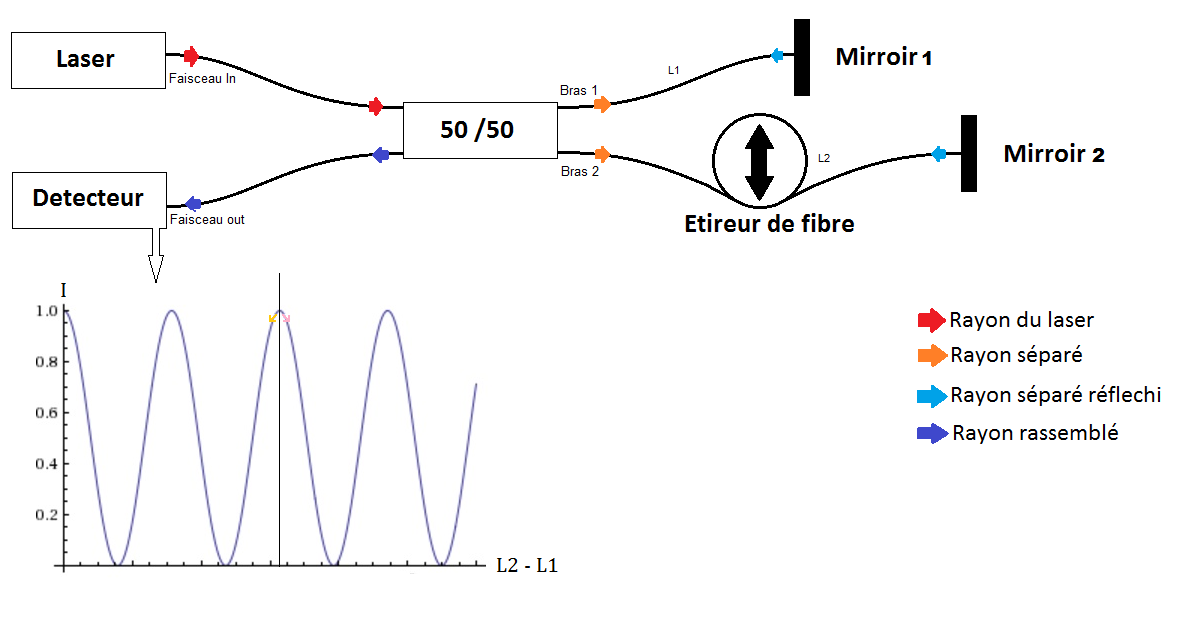
Schéma d'un Michelson en fibres optiques ainsi que son signal de sortie.
Notre système est très sensible aux différences de temperatures : Pour une différence de 1 K nous avons un décallage de 2/3 de frange d'interférence.
Nous voulons que le système soit stable. Nous allons donc utiliser un correcteur pour éviter les perturbations.
PID
Pour contrôler notre interféromètre nous alons utiliser un controlleur PID (Proportionnel Intégrateur Dérivateur) relié au cristal piézoélectrique, qui changera la longueur du chemin long afin de faire correspondre le signal de sortie à un signal consigne.
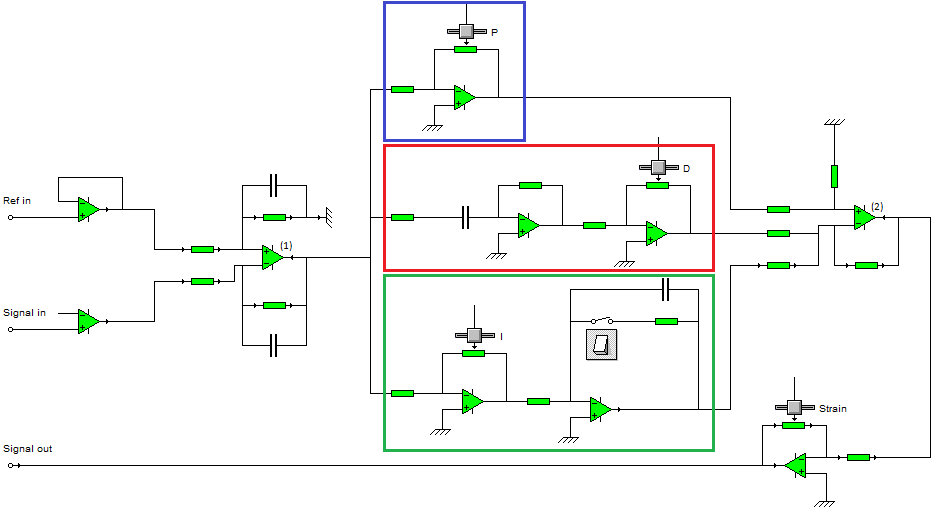
Schéma électrique du PID contruit et utilisé.

Chacun des 3 paramètres peuvent être réglés afin de rapprocher le signal corrigé de la consigne.
Les trois choses à réduire sont :
-Le temps de montée
-Le dépassement
-L'erreur statique
Nous allons régler les paramètres du PID chacun leur tour dans l'ordre suivant (P -> D -> I)
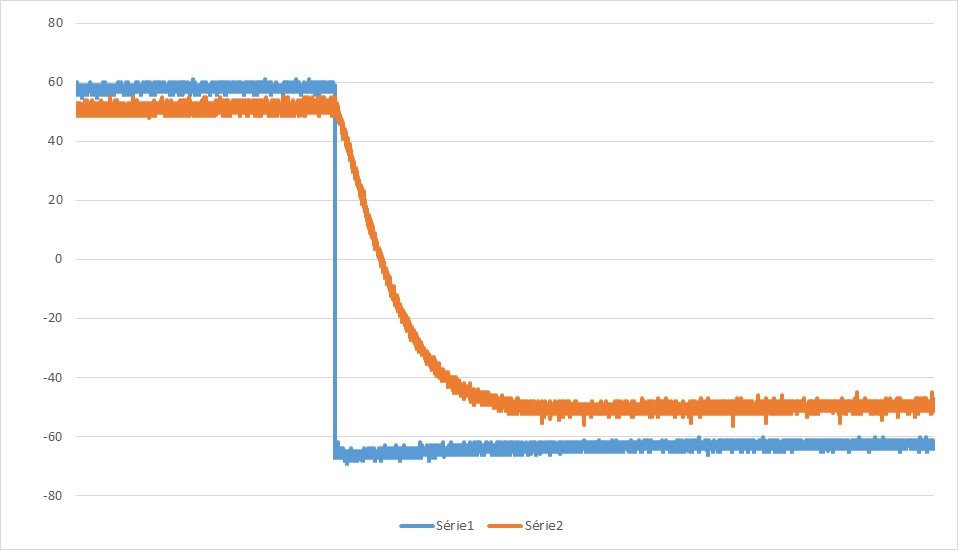
1. P=3,74Ω ; D=0Ω ; I=0Ω
2. P=9,85kΩ ; D=0Ω ; I=0Ω
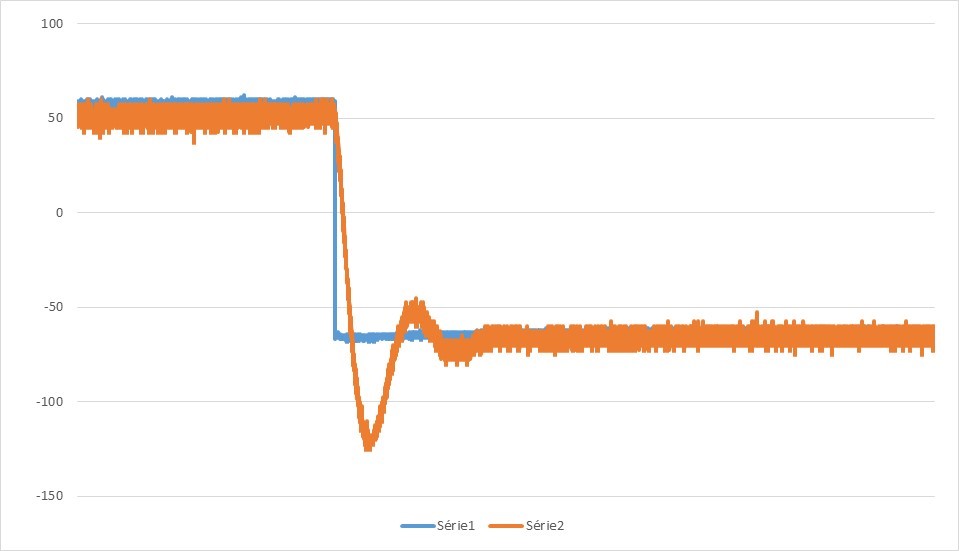
3. P=48kΩ ; D=0Ω ; I=0Ω
Le meilleur paramètre sur P a été trouvé (figure 2). Nous allons maintenant faire décroître la courbe plus rapidement et corriger le petit dépassement avec le dérivateur.

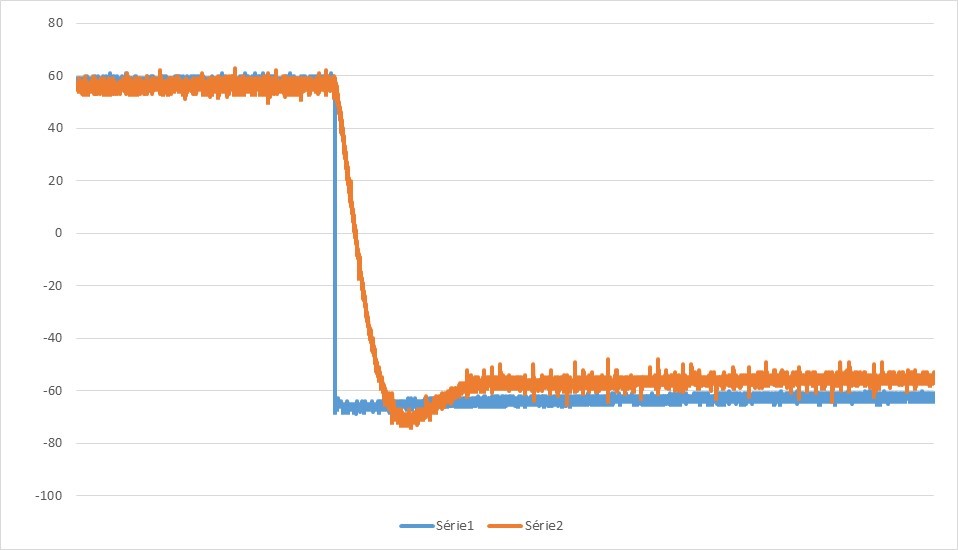
4. P=9,85kΩ ; D=0Ω ; I=0Ω
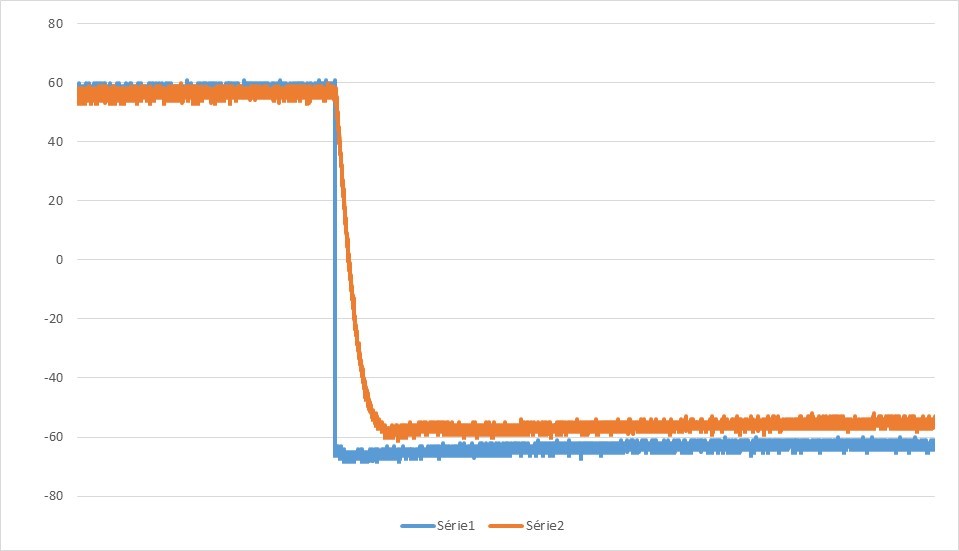
5. P=9,85kΩ ; D=14,4kΩ ; I=0Ω
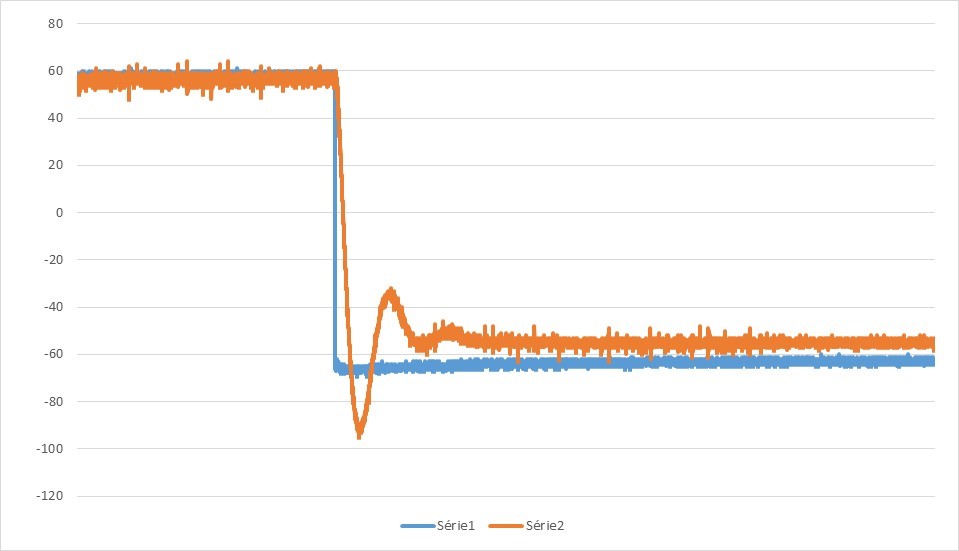
6. P=9,85kΩ ; D=67kΩ ; I=0Ω
La courbe décroit bien plus rapidement avec l'ajout du dérivateur (la figure 5 étant la meilleure), mais il reste encore un écart entre la consigne et le signal de sortie. L'intégrateur va régler ce problème.

7. P=9,85kΩ ; D=14,4kΩ ; I=0Ω
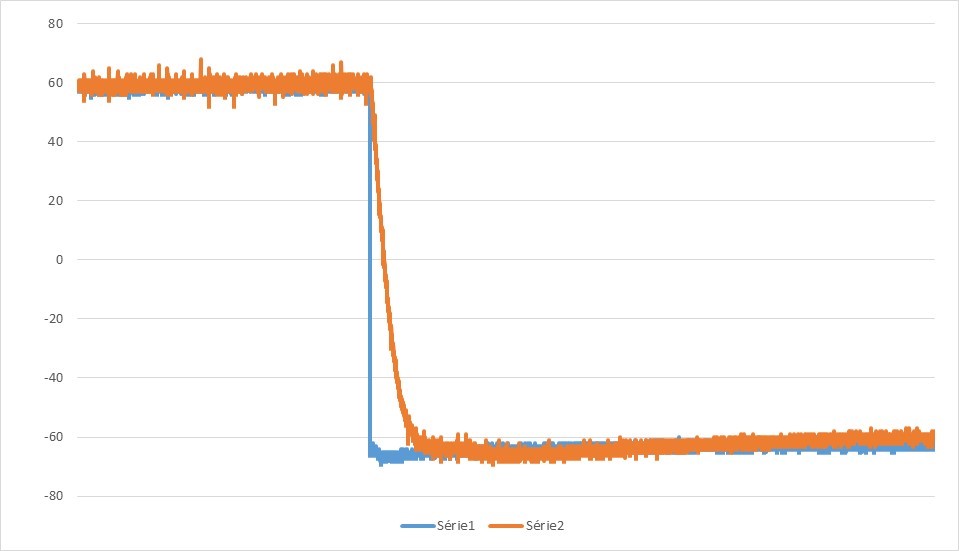
8. P=9,85kΩ ; D=14,4kΩ ; I=5,8kΩ
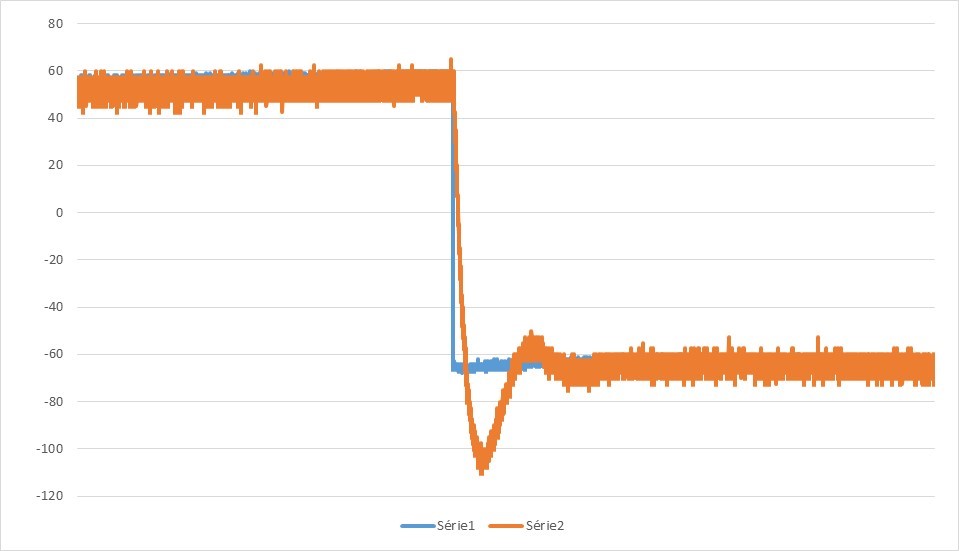
9. P=9,85kkΩ ; D=14,4kΩ ; I=39kΩ
Notre PID est maintenant correctement réglé et répond rapidement(figure 8). Notre système est stable.
Optique Quantique
Nous voulons tout d'abord créer deux photons qui soient intriqués. Pour cela nous alons nous munir d'un laser continu de de longueur d'onde de 780 nm et d'un cristal PPLN (Periodicaly Poled Lithium Niobate) qui a un effet de convertisseur bas et permet d'obtenir à partir d'un photon que l'on nommera Pompe, deux photons, Signal et Idler.
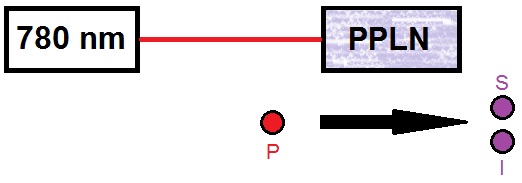
Nous n'avons aucune information sur le moment de la création mais nous savons qu'ils obéissent à la conservation de l'énergie :
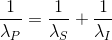
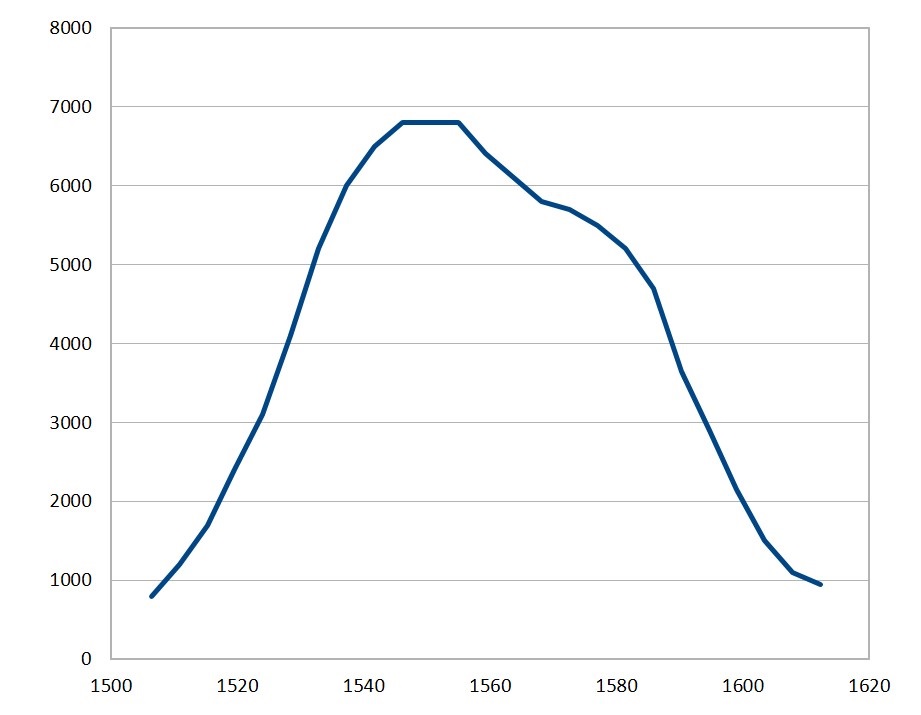
Pour un laser chauffé à 122°C, nous observons le spectre de photons à la sortie du PPLN suivant :
L'expérience suivante est un teste de coïncidences sur les photons que nous venons de créer. On branche à la sortie du PPLN un Beamsplitter, qui est lui-même relié à deux interféromètres identiques à ceux présentée dans les parties précedentes (ici représentés par des Mach-Zehnder pour plus de lisibilité).
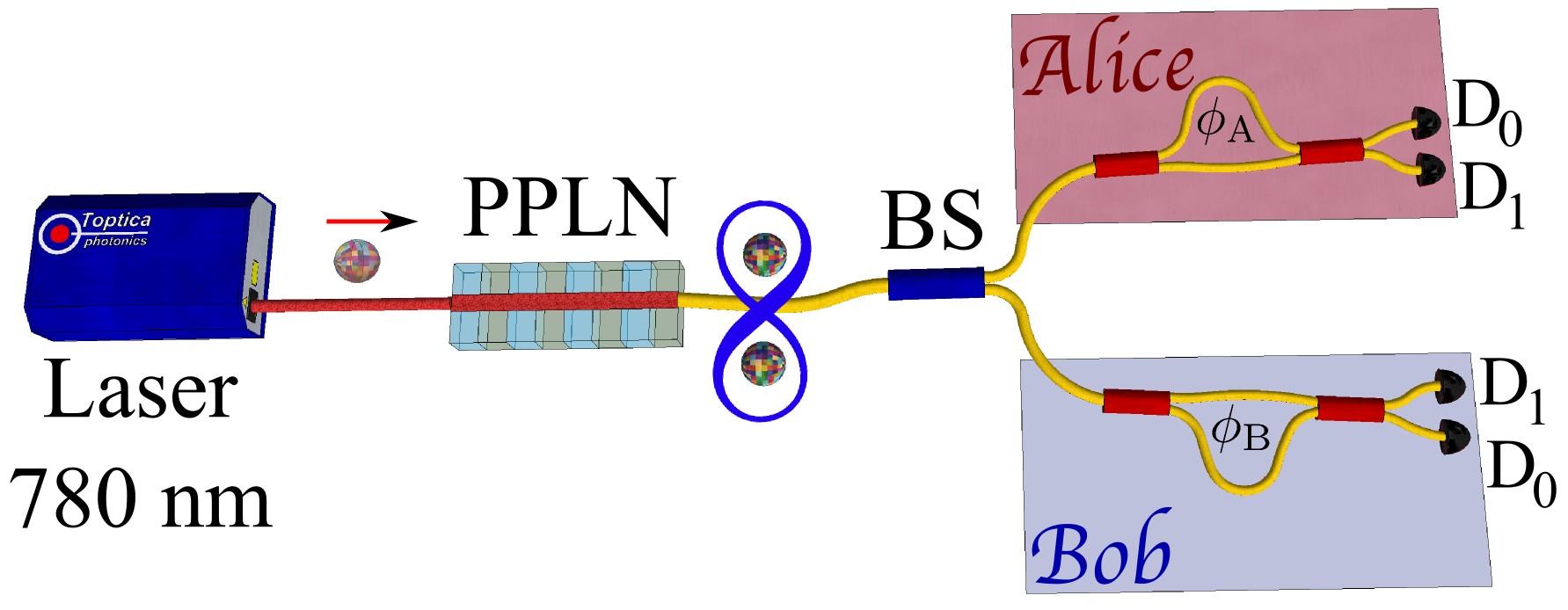
Schéma du dispositif utilisé pour l'expérience.
En sortie les photons ont deux possibilité par interféromètres 0 et 1.
La corrélation entre les deux photons est donnée par :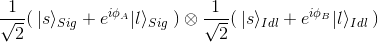
Si les deux interféromètres sont les mêmes, on a :
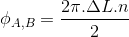
Nous ne tenons compte que des photons arrivant en même temps (ce qui exclut donc les cas où l'un a pris le chemin court et l'autre le long). Ne connaissant pas leur temps d'emission, nous ne pouvons pas savoir si les deux photons ont choisi les chemins courts ou longs.
Après quelques calculs plutôt longs, nous arrivons à des résultats plutôt intéressants.
Les probabilités d'amplitudes sont :
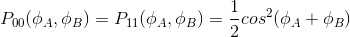
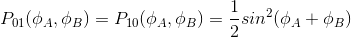
Ces résultats indiquent que pour des interféromètres identiques, les corrélations sont données par les phases.
Pour φA=φB=0 , les correlations sont parfaites :
Si Alice obtient un 0, alors Bob a aussi un 0.
Nous voyons donc là tout l'intérêt d'avoir des interféromètres extrêmement stables.