Introduction
Encadrant: Médéric ARGENTINA,
Intervenant: Yann BOURET,
Janvier - Mai 2018

En décembre 2014, Médéric ARGENTINA et ses collègues ont publié un article intitulé " Scaling macroscopic aquatic locomotion ".
Ils ont notamment montré qu'une loi universelle régissait la locomotion aquatique des organismes marins, en fonction de leurs caractéristiques (tailles, amplitudes et fréquences de leurs nageoires). Ils ont aussi montré que ces lois etaient applicables à tout ces animaux malgré leurs différences de tailles ou de poids. Ils ont alors mis au point une loi dites "d'échelle".
Au cours de notre projet nous aurons alors pour mission de retrouver certaines de leurs observations et decouvertes sur ce sujet.
Pour mener à bien nos expériences nous utiliserons principalement:
- un tunnel hydrodynamique qui servira de zone d'étude.
- ainsi qu'un poisson robotisé, fabriqué grâce à une imprimante 3D à partir de polymères.
Ce poisson sera également animé par un servomoteur, relié directement à sa nageoire à l'aide de fil de pêche, qui nous permettra de faire varier, grâce à un programme, son amplitude et sa fréquence d'excitation. Ce poisson sera également relié à une tige munie de capteur de force ce qui nous permettra de relever des données exploitables essentielles.
Sachant que pour se mouvoir un poisson a besoin de déplacer un volume d'eau équivalent à son propre volume on s'appliquera à mesurer les forces hydrodynamiques qui agissent sur celui-ci pour différentes conditions afin d'en deduire les champs de vitesse. Pour cela on fera varier la vitesse d'écoulement dans la veine, qui simulera un courant laminaire de l'eau, ainsi que la fréquence et l'amplitude de la queue du poisson.
On cherchera alors à trouver le bon couple fréquence/amplitude de la nageoire, pour chaque fréquence d'excitation de la veine, où le poisson sera capable d'avancer comme dans une situation réelle.
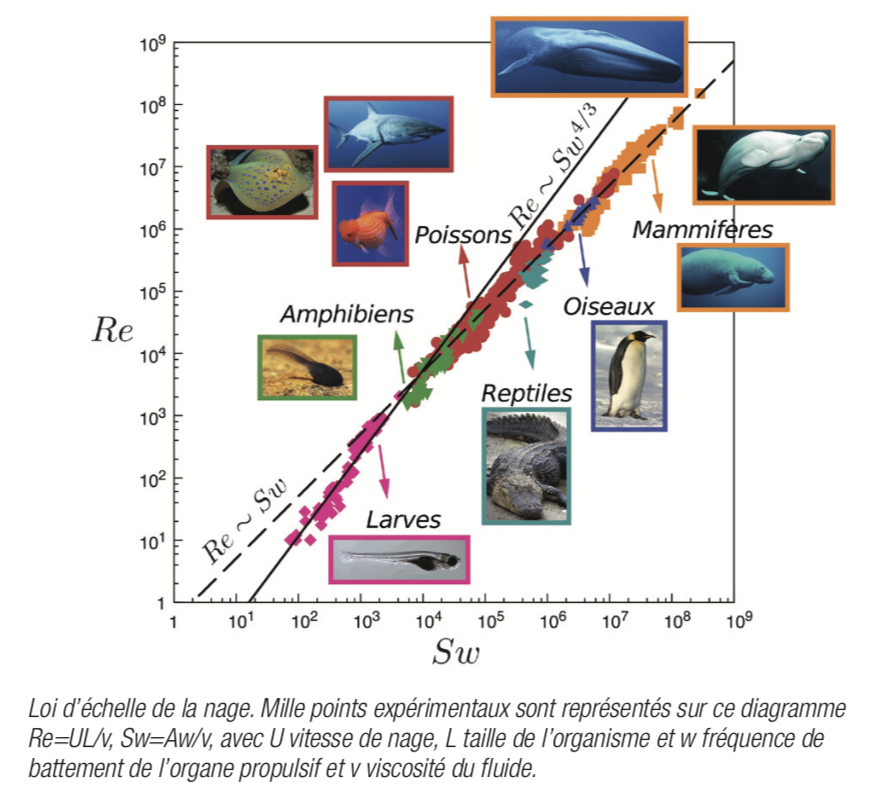
Voici l'illustration qui résume l'ensemble des travaux de monsieur ARGENTINA. Elle représente la vitesse de nage en fontion du couple amplitude/fréquence de battement de la nageoire pour 1000 animaux.
Lien de l'article ici.
Expériences
Nous présentons l'ensemble de nos précédents travaux ainsi que la liste intégrale du matériel que nous avons utilisé dans notre rapport de mi-projet

Mesure des champs de vitesse
Cette partie consiste à mesurer l'écoulement de l'eau dans la veine avec ou sans le poisson (qui est lui même immobile ou en mouvement). Nous avons utilisé deux méthodes:
-Une méthode approximative par l'utilisation du colorant.
-Une autre bien plus précise avec l'utilisation de la méthode P.I.V (Particle Image Velocimetry).
Vérification de la fiabilité du servomoteur
Nous avons décidé de verifier que la fréquence imposée par le programme informatique était capable d'être suivie par le servomoteur. Pour cela, on décide de sortir le poisson de l'eau afin de limiter toute altération de mesure causée par le frottement avec le liquide. Après deux series de mesures nous validons le fait que la fréquence est bien controllée, comme en témoigne les deux graphes suivants pour les amplitudes de 10° et 20°.
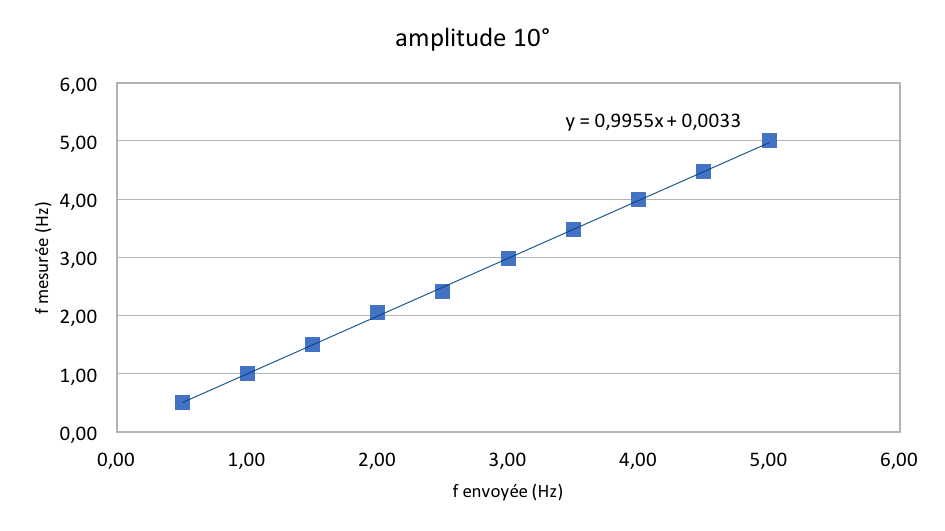
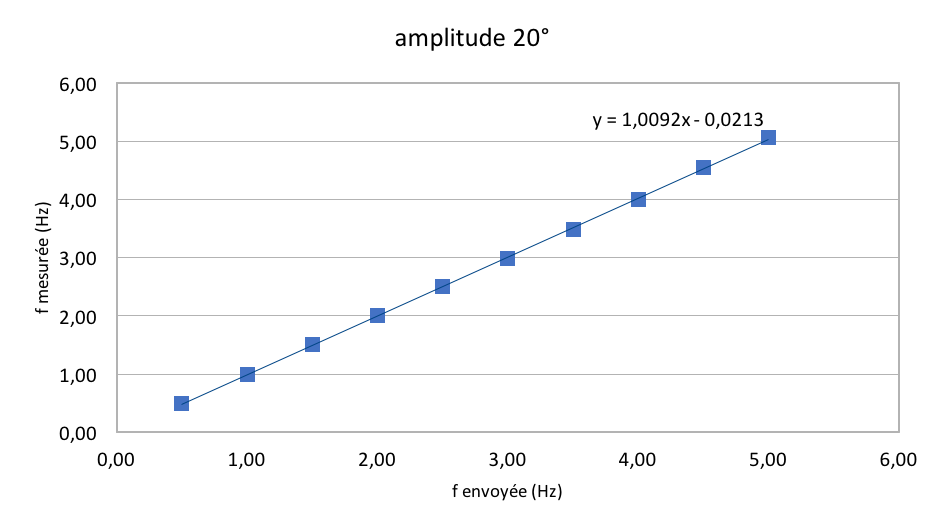
Lien entre l'amplitude et la fréquence.
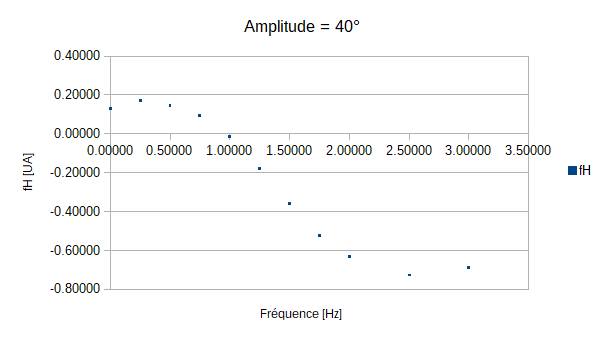
Cependant, nous pouvons nous interoger sur la question suivante: est-ce que le servomoteur réplique la bonne amplitude de la fréquence ?. La réponse est non et nous le montrons à l'aide de nos mesures:
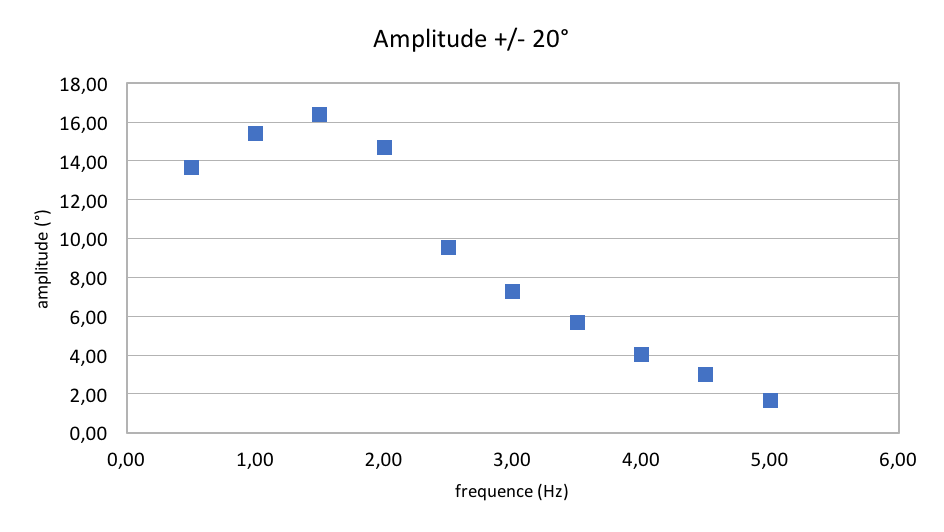 Nous pouvons observer dans un premier temps qu'il faut atteindre une certaine fréquence pour trouver l'amplitude souhaitée, bien que nous ne l'atteignions pas. Ensuite, l'amplitude décroit car la fréquence est bien trop élevée pour que le poisson suive en amplitude. On observe un phénomène de résonance.
Nous pouvons observer dans un premier temps qu'il faut atteindre une certaine fréquence pour trouver l'amplitude souhaitée, bien que nous ne l'atteignions pas. Ensuite, l'amplitude décroit car la fréquence est bien trop élevée pour que le poisson suive en amplitude. On observe un phénomène de résonance.
En conséquence, on utilisera un intervalle compris entre 0 et 3 Hz lors de nos expériences afin de limiter cet effet.
Des notices d'utilisations sont disponibles dans la rubrique Annexe.
Mesure de l'amplitude, de la fréquence de la nageoire et de la force hydrodynamique.
Nous allons ici tâcher de mettre en évidence les liens existants entre l'amplitude (exprimée en cm) de la queue et sa fréquence d'excitation (exprimé en Hz). On mesurera également la force hydrodynamique, fH (exprimé en Unité Adimensionnée), ressentie par le poisson afin d'exprimer l'ensemble de nos acquisitions en fonction de la fréquence et de l'amplitude. Il est important de noter qu'il s'agit bien d'une force hydrodynamique et non d'une force de trainée, en effet bien que ce soit une force que le poisson subit, lorsqu'il est en mouvement, on ne peut pas assurer qu'il n'y ait que la force de trainée qui rentre en jeu.
On mesurera l'amplitude précise à l'aide de l'outil P.F.V., en effet nous ne pouvons pas utiliser l'amplitude imposée au servomoteur car la dimension n'est pas bonne (nous souhaitons travailler avec des centimètres plutôt qu'avec des degrés) et, de plus, nous avions prouvé précédemment qu'il existait un facteur entre l'amplitude demandée au servomoteur et l'amplitude effectuée par la nageoire.
Cette observation est disponible dans la partie 4.5 de notre rapport .
On tracera alors l'ensemble de nos acquisitions à l'aide de graphe:
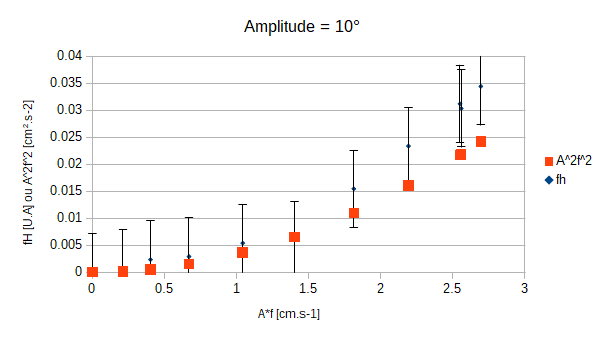
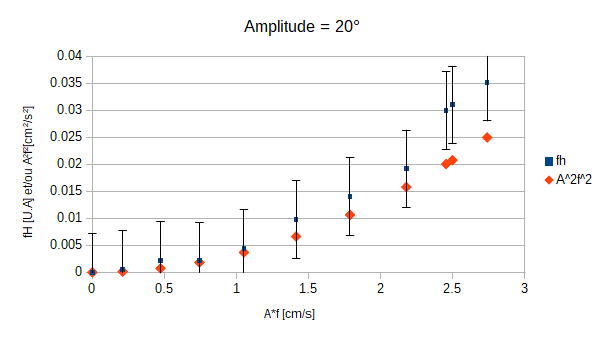
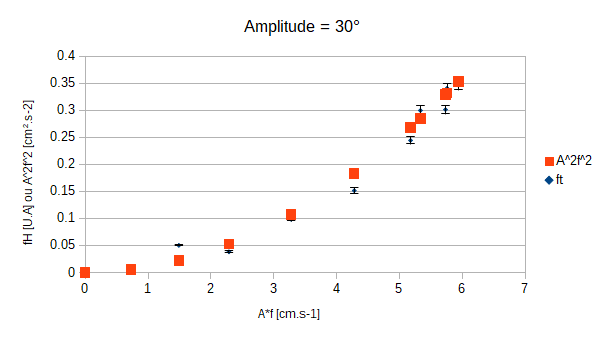
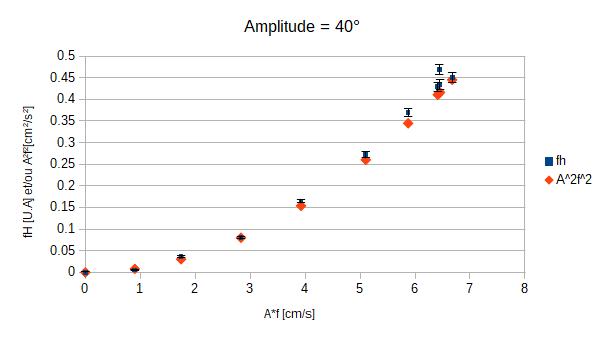
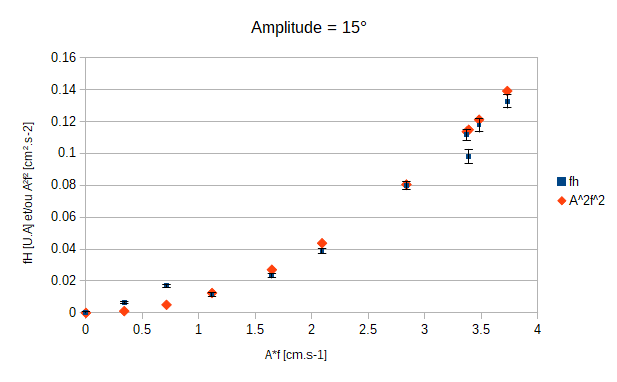
- A2×f2 et fH en fonction de A×f pour montrer que fH est proportionnelle à A2×f2 à un facteur près.
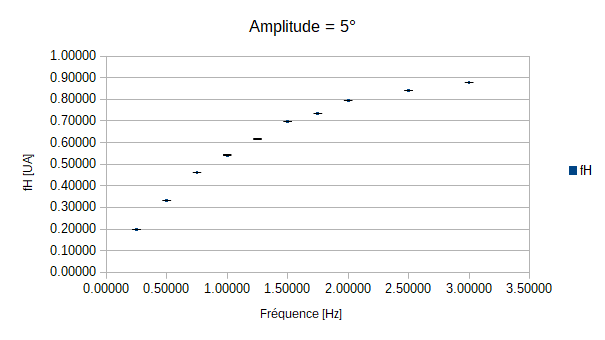
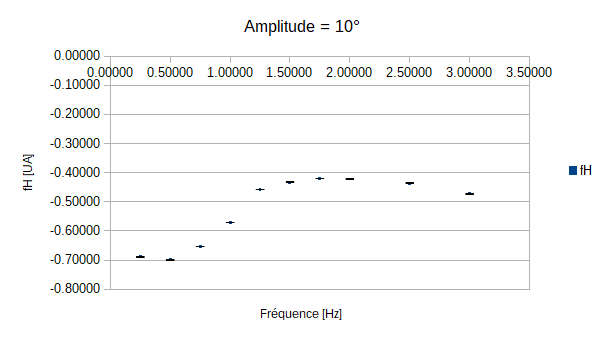
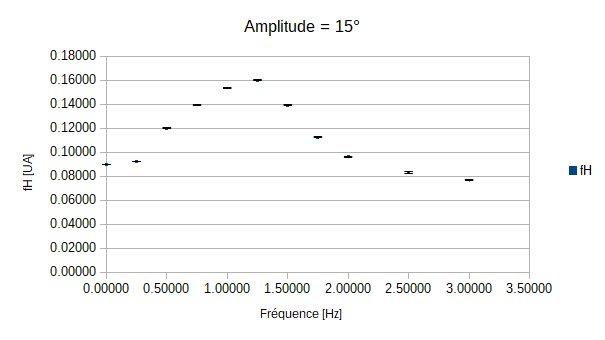
- fH en fonction de l'excitation de la nageoire (f) afin de déterminer la fréquence d'excitation de la nageoire nécessaire au poisson pour rester immobile dans la veine à une amplitude donnée.
Par la suite nous nous sommes aussi intéressés à trouver les couples fréquences/amplitudes de la nageoire adéquats pour lesquels le poisson reste sur place en fonction des différentes vitesses d'écoulement dans la veine. On tracera alors ce résultat à l'aide d'un graphe en 3 dimension.
Les courbes sont disponibles dans la rubrique Résultats.
Mesure à l'aide de la méthode P.I.V sur un cylindre.


Pendant notre expérience du vendredi 18/05/2018, notre poisson a subit une défaillance. Ce jour là, nous avions alors contacté notre encadrant, monsieur ARGENTINA, qui était ce jour là en déplacemlent professionnel et avions essayé, en vain, de trouver une solution à ce problème. Nous n'avions malheureusement pas réussi et nous avions alors été contraint d'arrêter nos mesures. Le lundi suivant, le 22/05/2018, monsieur ARGENTINA nous proposa d'effectuer de nouvelles mesures à, l'aide de la méthode P.I.V., sur un cylindre.
L'ensemble de nos observations est disponible dans la rubrique Résultats.
Résultats
Dans ce chapitre, nous allons exposer tout les résultats des expériences menées précédemment. De nombreux graphes seront disponibles et commentés afin de montrer et expliquer ce que nous avons obtenu.
Mesure des champs de vitesse.
Bien que nous ayons déjà mentionné cette partie dans notre rapport de mi-projet, il nous a semblé essentiel de le commenter à nouveau car il s'agit de l'élément central du projet. Ces mesures sont les bases de notre travail.
Le but ici est de mesurer le champ de vitesse de l'eau dans la veine qui sera comparable, par exemple, à un courant d'eau subit par n'importe quel poisson. Pour cela deux méthodes s'offrent à nous:
La méthode du colorant.
L'utilisation du colorant va nous permettre d'obtenir qualitativement la vitesse d'écoulement du fluide dans la veine en fonction de la fréquence d'excitation de la pompe. Pour cela, munis de nos téléphones portables, nous avons enregistré des vidéos durant lesquelles des gouttes de colorants, que nous avions préalablement deposées, traversaient la zone d'étude de la veine (zone d'écoulement quasi-laminaire). A l'aide d'une feuille de papier millimetrée scotchée à la paroie vitrée de la veine nous avons mesurée une distance, qui, associée au temps des passage des gouttelettes, nous a permis d'en déduire des vitesses approximatives.
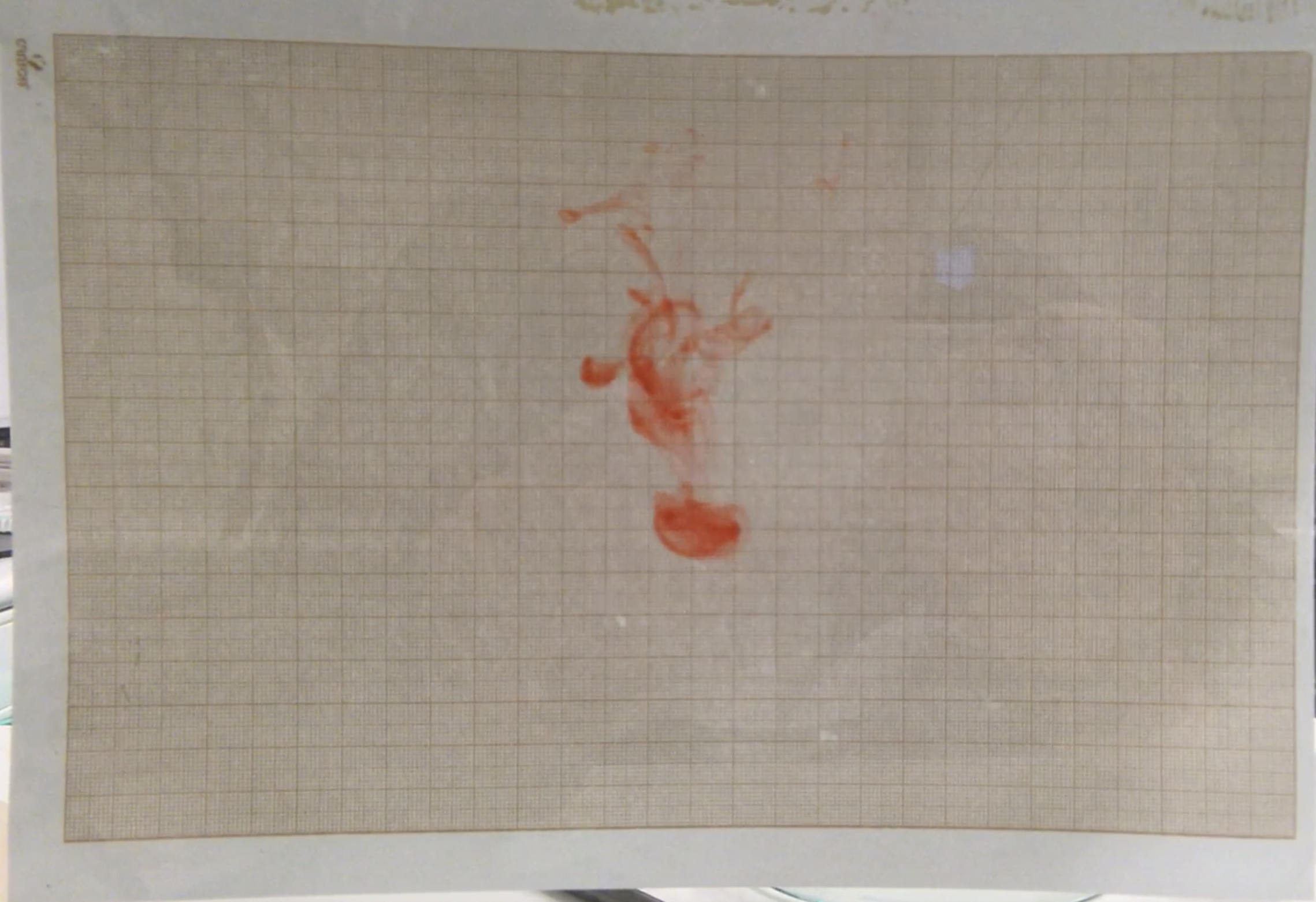
A l'aide de cette expérience, nous avons déduit une vitesse d'environ 12cm.s-1 pour une fréquence de pompe de 50Hz.
La méthode P.I.V.
A présent, on s'applique à obtenir des valeurs beaucoup plus précises, pour cela on utilise la méthode P.I.V.. Pour se faire, nous avons besoin du logiciel PFV Photron FastCam Viewer, d'une camera, des particules et d'une nappe laser. On dispose la caméra au dessus de la veine afin qu'elle puisse enregistrer le parcours des particules, éclairées par le laser. A l'aide du logiciel PIVLab, issu du programme Matlab, nous traitons les données afin de calculer les vitesses d'écoulements.
Pour plus de détail sur le matériel, le montage et les méthodes d'utilisations des différents logiciels vous pouvez vous réferer à notre rapport de mi-projet, partie 2.1, 2.2, 3.1 et son annexe.
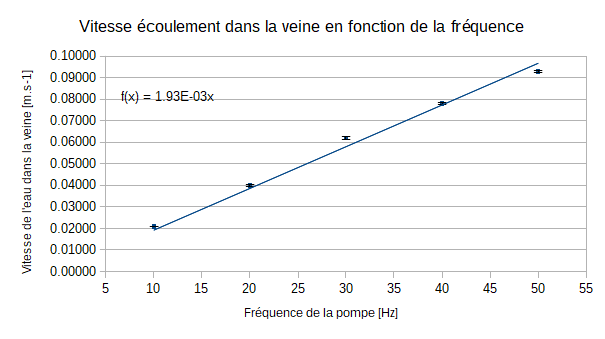
On constate grâce à la méthode P.I.V que l'ordre de grandeur est respecté par rapport à la méthode avec le colorant. L'avantage de cette méthode, malgré le fait qu'elle soit plus longue, est que nous pouvons obtenir une incertitude sur les valeurs, ainsi que le champs de vitesse sur toute la zone de la nappe. On constate que la courbe est linéaire ce qui signifie que la vitesse d'écoulement de la veine est proportionnelle à la fréquence de la pompe.
A présent, on réitère la même expérience avec le même matériel et nous ajoutons le poisson dans la veine. A l'aide du programme arduino nous allons controler l'amplitude de sa queue. Cela nous permettra alors de constater si un obstacle interferre sur l'écoulement d'un fluide dans un milieu, ou non, et si la variation de son amplitude peut, elle aussi, modifier cet écoulement.
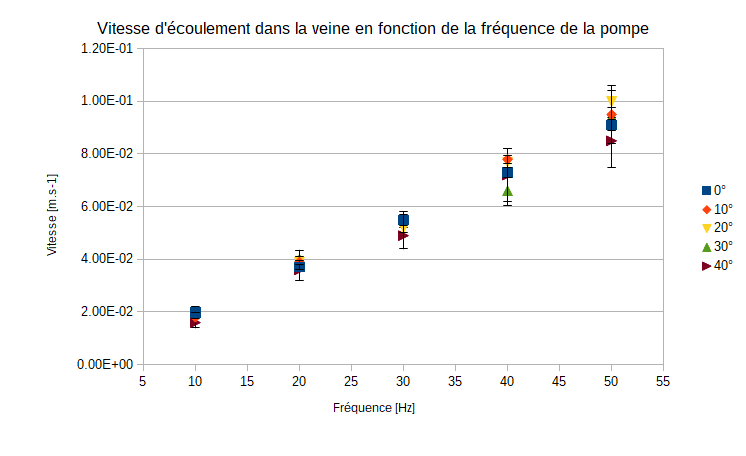
On constate que selon l'amplitude de la queue (0°,10°,20°,30°,40°) la vitesse d'écoulement du fluide est modifiée et diminue très faiblement (voir graphe). Cependant on remarque que la tendance est conservée quelque soit l'amplitude appliquée.
Mesure de l'amplitude , de la fréquence de la nageoire et de la force hydrodynamique.
Proportionnalité entre A2×f2 et fH.
Pour réaliser ces mesures nous allons devoir utiliser la veine hydrodynamique, le poisson relié au capteur de force, la caméra ainsi que le logiciel P.F.V. Photron FasTcam Viewer et tous les logiciels d'acquisitions (arduino et python).
Le montage principale est disponible dans notre rapport dans la partie 2.2, les références du matériels sont dans la partie 2.1 et une partie des programmes python et arduino sont dans l'annexe.
Nous allons montrer que si nous exprimons fH et A2×f2 en fonction de A × f alors ces deux quantités suivent la même tendance. Pour cela nous avons décidé, au début, d'effectuer des mesures pour quatre amplitudes differentes de la nageoire et la fréquence de la pompe bloqué à 0Hz (champ de vitesse nul).
Avant de commencer toute manipulation, il est important d'effectuer une vérification de la calibration de l'amplificateur (lien entre le capteur et le programme arduino). En effet il faut bien placer notre 0 de référence afin que nous ne finissions pas en dehors de la plage limite de l'arduino (compris entre 0 et 5 Volt). Etant donné que cette calibration peut être modifiée entre plusieurs expériences et/ou d'un jour à l'autre, nous tâcherons d'exprimer nos valeurs en unité adimensionnée plûtôt qu'en volt.
Il est également important d'effectuer une pause entre 2 series de mesures si l'amplificateur vient à être trop chaud: les valeurs pouvant être altérées et les amplificateurs pouvant être à leurs tours endommagés.
Par la suite, nous définissons une valeur référence entre chaque mesure de fH lorsque le poisson revient à son état initial (fréquence et amplitude nul), afin de la retrancher à la valeur suivante obtenue lors de nos aquisitions. En notant l'heure de la prise de chacune de ces valeurs références nous pouvons ainsi calculer la dérive de notre système. Nous trouvons une dérive approximative de 2.0 × 10-5 UA.s-1 lorsque le poisson est immobile et 1.0 × 10-5 UA.s-1 quand le poisson nage. Il est logique que la dérive de notre système soit moins grande quand le poisson nage car dans ces mesures là, la pompe n'est pas active. L'ensemble de ces calculs cherche à limiter les phénomènes d'hystérésis.
Après avoir multiplié nos valeurs par une constante d'harmonisation nous constatons d'ores et déjà que les tendances semblent similaires. Nous pouvons constater que nos erreurs sur les valeurs de fH sont conséquantes. Lorsque nous utilisions le programme python (disponible dans l'annexe de notre rapport) nous calculons l'écart-type moyen entre 1000 mesures par rapport à la valeur moyenne de ces même 1000 mesures. Cependant, après discussion avec M. BOURET, nous avons été informé qu'il était plus adéquat d'utiliser l'erreur standard. Pour l'obtenir il nous suffit juste de diviser notre écart-type moyen par la racine du nombre de mesures sur lesquelles nous moyennons nos valeurs; ici il suffira donc de diviser par racine de 1000.
À présent on constate que l'erreur obtenue est plus adéquate. Il est important de souligner qu'une série de mesure pour une amplitude donnée nécessite entre une heure et une heure trente de manipulations dans la mesure où tout se passe bien.
Suite à cette remarque nous décidons de rééditer une serie de mesure pour 15° (juste milieu entre 10° et 20°) afin d'obtenir, là aussi, un graphe cohérent pour ce qui est des erreurs.
Détermination de l'excitation de la nageoire nécéssaire pour que le poisson reste immobile à une amplitude donnée.
L'interêt de cette partie est de trouver les fréquences d'excitations de la nageoire pour lesquelles le poisson est dans un état stationnaire dans la veine. Pour cela on va faire varier trois paramètres en parallèles:
- la fréquence de la pompe qui déterminera la vitesse d'écoulement de l'eau dans la veine.
- l'amplitude de la queue.
- la fréquence d'excitation de la queue.
Pour cela on s'intéresse à mesurer la force hydrodynamique fH, en faisant varier la fréquence de la nageoire pour une excitation de la veine et une amplitude de la queue donnée. On utilisera alors tout le matériel lié à l'utilisation du poisson (carte arduinoMEGA et logiciel arduino, générateur de courant(celui pour le poisson)) et du capteur de force (tensiotron, un autre générateur de courant (celui pour le tensiotron), l'oscilloscope, le capteur de force, le logiciel python) et on fera attention à respecter les remarques que nous avons préalablement faites afin de limiter les erreurs et/ou d'éviter tout problème (dérive, calibration et controle de temperature du tensiotron).
On obtient les graphes suivant:
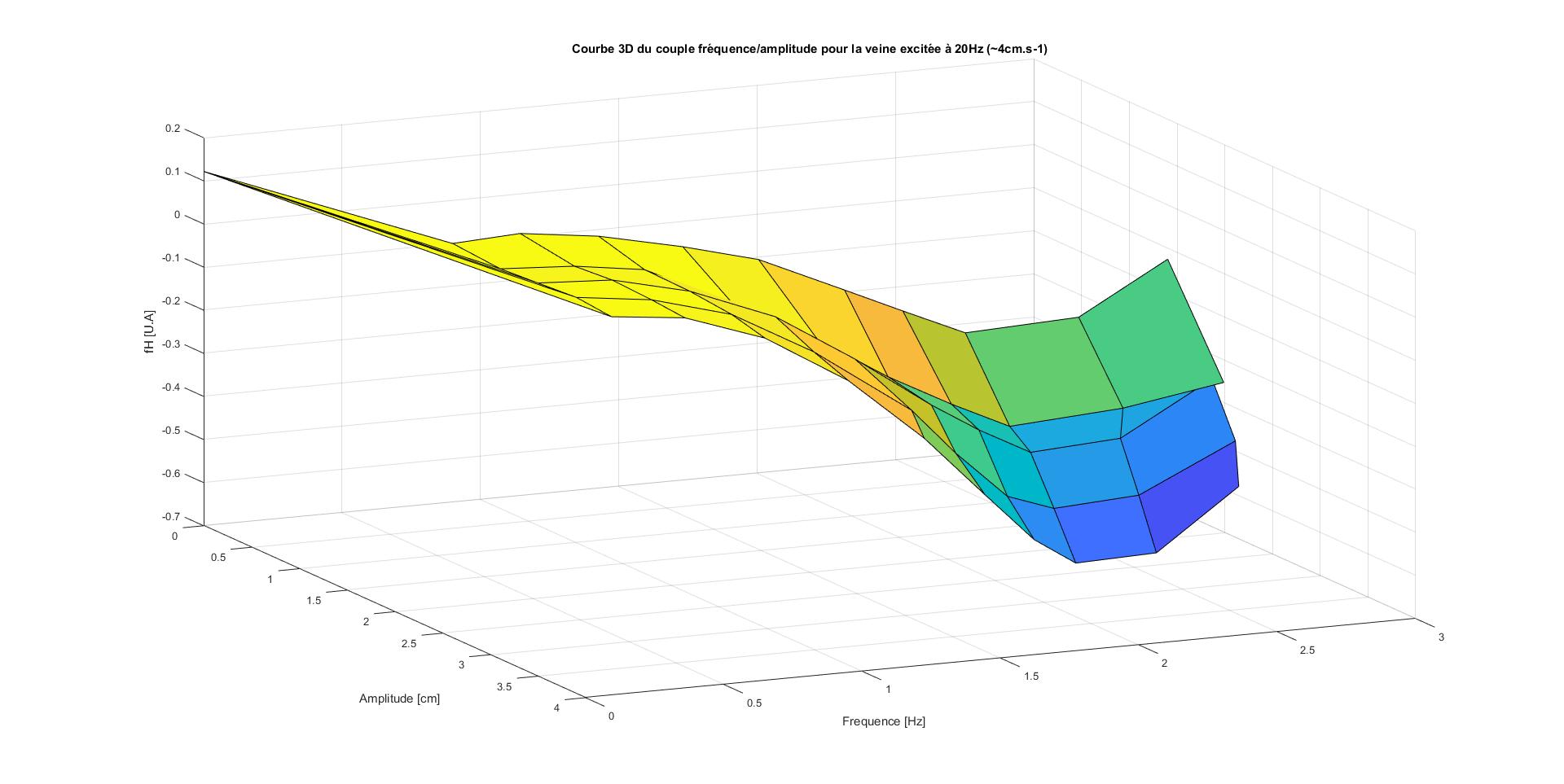
1° pour une excitation de la pompe à 20 Hz (soit un écoulement d'environ 4 cm.s-1 dans la veine)
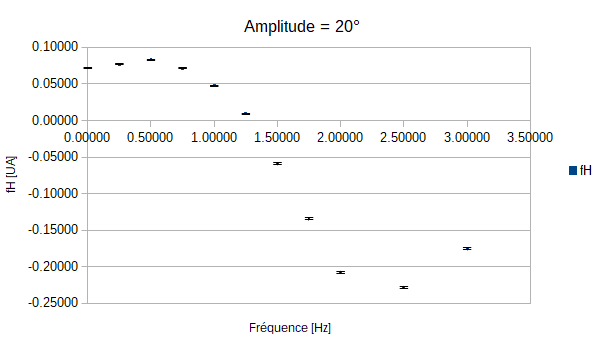
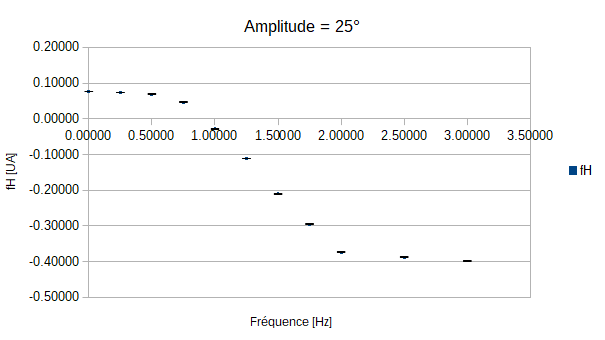
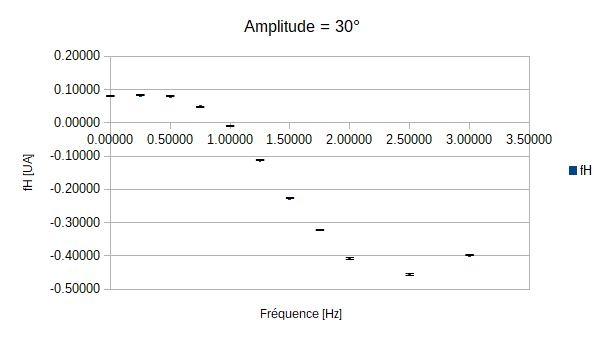
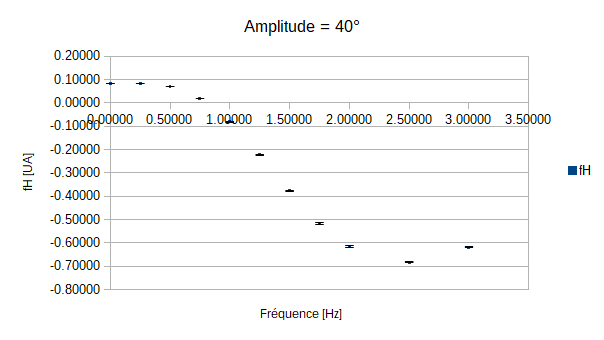
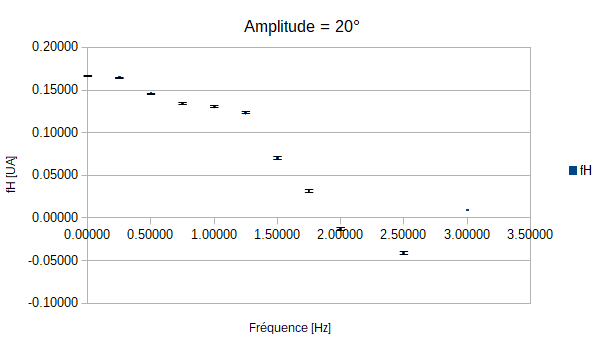
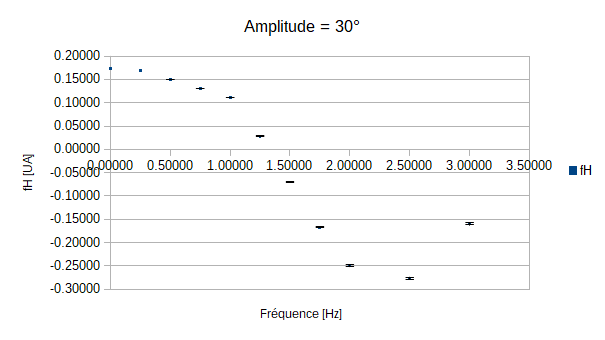
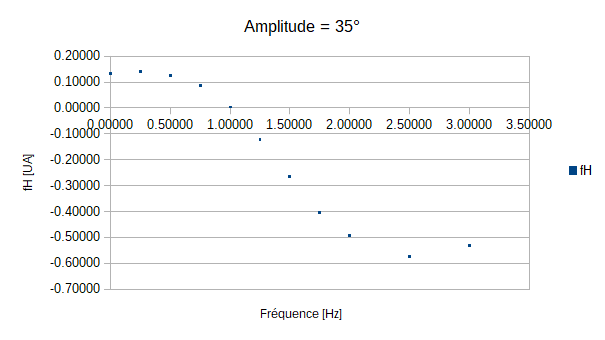
On constate que pour les amplitudes de 5°, 10° et 15° le poisson n'est jamais immobile quelque soit la fréquence de battement de sa queue. On peut expliquer cela par le fait que les amplitudes demandées soient trop faibles par rapport à l'écoulement exercé par la veine sur le poisson.
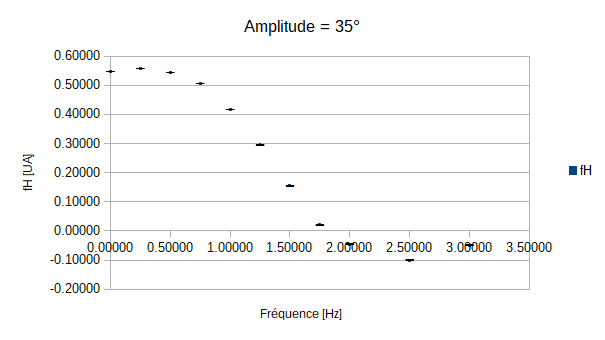
En revanche pour les autres mesures, on constate que lorsque l'amplitude augmente la fréquence nécessaire pour que le poisson soit stationnaire diminue. Cependant, le graphe qui correspond à l'amplitude de 35° ne semble pas obéir à cette règle.
Mais une explication toute simple est possible: en effet on remarque que plus les amplitudes et les fréquences augmentent, moins la queue respecte les instructions demandées. En effet lorsque les amplitudes et les fréquences vont croître, on observera que la nageoire ne va pas réaliser le mouvement complet car la fréquence devient trop grande, et donc la vitesse trop rapide. Ainsi la nageoire, bien qu'allant vite, ne balayera pas le même volume d'eau, le rendement en sera alors affecté: on parlera alors d'efficacité de la nage.
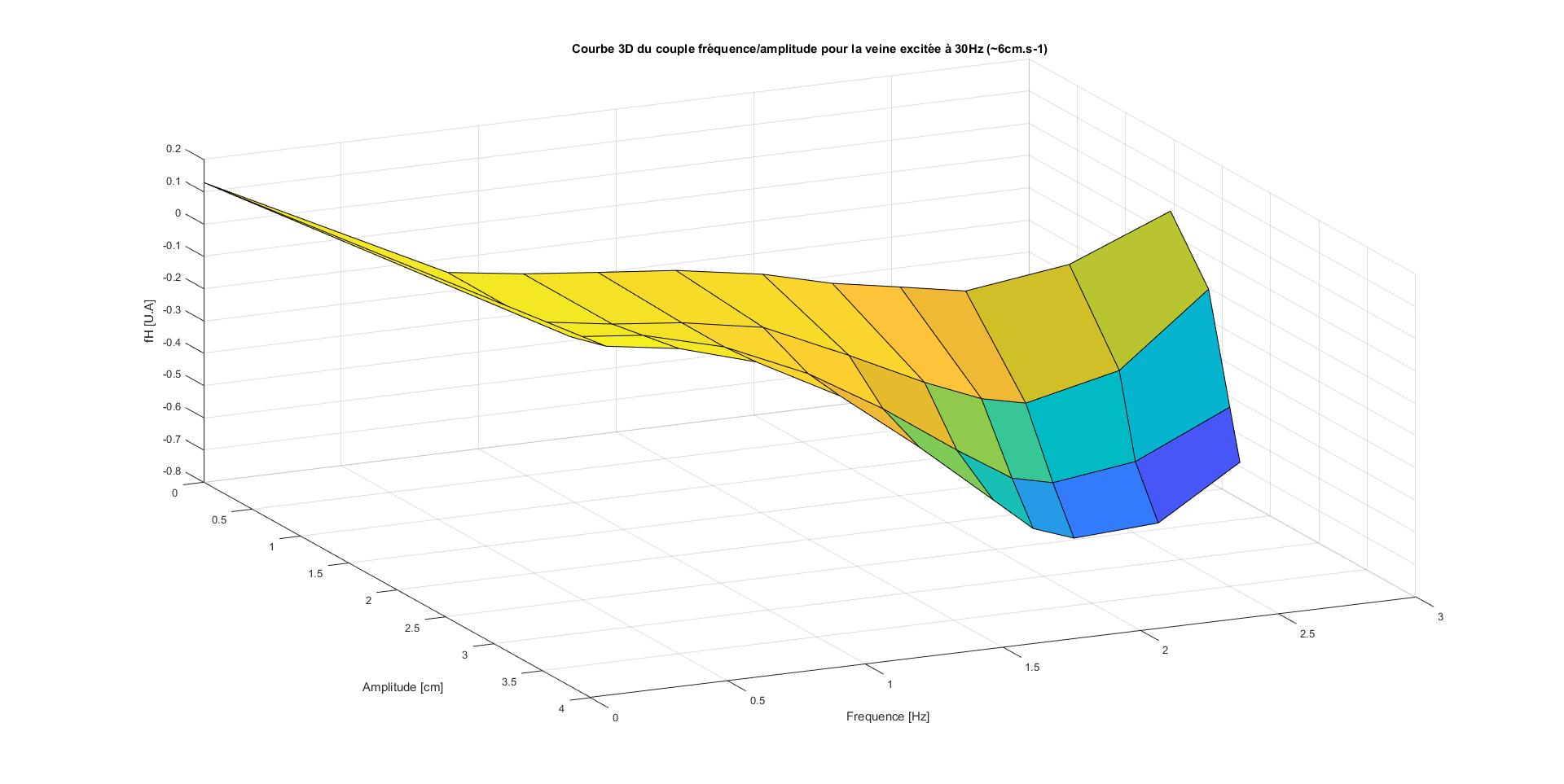
2° pour une excitation de la pompe à 30 Hz (soit un écoulement d'environ 6 cm.s-1 dans la veine)
En comparaison avec les graphes pour une excitation de la pompe à 20 Hz, nous observons le même comportement. En effet plus l'amplitude augmente plus la fréquence demandée pour que le poisson soit stationnaire diminue. De plus, en faisant le parallèle avec les précédents graphes, par exemple si on compare ceux obtenus pour une amplitude de 20°, 30° et 40° entre l'écoulement à 4 cm.s-1 et 6 cm.s-1 dans la veine, on peut voir que la fréquence d'excitation de la nageoire nécessaire pour que le poisson soit immobile augmente lorsque l'écoulement dans la veine augmente.
Cette observation nous semble logique et nous soutient dans l'idée que nos mesures sont correctes.
Détermination du couple fréquence/amplitude de la nageoire pour que le poisson reste immobile.
Cette fois ci le principe est exactement le même, sauf que nous mesurons en plus l'amplitude de la queue grâce à la caméra. En effet jusqu'à présent nous utilisions seulement l'amplitude théorique que nous entrions dans la console arduino tandis que maintenant nous allons utiliser l'amplitude que nous mesurons en cm.
Les mesures seront donc beaucoup plus précises et nous observerons bien le phénomène que nous avons expliqué, dans la partie expérience, au sujet des limites du servomoteur sur la retransmission des amplitudes en fonction de la fréquence d'excitation. Vous pouvez voir ci-dessous un des exemples de valeur issue de la mesure avec la pompe à 30 Hz et l'amplitude du poisson exigée à 20°.
On constate bien que les amplitudes augmentent entre les différentes fréquences de la queue allant de 0 Hz à 1,50 Hz puis décroissent.
Remarque: Comme vous pouvez le voir sur notre tableau Excel, le battement de la queue du poisson est défini par une valeur réfèrence à laquelle on ajoute ou on retranche l'amplitude souhaitée. Ici, l'alignement de la queue avec le poisson dans la veine est obtenu pour un angle de 108° dans la console arduino. La valeur théorique aurait du être 90° mais nous avons constaté qu'il existait un petit décalage.
Nous obtenons les graphes suivant:
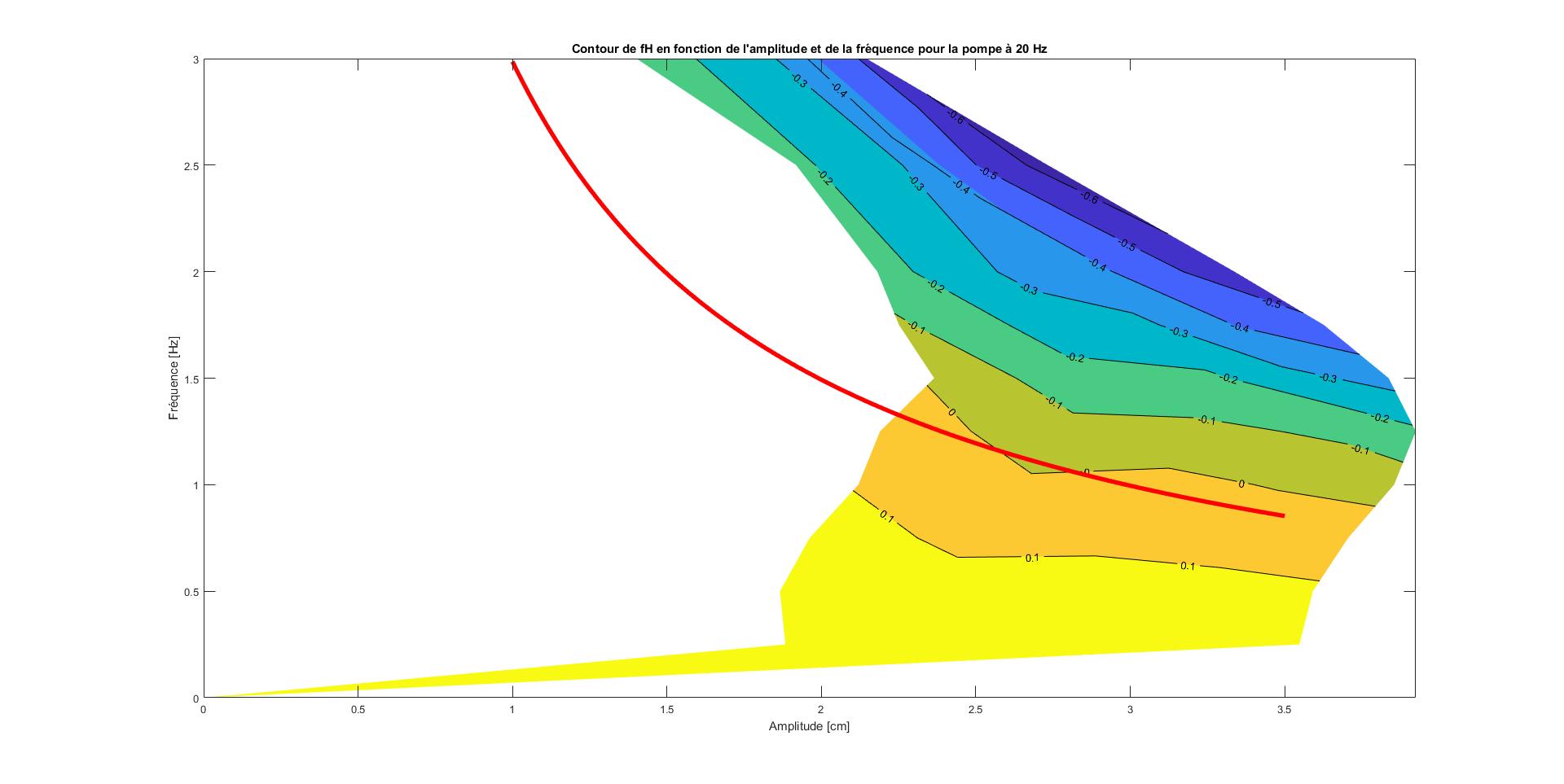
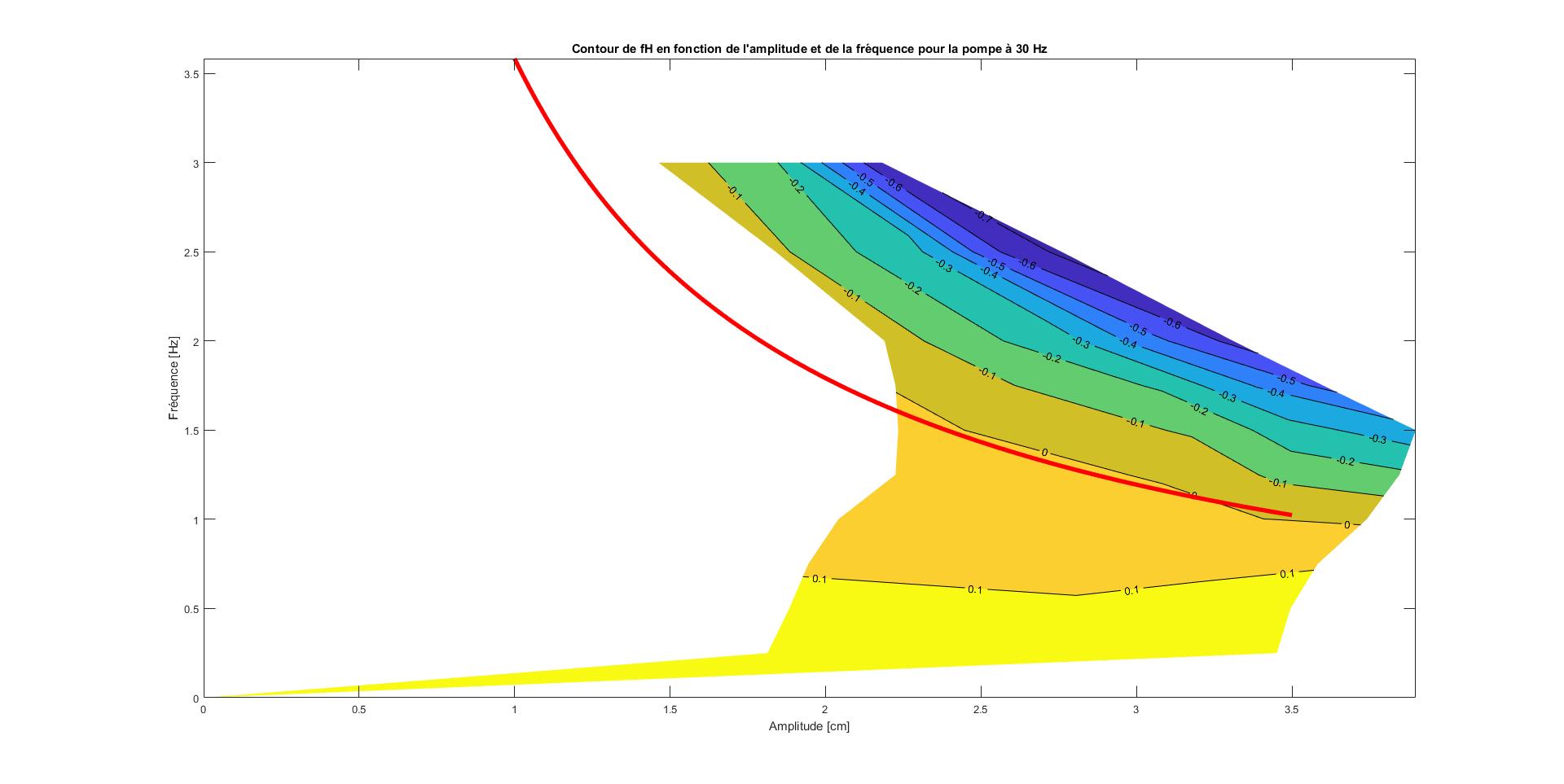
Par soucis de clareté et de compréhension nous décidons de retracer ces courbes en utilisant la fonction "contourf". Cette fonction nous permet d'aplanir le graphe en 2 dimensions et de conserver la troisième dimension (la force hydrodynamique) à l'aide d'une légende de couleur (plus la couleur tend vers le bleu foncé plus la force est petite).
On obtient les graphes suivant:
Une notice d'utilisation de MathLab est disponible en Annexe.
Sur ces 2 figures, on observe la force exprimée sur des graphes amplitude/fréquence sur lesquels on montre le passage en 0 de la force hydrodynamique ainsi que la courbe de tendance de la loi universelle. Depuis celle-ci on peut voir que nos mesures sont en accord avec la loi trouvée par monsieur ARGENTINA à un facteur près. De cela on peut en découler que notre poisson robotisé nage moins vite.
Si le couple du poisson robotisé se trouve dans la partie au-dessus de la courbe de tendance alors il avance, s'il est en dessous, il recule et s'il est sur la courbe alors il est immobile.
Mesure à l'aide de la méthode P.I.V sur un cylindre.
Nos nouvelles mesures de P.I.V. ont servi à mettre en évidence l'appartition de tourbillons, que nous apercevions déjà brièvement à l'oeil nu, à la suite de l'obstacle placé dans la veine hydrodynamique.
Vous avez à votre disposition les deux vidéos ci-dessous qui représentent le champ de vitesse et la localisation des tourbillons dans l'écoulement après notre cylindre.
- vidéo du champ de vitesse pour la pompe à 25 Hz.
- vidéo de localisation des vortex pour la pompe à 25 Hz.
Légende:
- Pour la vidéo du champ de vitesse: on dispose d'une echelle décroissante entre les couleurs chaudes et froides; plus la couleur est chaude plus l'écoulement est rapide.
- Pour la vidéo de localisation des tourbillons: on dispose de la même échelle; plus la couleur est chaude plus l'intensité du tourbillons est forte.
Remarque: la vidéo de la vorticité est obtenu grâce à celle du champ de vitesse. Il s'agit des mêmes données auxquelles nous avons effectué un nouveau traitement suivi d'un retranchement, à tout les points, de la valeur moyenne du champ de vitesse.
Annexe

Voici notre rapport de mi-projet à télécharger en cliquant ici !
Glossaire
- résonance : phénomène selon lequel certains systèmes physiques (électriques, mécaniques...) sont sensibles à certaines fréquences.
- hystérésis :
phénomène traduisant le fait que la grandeur mesurée dépend de l'historique de l'expérience. Nous avons observé ce phénomène losrque dans nos manipulations nous nous apercevions que notre système subissait un décalage entre deux répétitions d'une même mesure: c'est ce qu'on a appelé la dérive.
Notice d'utilisation.
Dans cette section on détaillera, comme nous l'avons fait dans notre rapport, certaines des méthodes que nous avons utilisé pour effectuer nos mesures.
Pour le premier nous allons expliquer comment nous avons mesuré la fréquence d'excitation de la nageoire.
On indique au programme la fréquence souhaitée puis à l'aide de nos téléphones on enregistre des vidéos. Celles-ci sont envoyées dans notre ordinateur personnel à l'aide de la fonction AirDrop. Par la suite nous les traitons à l'aide du logiciel iMovie grâce auquel nous avons obtenu des mesures de temps précise afin d'en déduire la fréquence. (f = 1/T).
Pour le deuxième il s'agit d'expliquer comment nous avons calculé l'amplitude de la nageoire.
On enregistre une petite période du mouvement à l'aide de la caméra grâce au logiciel P.F.V. et en utilisant l'outil pointeur on sélectionne le début et la fin du mouvement de la nageoire en prenant un même point de référence.
On obtient alors une distance exprimée en pixel.
À l'aide d'une règle graduée on établit un calibrage afin de convertir cette distance en cm (remarque: 570,8 pixels = 5 cms).
On obtiendra alors une amplitude exprimée en cm en fonction de l'amplitude que l'on a ordonné au servomoteur par le biais du programme arduino.
Précédemment nous avions d'ailleurs montré qu'il existait un lien entre l'amplitude demandée au servomoteur et celui effectuée par la nageoire. Pour plus de détail se référer à la partie 4.5 de notre rapport .
Pour le troisième il s'agit d'expliquer comment nous avons utilisé MathLab pour tracer nos courbes en 3 dimension.
Pour les graphiques 3D et "contourf":
- On ajuste toutes nos valeurs de fH afin d'avoir la même force d'origine (on fera attention à bien commencer avec une fH > 0,1 U.A afin de bien modéliser la force car sinon le logiciel MathLab n'imprime pas bien nos valeurs).
- On place nos valeurs d'amplitudes, de fréquences et de forces dans des matrices qu'on nommera respectivement Acm, f et fH. Chaque valeur Mij d'une matrice est reliée aux autres valeurs Mij des deux autres matrices.
- Sur MathLab, à l'aide de la fonction "surf(Acm,f,fH)" et "contourf(Acm,f,fH)" on peut imprimer notre courbe en 3D ainsi que notre contour exprimés en fonction des axes amplitudes et fréquences.
- L'équation de la loi universelle de la nage nous a été donné par monsieur ARGENTINA:
U = 0,4×ω×A avec ω = 2π×f.
- On fait apparaître la courbe de cette loi sur notre contour afin de vérifier la fiabilité de nos mesures. Pour cela on ressort l'équation suivante: f = U/(0,4×2πA) = 12,5/(2πA). Avec U la vitesse de l'écoulement dans la veine (soit 5 cm.s-1 pour la pompe à 20 Hz et 6 cm.s-1 pour la pompe à 30 Hz).
Remarque: les valeurs de U ci-dessus correspondent aux valeurs données par monsieur ARGENTINA et non celles que nous avions trouvé.
- La tendance de notre contour doit être similaire à celle que l'on ajoute et doit se superposer à notre ligne de 0 des forces.
Pour cela on a du ajuster notre courbe grâce à un facteur égale à 1.5 pour les faire coincider. De ce facteur nous pouvons émettre le postulat que notre robot se déplace 1.5 fois moins vite qu'un réel poisson.
Contact
- Cliquez sur le nom de la personne que vous souhaitez contacter !
Remerciements
Nous tenions à remercier notre encadrant monsieur Médéric ARGENTINA ainsi que son collègue de recherche monsieur Yann BOURET pour tout le temps et l'aide qu'ils nous ont accordé et apporté tout du long de notre stage.
Tout les travaux d'experimentations réalisés au cours du projet n'ont pas souvent été facile mais leurs connaissances ainsi que leurs patiences nous ont toujours permis d'avancer et de mener à bien notre étude.
Nos remerciements s'adressent aussi à madame DOYA, qui nous a attribué le projet et qui a toujours été présente pour répondre à nos moindres questions.
Elements
Text
This is bold and this is strong. This is italic and this is emphasized.
This is superscript text and this is subscript text.
This is underlined and this is code: for (;;) { ... }. Finally, this is a link.
Heading Level 2
Heading Level 3
Heading Level 4
Heading Level 5
Heading Level 6
Blockquote
Fringilla nisl. Donec accumsan interdum nisi, quis tincidunt felis sagittis eget tempus euismod. Vestibulum ante ipsum primis in faucibus vestibulum. Blandit adipiscing eu felis iaculis volutpat ac adipiscing accumsan faucibus. Vestibulum ante ipsum primis in faucibus lorem ipsum dolor sit amet nullam adipiscing eu felis.
Preformatted
i = 0;
while (!deck.isInOrder()) {
print 'Iteration ' + i;
deck.shuffle();
i++;
}
print 'It took ' + i + ' iterations to sort the deck.';
Lists
Unordered
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Alternate
- Dolor pulvinar etiam.
- Sagittis adipiscing.
- Felis enim feugiat.
Ordered
- Dolor pulvinar etiam.
- Etiam vel felis viverra.
- Felis enim feugiat.
- Dolor pulvinar etiam.
- Etiam vel felis lorem.
- Felis enim et feugiat.
Icons
Actions
Table
Default
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |
Alternate
| Name |
Description |
Price |
| Item One |
Ante turpis integer aliquet porttitor. |
29.99 |
| Item Two |
Vis ac commodo adipiscing arcu aliquet. |
19.99 |
| Item Three |
Morbi faucibus arcu accumsan lorem. |
29.99 |
| Item Four |
Vitae integer tempus condimentum. |
19.99 |
| Item Five |
Ante turpis integer aliquet porttitor. |
29.99 |
|
100.00 |