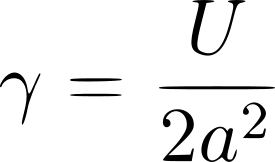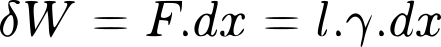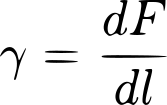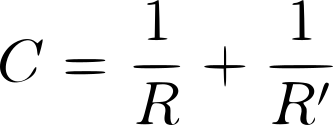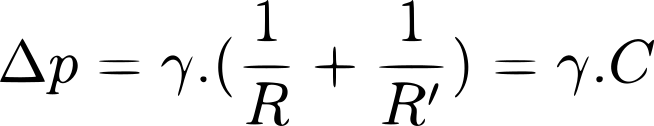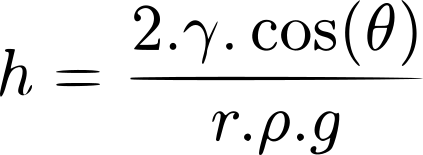Energie aux interfaces

Tension de surface

On observe une interface à la surface du liquide. Cette interface explique par exemple pourquoi certains insectes peuvent "marcher sur l'eau".
La tension de surface et la création d'une interface nécessitent un coût énergétique élevé. La tension superficielle caractérise une interface.
Elle change pour chaque interaction entre un liquide et un gaz ou entre deux liquides. Elle est unique et propre à la matière. On modélise ce phénomène avec les relations suivantes.
Si on considère U l'énergie de cohésion par molécule à la surface, chaque molécule perd à peu près la moitié de son énergie donc ¹⁄₂ U. On obtient alors une tension de surface :

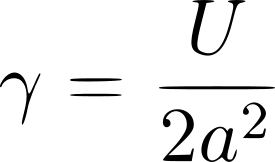
Avec a² la surface exposée par la molécule. On remarque que lorsque la tension de surface augmente, les interactions attractives entre molécules sont plus fortes. . On observe cette grandeur à l'échelle macroscopique. Pour se faire, on réalise par exemple, une expérience avec un trombone que nous posons sur la surface de l'eau: nous remarquons qu'il ne flotte pas mais repose bien sur une interface.

(Voir vidéo associée dans l'onget "Nos expériences")

Force capillaire

La déformation du fluide demande beaucoup d'énergie. Il adopte des formes qui minimisent cette énergie selon de nombreuses contraintes. C'est pour cela que les liquides ont tendance à prendre une forme de bulle car la sphère demande le moins d'énergie. La surface se crée par un apport d'énergie mécanique. Si on augmente la surface du liquide on le déforme. Le travail sera proportionnel au nombre de molécules nécessaires et donc proportionnel à la déformation. Nous supposons que la force est constante pour un allongement. On a :

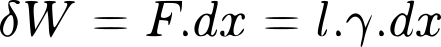
avec dx, F correspondant respectivement à l'allongement et la force tension superficielle.
On peut également définir la tension de surface γ telle que :

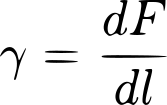
γ s'exprime en N/m²
Ainsi, la tension de surface représente une force par unité de longueur ou encore une énergie à fournir pour augmenter la surface d'une unité. On peut donc définir les forces capillaires qui sont:
- perpendiculaires en chaque point du contour.
- tangentes à l'interface.
- réparties de manière uniforme.

(Voir onglet "Nos expériences" pour la mise en évidence de ces forces)

Théorème de Young Laplace

La courbure de la surface est définie comme la courbure d'un objet géométrique. Elle est représentée par la mesure quantitative du caractère plus ou moins courbée de cet objet , à partir des deux principaux rayons de courbures R et R'.

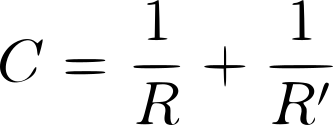
Le théorème permet le calcul de la différence de pression entre deux interfaces. Pour une surface quelconque on a ∆p qui est égal au produit de la tension superficielle par la courbure de la surface.

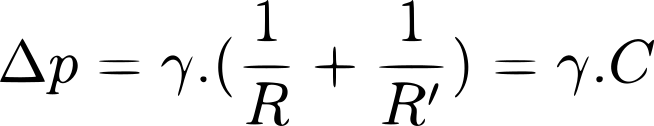
γ s'exprime en N/m
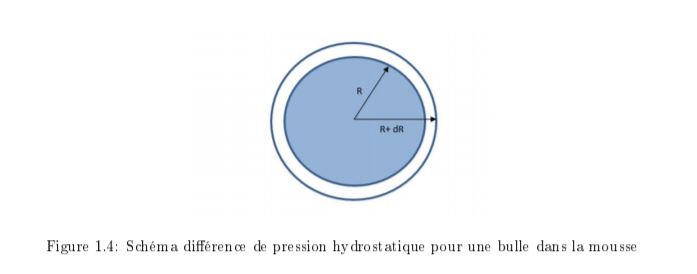
C étant la courbure de la surface et γ la tension superficielle. Si on s'intéresse à une bulle dans de la mousse on obtient :

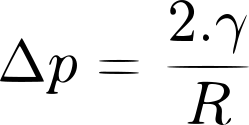
Dans l'expression on a un facteur 2 car R = R' , c'est une sphère avec un seul rayon de courbure

(Voir onglet "Nos experiences" sur la minimisation de surface)

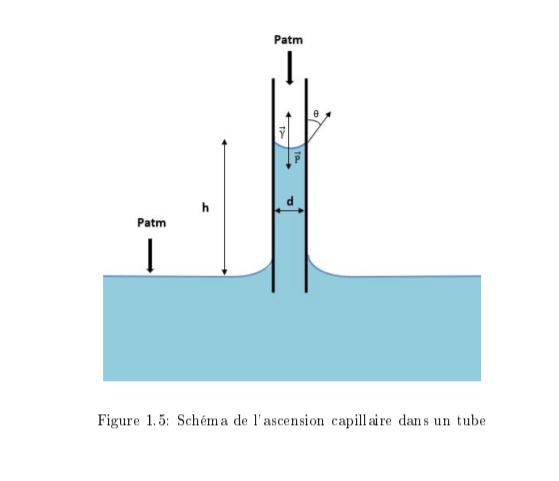
Ascension capillaire

L'ascension capillaire s'observe lorsqu' un fluide s'élève dans un tube plus ou moins mince. La loi de Jurin énoncée au XVIII ème siècle établit le lien entre hauteur du fluide, la tension de surface ainsi que l'angle de contact. On constate la formation d'un ménisque quasi-cylindrique s'accompagnant d'une surpression ∆p dans le gaz. Les forces capillaires sont responsables de l'ascension capillaire. On retrouve la loi de Jurin en se plaçant à l'équilibre des forces. Deux forces se compensent :
- les forces de tensions superficielles : F = 2.l.σ
- le poids du liquide qui s'est élevé : P = ρ.h.l.e.
On a donc la hauteur d'ascension :

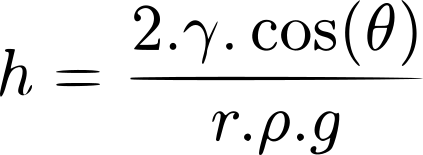
On définit h, γ et θ respectivement comme la hauteur du fluide, la tension superficielle du fluide et l'angle de contact entre le fluide et la surface du tube. Aussi ρ la masse volumique du fluide, r le rayon du tube et g l'intensité de la pesanteur. Le rayon du tube doit être sufisamment petit devant la longueur capillaire pour qu'il y ait ascension.

(Voir onglet "Nos expériences" sur l'ascension capillaire dans une fleur).