Helium 4

Propriétés de l'hélium superfluide :

L’hélium est un élément chimique aux propriétés spectaculaires, mais pour pouvoir sans rendre compte, il faut se trouver dans des situations tout à fait particulières, ou du moins inhabituelles. Pour observer sont caractère unique, il faut se trouver en dessous de 2,17K (à ne pas confondre avec les 2,17°C). A de si basse températures les systèmes que l’on étudient sont placés dans des cryostats, sorte de congélateurs super puissant qui permettent de créer et d’entretenir ces températures extrêmement faibles. Pour que cela soit possible, il est nécessaire que le système soit parfaitement (ou presque) isolé de l’extérieur, et donc que le cryostat sépare l’hélium de l’extérieur par du vide .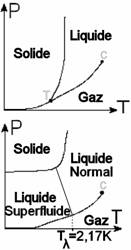

Une fois dans ces conditions extrêmes, qu’observe-t-on ? Un liquide superfluide !

Un liquide à cette température ! Oui car l’hélium est un liquide permanent (voir le diagramme de phase comparatif ci contre entre un élément quelconque et celui de l’hélium) mais aussi superfluide, c’est à dire en autre qu’il ne possède pas de viscosité (du moins apparente).

Ces propriétés sont uniques, et elles sont spécifiques à l’hélium ( 4He ou son isotope 3He). Elles s’expliquent par les caractéristiques de l’hélium qui sont : sa faible masse et son caractère de gaz rare.

Regardons plus en détail ce qu’est la superfluidité. Il s’agit d’une sorte de nouvel état de la matière (comme l’état solide ou gazeux) dérivé de l’état liquide. C’est un liquide spécial qui a la propriété d’être «parfait » au sens de l’hydrodynamique : il est non visqueux.  En réalité ce n’est pas totalement exacts, et la perte de viscosité est en réalité progressive. Pour expliquer cela, on a introduit le modèle à deux fluides qui séparent virtuellement l’hélium superfluide en deux parties. L’une normale et l’autre superfluide parfaite. Cette seconde partie est non visqueuse et à aussi la propriété d’avoir une entropie nulle.

Cette dernière chose conduit alors a un effet étonnant : l’effet thermomécanique.

 

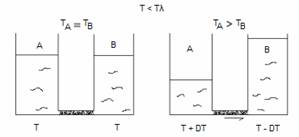
Il s’agit d’une variation de température issue d’un déplacement de matière : le déplacement de la fraction superfluide (voir ci-contre : les deux tubes étant reliés par un fritté afin de bloquer la fraction normale). Lors de son passage d’un tube à l’autre, elle n’apporte pas d’entropie, mais uniquement de la masse. L’entropie massique diminue et donc la température baisse. Inversement dans le tube de départ la température augmente.

Les propriétés étonnantes de ce liquide on des implications tout aussi remarquable. Plusieurs types de sons vont pouvoir exister. Il en existe au total six, mais nous ne nous intéresserons ici qu’aux trois premiers.

Le premier (classique) va correspondre à un déplacement en phase des fractions normale et superfluide, tandis que ce que l’on appelle le deuxième son sera un déplacement en opposition de phase de ces deux fractions, de sorte que la quantité de matière en un point donnée ne change pas.

Le troisième son existera lorsque l’on se placera dans le cadre de l’étude de film mince (quelques couches atomiques ; 1 a.l=3,6 Å). Dans ce cas la fraction normale sera bloquée contre le substrat et seul la fraction superfluide va se déplacer. On comprend tout de suite l’importance que vont jouer les effets d’interfaces entre le fluide et le substrat. La force de Van der Waals va jouer le rôle d’une force de rappel. En effet, après calcul, on trouve que le film est soumis à un potentiel de la forme :

Où q est constitutif du matériau.

On peut donc en déduire que la force de Van der Waals que subit le film est donné par :

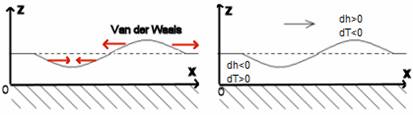
Cette dernière expression est essentielle. Elle représente un des éléments à l’origine du troisième son : la force de Van der Waals joue le rôle d’une force de rappel (voir figure).

 

D’autre part, à cause de l’effet thermomécanique, il s’agit d’une onde de température (on peut rappeler que seule la fraction superfluide à la possibilité de se déplacer), mais aussi d’une onde d’épaisseur puisque l’on peut considérer que le film est incompressible.

Le troisième son est une onde de température et d’épaisseur.

Afin de mesurer ce troisième son, dont la vitesse est donnée par la formule suivante ci dessous,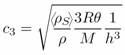

nous allons être amener à utiliser du matériel très spécial, voir même crée sur mesure les capteurs que nous allons utiliser. Pourquoi ? Et bien car il n’est pas simple de mesurer des variations de températures de l’ordre de quelques centaines de mK jusqu’à quelques dizaines de µK, et que c’est bien dans ce contexte que nous allons travailler.