Méthode et techniques de recherche
1. Notre démarche
Au premier abord, notre problème pouvait paraître relativement élémentaire étant donné la simplicité des objets mis en jeu: une série de masses reliées par des ressorts.Cependant, il ne faut pas oublier que cela peut en fait correspondre àdeux masses comme à une dizaine voire plus, et dans ce dernier casle nombre de variables et d'équations devient rapidement impressionant.
Alors comment franchir l'étape entre ce système élémentaire à une ou deux masses et celui plus complexe à N masses?
Dans un premier temps nous avons donc décidé d'exploiter à fond nos connaissances sur le système simple: on fait l'analyse et pour faire encore plus simple on sépare d'abord le mouvementvertical (animé par la gravité et le trampoline) du mouvementhorizontal ( dû aux ressorts et aux éventuelles masses encontact entre elles). Un outil très important dans cette analyseest le portrait de phase, c'est-à-dire le tracé de la vitesseen fonction de la position de la masse. Il révéle trèsclairement des informations extrèmement utiles notamment sur la stabilité: par exemple une courbe fermée indique un mouvement périodique et se répétant a l'infini (comme dans le cas d'un oscillateur harmonique par exemple).
Ici on observe le portrait de phase du mouvement vertical pour une masse. La courbe est fermée, le mouvement se répétant périodiquement. La partie circulaire correspond au rebond sur le trampoline et la parabole à la chute libre.
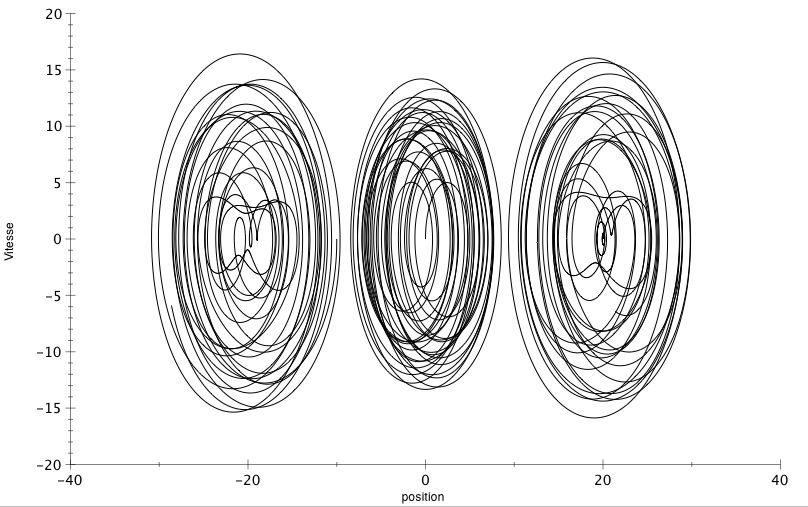
Pour le mouvement horizontal on a tracé le portrait de phase avec 3 masses reliées. Les courbes ne sont pas fermées mais on observe une forme générale de rouleaux, lesportraits de phase des extrémités présentant de fortes ressemblances.
Une fois la modélisation analytique effectuée, on a écrit un programme pour chaque mouvement (ces programmes sont écrits en langage C comme tous les suivants d'ailleurs). Cela permettait à la fois de vérifier nos prévisions analytiques,de faire varier les paramètres pour observer comment réagissait le système et enfin de préparer la suite de la recherche. En effet, en travaillant avec N masses on se doute bien que le nombred'équations à intégrer pour prévoir le mouvementnous obligera à traiter le problème par informatique. On profitedonc de la simplicité du problème à 1 masse (pour lemouvement vertical) ou 3 masses (pour le mouvement horizontal) pour établirle squellette du programme qui nous servira à généraliserpour N masses.
2. Le traitement numérique
Comme expliqué dans la présentation du projet, ce qui nous intéresse particulièrement c'est de connaître la stabilité du système. L'analyse deFloquet est alors pour nous un outil très puissant mais il fautencore être capable de déterminer la matrice de monodromieet ensuite de la diagonaliser. Notre programme principal va donc s'organiserà partir de trois parties: une recréant le mouvement desmasses, la seconde sert alors à écrire la matrice demonodromie, diagonalisée par la troisième partie pour enfinobtenir les valeurs propres.
La fonction d'intégration
A partir de nos programmes décrivant les mouvements verticaux et horizontaux dans les cas simples, on créé une fonctionqui s'occupe de faire l'intégration et d'écrire le mouvementpas à pas pour chaque masse. Il suffit de coupler les mouvements,la partie la plus complexe étant d'écrire les forces àla fois verticales et horizontales que subit chaque masse par les ressorts qui l'entourent, pour une masse occupant une position quelconque dans la chaîne. Il ne faut aussi pas oublier de déterminer les conditions aux limites de la chaîne, c'est-à-dire rendre libres les masses extrêmes aux points correspondants au début ou à la fin de la chaîne. On fait effectuer cette opération pour des conditions intiales différentes: la première correspond au laché de la chaîne a l'horizontale ( situation à portrait de phase fermé) et les suivantes au laché identique mais avec une perturbation sur une des variables. Etant donné qu'il y a 4 variables par masse (deux pour la position et deux pour la vitesse) il y a 4N perturbations possibles.
L'obtention de la matrice de monodromie
C'est la fonction principale du programme. L'analyse de Floquet se réalise sur une période, c'est-à-dire dans notre cas 2Pi. On récupére donc en sortie de la fonction intégration les positions et vitesses des masses au bout d'une période, d'une part pour le mouvement non perturbé et d'autre part pour les mouvements perturbés. On fait alors la comparaison et on aboutit àla matrice de monodromie: chaque ligne correspond à une perturbation d'une des variables et chaque colonne à la différence entre le système perturbé et non-perturbé pour unevariable. La matrice de monodromie et donc une matrice carrée de4N lignes et colonnes.
La diagonalisation
Cette étape nous paraissait la moins importante et s'est révélée tout aussi difficile que les précédentes. Encore une fois c'est le nombre important de masses qui change tout. Diagonaliser une matrice 40 par 40 (par exemple pour dix masses) ne se fait pas aussi simplement qu'une matrice 4x4, même numériquement. Nous avons du utiliser un algorithme (étudié en info au premier semestre...comme quoi c'est utile!) utilisant la méthode de Jacobi. Cependant celui-ci ne permettait de diagonaliser que les matrices sous certaines formes, il a donc fallu l'aménager pour qu'il convienne a des matrices quelconques.
Au final, on obtient les valeurs propres et leur module respectif.Il ne reste plus qu'à déterminer si elle traduise la stabilitéou l'instabilité.
3. L'obtention et le traitement des résultats
Le programme nous renvoie donc N valeurs propres imaginaires dont on prend le module. Pour certaines valeurs de paramètres ils sont tous compris entre 0 et 1, pour d'autres on dépasse la valeur 1: c'est l'instabilité.
On fait tourner le programme en variant un paramètre tout en fixant l'autre un nombre de fois assez importants pour obtenir la loi de stabilité en fonction du paramètre. On peut ainsi prévoir la stabilité de notre chaîne: c'est gagné!
4. L'animation
Pour l'animation on a utilisé la même fonction intégration que pour le programme précédent. Ensuite avec le traceur pgplot on génére des images à lasuite correspondant à chaque pas de l'évolution du mouvement.On visualise alors l'animation et on peut vérifier si les limitesde stabilité sont bien conformes à celles donnéespar le programme précédent, si on est dans des conditions stablesla chaîne ne fait que rebondir à l'horizontal, si on est dansdes conditions instables la chaîne se déforme à partird'un certain moment. Dans les cas instables on pourra parfois noter quelqueseffets pseudo-périodiques mais il est difficile d'interpréter ces mouvements.
