L’effet du facteur de transcription sur le taux de transcription de ses gènes cibles est décrit par une équation non linéaire :
dY/dt = production - dégradation = f(X*) - αY
Considérons en premier le taux de production de la protéine Y contrôlé par le facteur de transcription X. Quand x régule y ce qui est représenté par le réseau x 
y, le nombre de protéines Y produit par unité de temps, est une fonction de la concentration de X dans sa forme active, X*.
d’où Taux de production de Y = f(X*)
Typiquement, la fonction de régulation f(X*), est une fonction monotone, « en forme de S » appelée fonction de Hill (cf. Figs. Ci-dessous). C ‘est une fonction croissante quand X est activateur (g1) et décroissante quand X est répresseur (g2). La fonction de Hill est une fonction utile qui décrit la régulation de beaucoup de gènes.
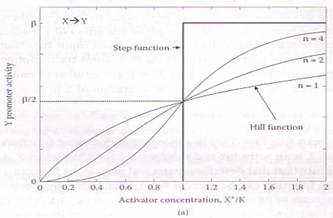
Pour un activateur, la fonction Input de Hill est une courbe qui, partant de 0 croît pour atteindre un niveau maximal (de saturation). Elle est décrite par :
f(X*) = β / [1+(Kx/X*) n]
On peut approximer cette équation (lorsque n -> ∞) par la fonction step (de Heavyside):
f(X*) = β θ(X* > K) (g1) (Reproduction de la figure 2.4 p.14 du livre d’ALON) :
Fonction de Hill pour un répresseur est une fonction qui partant d’un maximal décroît :
f(X*) = β / [1+(X*/Kx) n]
pour n -> ∞ f(X*) = β θ(X*<K) (g2) (Reproduction de la figure 2.4 p.14 du livre d’ALON) :
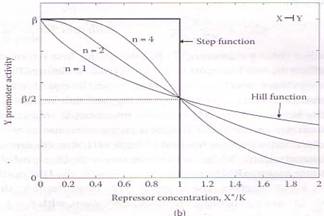
Comme nous pouvons le remarquer la fonction de Hill possède trois paramètres K, β et n. Le premier paramètre K correspond au seuil d’activation. Il définit la concentration de X* nécessaire pour activer de manière significative l’expression du gène. A partir de l’équation il est facile de voir qu’il existe un point d’inflexion lorsque X* = K, et en s’intéressant à la fonction step nous remarquons que K représente bien le seuil à partir duquel X change de valeur. (La valeur de K est liée, entre autre, à l’affinité chimique entre X et son site sur le promoteur du gène y.) Le second paramètre de la fonction de régulation est le niveau maximum d’expression du promoteur, β, c'est-à-dire que β représente le taux de production maximal pouvant être atteint par le gène y. Ce taux tend à être atteint pour de hautes concentration de l’activateur c'est-à-dire lorsqu’ X* >> K. En effet cela traduit le fait que pour de grandes concentrations, X* fixe le promoteur avec une probabilité plus élevée, on a donc une stimulation de l’ARNp entraînant alors la production de beaucoup d’ARNm par unité de temps. Pour finir, n sert à définir la raideur de la pente de la fonction de Hill, plus n est grand plus la fonction de Hill tend vers une fonction step (Heavyside), n variant généralement de 1 à 4.
Dans un réseau de régulation tel que celui de la Fig. 2.3, chaque lien est caractérisé par une fonction de Hill. En fait, on peut estimer que ce lien est soumis à la sélection naturelle, autrement dit, un lien peu utile, deviendra facilement cible de mutations, et disparaîtra.
La variation de concentration de Y (dY/dt) décrite par une équation de dynamique est due à la différence (avec α : coefficient de dégradation/dilution) :
dY/dt = β - αY
A l’état stationnaire, Y atteint une concentration Y st. L’état stationnaire de concentration s’obtient en résolvant l’équation dY/dt = 0, ce qui nous donne :
Yst = β / α
Qu’arrive t’il maintenant si le signal Sx cesse (d’où β = 0) ?
La solution est de la forme d’une exponentielle décroissante de la concentration Y :
Y (t) = Yst 
On peut définir un temps caractéristique pour la décroissance de Y. Une mesure de la vitesse à laquelle Y varie est donnée par le temps de réponse T(1/2), défini comme le temps qu’il faut pour atteindre une diminution de la concentration de Y par un facteur 2. Il est ainsi obtenu en résolvant l’équation Y (t) = Yst pour Y (t) = Yst / 2.
T(1/2) = log (2)/ α
Notons que α détermine directement T(1/2). En effet il permet des variations rapides de la concentration. Le taux de production, β, quant à lui affecte l’état stationnaire.
Nous avons vu que la perte de signal d’entrée provoquait une décroissance exponentielle de Y. Considérons maintenant le cas où nous partons d’une cellule non stimulé (Sx = Y = 0) à laquelle nous fournissons brusquement un signal important Sx afin que la protéine Y commence à s’accumuler. La solution de l’équation de la dynamique vue précédemment devient alors :
Y (t) = Yst (1 - )
La concentration de Y croît en partant de 0 et converge graduellement vers l’état stationnaire Yst = β / α.
Remarquons qu’aux temps initiaux (t << 1), d’après l’approximation de Taylor ( on utilise ~ 1 – αt et Yst = β / α ), nous avons Y ~ βt.
Nous trouvons de même T1/2 = log (2)/ α.
Ainsi nous venons de voir que le temps de réponse en ce qui concerne la décroissance et la croissance reste identique, il est seulement gouverné par le taux de dégradation/dilution, α (plus α est grand, plus le changement dans la concentration de la protéine est rapide).