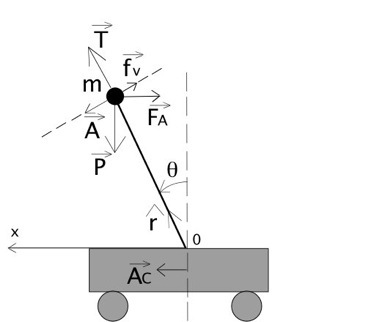
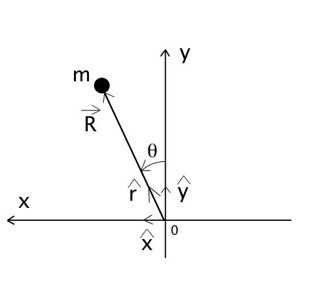
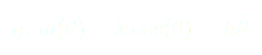SCHÉMA D’UN PENDULE FORCÉ INVERSÉ :
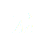
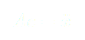
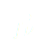
avec le chariot et est subie par le pendule.
On étudie le pendule dans le référentiel du chariot qui est un référentiel en translation accéléré par
. Il en découle alors une force fictive
subie par le pendule dans ce référentiel et définie par :
Comme précédemment pour le pendule simple inversé, on applique la seconde loi de Newton en considérant le pendule comme système :
Comme notre projet consiste à éviter la chute du pendule nous allons nous intéresser seulement aux angles proches de la position d’équilibre instable (cf. pendule simple inversé), c’est à dire seulement aux petits angles. On pourra donc faire des simplifications à l’aide de développements limités.
De plus (pour le moment) on négligera la force de frottements visqueux.
QUELQUES REMARQUES AVANT DE COMMENCER :
ÉQUATIONS DU MOUVEMENT :
Somme des forces :
On fait alors le produit vectoriel de
avec chacun des membres :
avec 
la masse du pendule.
La longueur du pendule, elle, est égale à
.
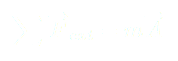
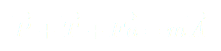
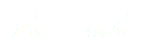
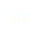
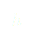
(1)
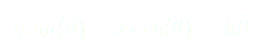
Euler-Lagrange :
Cette méthode est la plus évidente mais n’est pas la plus rapide ni la plus propre.
C’est pourquoi nous proposons une seconde méthode qui est celle d’Euler-Lagrange.
Dans un premier temps, il faut écrire le vecteur position du pendule
:
(2)
On dérive alors cette expression pour obtenir la vitesse du pendule
:
(3)
Le Lagrangien 
s’écrit par définition :
On a déjà décrit l’énergie potentielle du pendule par l’équation (1) du pendule simple inversé. L’énergie cinétique est définie par :
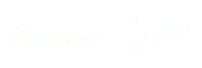
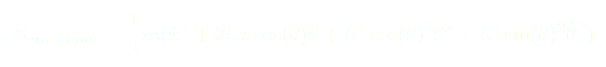
ADIMENSIONALISATION :
Comme nous l’avons fait précédemment pour le pendule simple inversé, nous allons remplacer notre variable 
par une nouvelle variable 
avec 
une nouvelle unité de temps définie comme par
et 
.
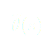
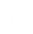
Après ce premier changement de variables on obtient :
On effectue un deuxième changement de variables en posant 
.
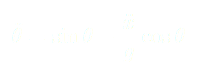
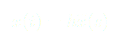
On dérive une première fois par rapport au temps :
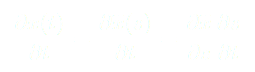
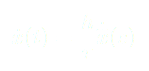
On dérive une seconde fois par rapport au temps et on trouve :
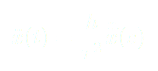
Finalement on obtient une équation sans dimension :
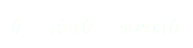
(9)
On connaît donc une équation du mouvement d’un pendule inversé forcé. On veut maintenant pouvoir tracer son portrait de phase autour de sa position d’équilibre instable pour le stabiliser. On passe donc à une nouvelle partie traitant de la stabilité du pendule forcé inversé.
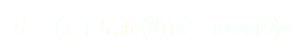
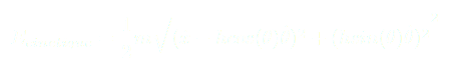
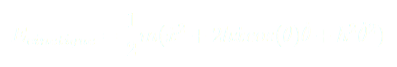
(4)
D’où le Lagrangien :
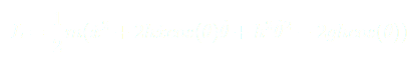
(5)
On utilise alors l’équation d’Euler-Lagrange qui nous permet d’écrire :
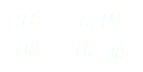
(6)
Après calculs de chacun des termes on trouve :
On retrouve bien le résultat précédent :
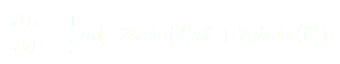
(8)
(7)
