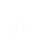
D’après les conditions posées ci dessus, on cherche une fonction bien définie en 0 de la forme :

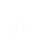
D’après les conditions posées ci dessus, on cherche une fonction bien définie en 0 de la forme :
SYSTÈME IDÉAL :
INTRODUCTION :
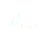
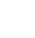

Pour que cette fonction décrive bien notre problème, on pose plusieurs conditions :
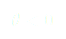
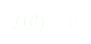
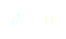
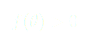
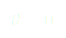
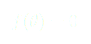
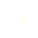
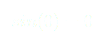
(1)
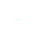
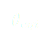
On injecte alors (1) dans l’équation du mouvement adimensionalisée trouvée dans la partie principe du pendule forcé inversé (équation (9)) :
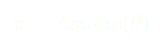
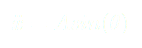
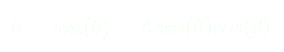
(2)
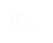
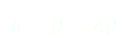
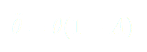
(3)
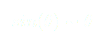
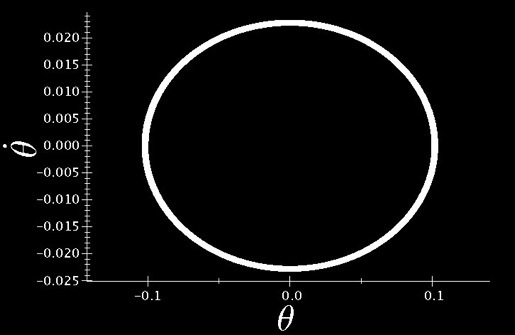
Il ne nous reste qu’à intégrer cette équation par rapport au temps pour obtenir l’équation du portrait de phase. On la réécrit d’abord sous la forme :
Puis on intègre :
On approfondit cette étude du système idéal en s’intéressant au déplacement du chariot, c’est à dire à sa position en fonction du temps.
En utilisant les développements limités on écrit :
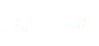
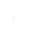
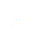
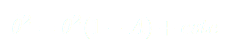

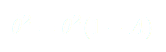
(4)
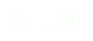
et d’après l’équation (3) :
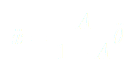
(6)
On intègre une première fois par rapport au temps :
On vient de trouver des équations simples pour résoudre notre système, or on se rend bien compte qu’elles ne peuvent pas décrire un comportement réel.
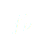
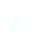
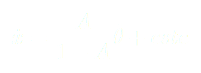
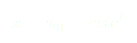
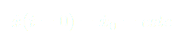
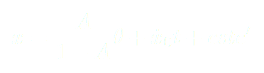
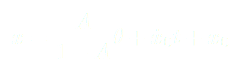
(5)
(7)
SYSTÈME RÉEL :
Le chariot ne peut se déplacer qu’entre deux positions, au delà le pendule est irrattrapable. Pour contrer ce problème on ajoute un terme qui crée une force de rappel.
De façon concrète, tout se passe comme si nous avions un ressort dont la force de rappel serait supérieure à son accélération quand ce dernier approche des valeurs limites. L’équation la plus adaptée à notre système s’écrit donc :
(8)
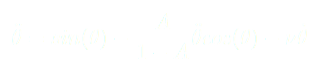
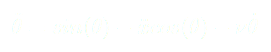
On utilise les développements limités :
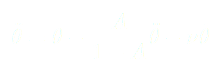
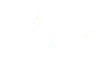
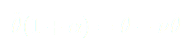
(9)
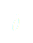
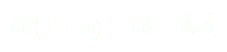
Et on intègre :
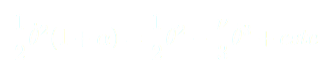

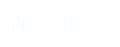
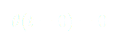
(10)
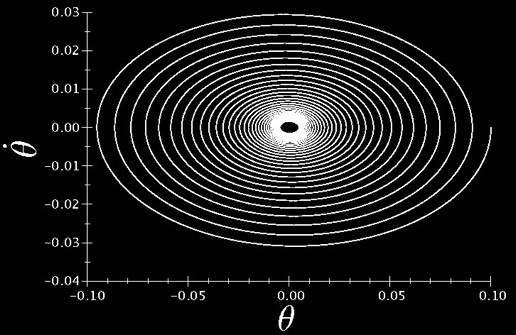
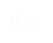
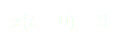
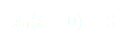
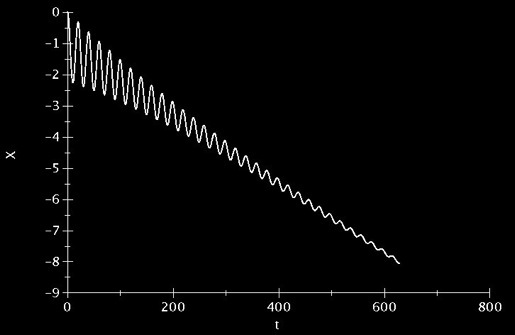
Tout se passe comme si notre système et qu’il se déplaçait à vitesse constante ce qui implique que le chariot aura tendance à aller vers l’infini. Or lorsque l’on va appliquer ce résultat aux moyens disponibles pour la réalisation (table traçante), on ne peut pas l’utiliser. En effet, nous sommes limités, la table traçante ne mesurant qu’une vingtaine de centimètres.
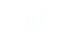
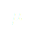
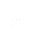
(11)
En introduisant ce résultat dans l’équation (8) on a :

MODÈLE APPLICABLE À LA TABLE TRAÇANTE :
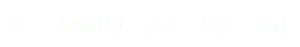
(13)
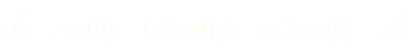
Pour les petits angles :
(12)
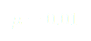
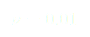
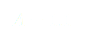
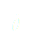
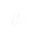
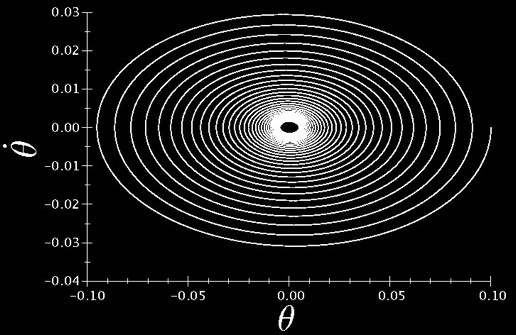
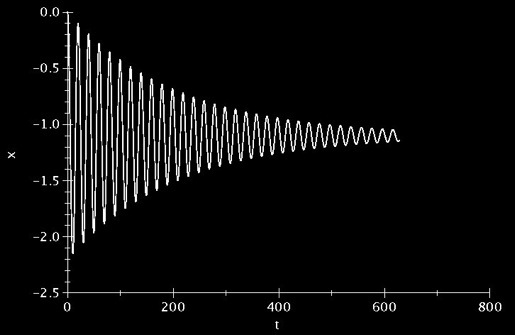
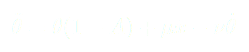
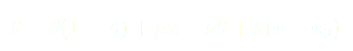
(14)
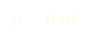
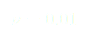
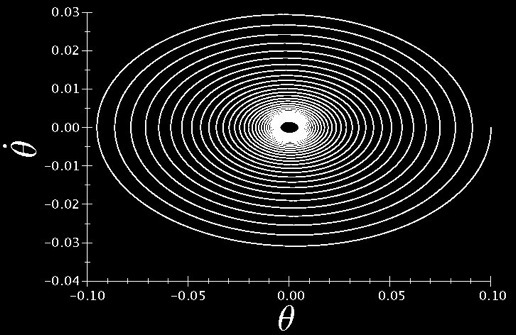
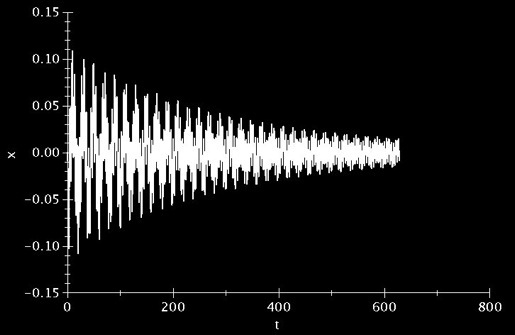
Nous avons donc trouver un forçage qui nous permet de stabiliser le pendule sur son équilibre instable tout en respectant les contraintes de l’expérience.
Maintenant nous allons résoudre de manière analytique en utilisant une méthode perturbatrice.