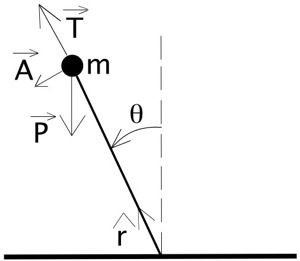
SCHÉMA D’UN PENDULE SIMPLE INVERSÉ :


ÉTUDE DES POINTS D’ÉQUILIBRE :
Ce schéma représente un pendule simple inversé, c’est à dire une barre rigide fixée à un socle à son extrémité inférieure et possédant une masse liée à son extrémité supérieure.
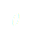
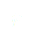
Pour déterminer les points d’équilibre d’un pendule simple inversé (ou d’un pendule simple, le raisonnement étant le même) il faut écrire l’énergie potentielle du système qui est :
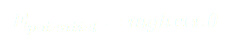


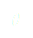
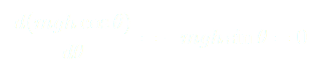
(1)
(2)
On regarde alors le signe de cette dérivée seconde pour chacune des solutions. Si le signe est positif, le point d’équilibre est stable, et s’il est négatif, le point d’équilibre est instable. On trouve :
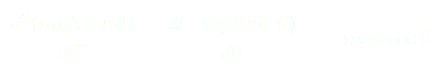
(3)


et
En mécanique, l’étude du mouvement d’un système débute généralement par l’application de la seconde loi de Newton. Cette loi vérifie l’égalité :
PORTRAIT DE PHASE :
Pour comprendre la dynamique d'un système il suffit tout simplement d'étudier son portrait de phase.
Un portrait de phase est un graphique représentant la vitesse en fonction de la position, il faut donc trouver une équation de la forme :
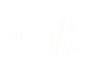
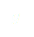

On peut donc réécrire l’équation (6) :
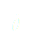
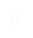
Somme des forces :

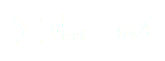

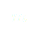
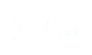

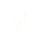
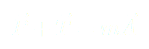
(4)
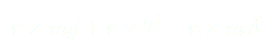
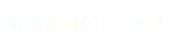
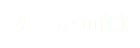

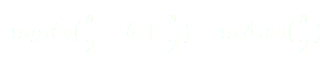

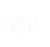
Finalement, une équation du mouvement est :
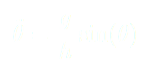
(5)
(6)
Adimensionalisation :
On va simplifier l’étude de cette équation en la réécrivant sans dimension.
(7)
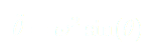


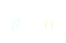

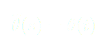
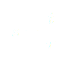
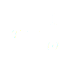

On dérive une première fois par rapport au temps :
On dérive une seconde fois par rapport au temps :
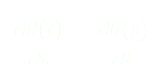

(8)

On injecte ces résultats dans l’équation (7) :
(9)
(10)
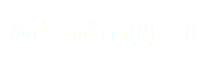

(11)
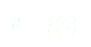
Or à notre niveau, on ne sait pas intégrer (11) par rapport au temps.

(12)
Equation du portrait de phase :

D’où, (11) devient :
(13)
Maintenant, on sait intégrer une telle fonction en fonction du temps en écrivant (13) sous la forme :
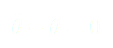
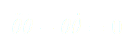
Dont la primitive est :
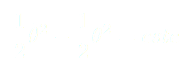
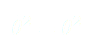
(14)

Portrait de phase pour des petits angles :



Maintenant que nous connaissons la dynamique du pendule simple inversé nous pouvons passer à l’étude du principe du pendule forcé inversé.
