INTRODUCTION :
Jusqu’ici nous nous sommes limités à la résolution numérique pour expliquer nos hypothèses et nos observations.
Dans cette section nous allons résoudre analytiquement les équations du mouvement de notre système à l’aide de la théorie des perturbations.
ÉQUATIONS :
Nous avons deux équations différentielles couplées. Nous allons faire apparaître un coefficient réel que l’on notera 
avec comme condition 
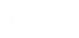et que l’on mettra en facteur avec les termes en 
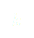et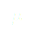 
pour faciliter la résolution des équations.
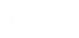
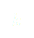
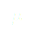
Ceci revient à supposer que les forces fictives de friction et de rappel sont faibles par rapport à 
. Nous prendrons par souci de simplicité les équations adimensionalisées qui sont les suivantes :
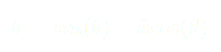
(1)
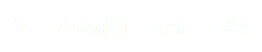
(2)
En utilisant les développements limités au premier ordre et en introduisant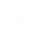 
dans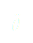 
on a :
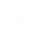
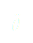
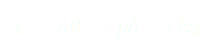
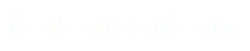
(4)
(3)
Nous savons que pour ce genre d’équations, nous avons des solutions de la forme :
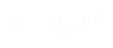
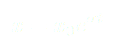
avec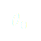 
la position initiale du pendule et 
celle du chariot.
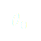
Les équations (3) et (4) deviennent :
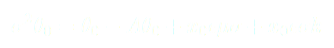
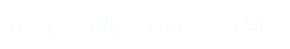
A partir de (6) on peut écrire que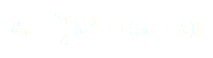 
il vient alors :
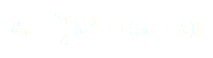
(5)
(6)
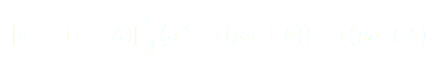
(7)
Quand nous résolvons cette équation pour 
à l'ordre zéro, il vient alors deux solutions :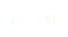 
et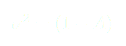
.
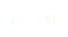
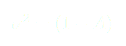
Si nous ré-injectons ces solutions dans l'équation (7) nous observons qu'elle n'est pas vérifiée. Nous allons donc chercher le terme correctif qui pourrait donner une meilleure approximation de la solution. Remarquons d'abord qu'il est de l'ordre de 
. Nous allons donc poser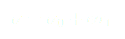 
, 
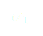est l'erreur recherchée. Pour la trouver, il faut résoudre l'équation (7) pour 
à l'ordre 1.
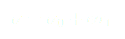
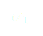
Avec ce nouveau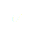 
l'équation (7) devient :
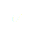
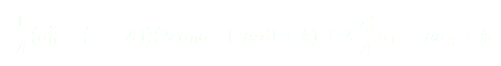
(8)
Si nous résolvons l'équation (8) il vient alors pour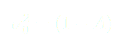
:
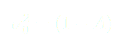
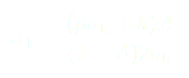
Maintenant remplaçons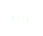 
par sa valeur, à savoir dans notre cas pour 
:
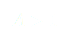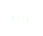
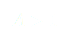
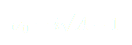
Posons aussi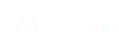
. Il vient :
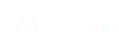
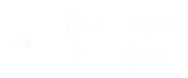
En prenant la partie réelle de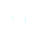 
:
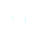
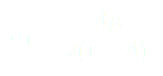
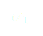
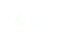
Rappelons que nous recherchons une solution stable pour l'angle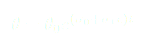 
. Il faut donc que 
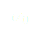et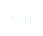 
soient négatifs donc que 
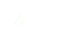pour que 
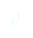tende vers zéro.
Maintenant que la théorie est bien comprise, nous pouvons passer a la partie expérimentale de notre projet.