Diffusion du photon

Diffusion d'un photon.

Introduction :

Les expériences étudiées consistent à mesurer à analyser les propriétés de transmission de la lumiére de différents échantillons .
C'est pourquoi il nous a été nécéssaire de revenir sur les différents phénoménes de diffusion qu'il est possible d'observer .
Dans cette partie , nous avons tenté de demontrer certaines lois de diffusions le plus simplement possible .

Loi de diffusion et loi de Beer – Lambert :

La loi de Beer-Lambert est très utilisée , notamment dans le domaine de la chimie .
On peut aisément la comprendre en considérant un échantillon traversé par un faisceau lumineux d'intensité Io dont on mesure l'intensité en sortie I.

Soit dI la perte d'intensité , admettons que celle-ci soit proportionnelle à :

dx : element de longueur dans la direction de propagation de l'onde

ῥ : densité volumique d'espèce en question

I : intensité incidente

Ainsi , nous pouvons poser :

dI=- a.ῥ.I.dx .

Où a représente le coefficient d'absorption , caractéristique du matériau étudié.

D'où :

(dI / I)=- a.ῥ.dx

En intégrant on obtient directement :

I=Io.exp(-a.ῥ.x)

plus connue sous le nom de Loi de Beer – Lambert .

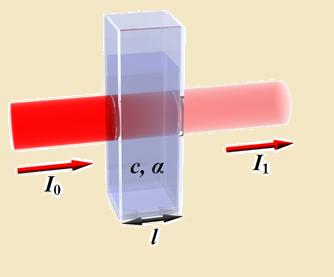
A noter que dans ce cas ,on ne prend en compte que les photons qui n'ont jamais été diffusé,c'est à dire ceux qui ont traversé l'échantillon sans rencontrer un seul élément diffusant.

Comme montré sur le schéma ci-dessus , cette loi ne prend en considération que les photons
qui n'ont jamais été diffusé , correspondant au trajet bleu .
On ne tient pas compte des photons qui peuvent subir plusieurs diffusions et , eventuellement ,
revenir sur le détécteur (trajet rouge) .
Il est donc evident que cette

2. Transmission dans un système à une et deux dimensions :

Afin de bien comprendre le problème,nous avons décidé de le traiter le plus simplement possible .
Nous raisonnerons en terme de probabilités :

Considérons un photon soumis à une marche aléatoire isotrope , qui a donc la même probabilité de se diriger dans toutes les directions .

Cas à 1Dimension :

Soit une bille sur un rail de n cases , pouvant se déplacer ou à droite ou à gauche . On pose d le nombre de sauts effectués à droite et g ceux effectués à gauche . La bille a une probabilité identique de faire un saut à droite ou à gauche . Celle-ci est donc égale à ½ .

Dans notre cas simpliste , le bille représente le photon traversant le milieu diffusant , tandis que les cases représentent les elements diffusant du milieu .

Si on appelle N le nombre de sauts totaux effectués par la bille , on a :

N=d+g

Or g=d-n , on obtient directement d en fonction de N et n:

d=(N+n)/2

On sait que la probabilité de trouver la bille à la x-iéme case après N sauts obéit à la loi binomiale :

P(x=n)=(1/2)^N . (N!/((N-n)!.n!))

A l'aide de l'approximation de Stirling , on trouve :

ln(P)=(-x²/N)-N.ln(2) .

P(x=n)=exp(-n²/N -N.ln(2))=(exp(-n²/N))/(2^N) .

Ce résultat représente la probabilité que la bille se trouve dans la case n aprés N sauts .
En aucun cas il ne s'agit ici de la probabilité de sortie du photon.
Pour obtenir celle-ci , il faudrait integrer notre résultat pour x variant de n à l'infini .
Nous obtiendrons ainsi la probabilité que le photon se trouve dans n'importe quelle case se trouvant entre n et l'infini (dans notre cas : le détécteur) .

Revenons à présent au cas du photon;
si N est le nombre de sauts totaux
l* le libre parcours moyen de celui-ci,on a:

N=(c.t)/l*

Où c est la vitesse du photon dans le milieu et t le temps .

Or ,

n =L/l*

avec L la longueur de notre échantillon .

N représente donc le paramètre temps,n le paramètre longeur L.

Nous retrouvons ainsi une dépendance en :

exp(-L²/(l*.c.t))

A noter que lorsque l'on fait tendre N vers l'infini,la probabilité de sortie du photon tend à s'annuler , ce qui revient à dire que le photon se retrouve comme piégé à l'intérieur du système : cet état est dit localisé . A une dimension , l'état est toujours localisé .

Cependant , le cas à une dimension ne refléte pas de phénoméne physique réalisable .
Mais son explication facilite la comprehension lorsque l'on passe à 2 ou 3 dimensions .

Cas à 2Dimensions :

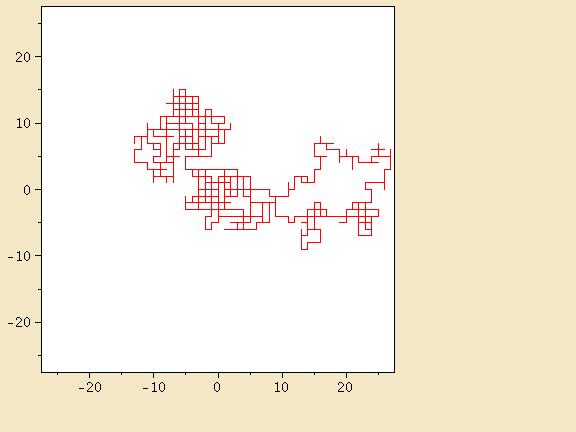
Le problème reste relativement identique au précédent sauf qu'il est nécessaire d'ajouter 2 nouveaux degrés de liberté .

Nous estimons que l'épaisseur de l'échantillon est très grande devant sa longueur,autrement dit nous pouvons supposer que sa taille est infinie selon la direction y.

Appelons h le nombre de sauts en haut et b le nombre de sauts en bas . On a alors , si N est le nombre de sauts totaux , N=d+g+h+b.

Il convient de poser x=d-g et y=h-b .

On a alors , en posant g=d-x , N = 2.d-x+h+b .

D'où d= (N+x)/2 – (h+b)/2

Afin de faciliter le calcul,il convient de poser 2 hypothèses :

on admettra x=d-g très petit devant N .

nous prendrons (h+b)/2 = N/4 , en considérant qu'il y a autant de chance que le photon fasse un saut à droite , à gauche , en bas ou à droite .

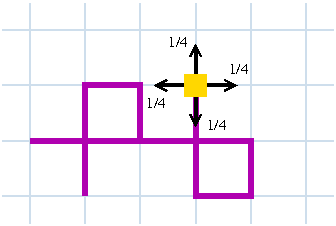
Aprés calcul et approximations, nous trouvons le résultat suivant:

P(x=n)=exp(-0,13.N +0,45.n – n²/N)

De la même façon que dans le cas à 1D , pour obtenir la probabilité Pt de sortie (ou de transmission du photon) , il faudra faire :

Comme précédemment on peut relier N au temps et n à la longueur L de l'échantillon . En effet N=c.t/l* et n=L/l* . A noter que n est la valeur maximale atteinte par x .

Ce modèle ne prend pas en compte la dimension finie du système . Autrement dit , une fois que les photons sont sortis de l'échantillon , ils peuvent revenir à l'intérieur .

Intéressons nous de plus prés au terme dominant en -n²/N qui peut être remis sous la forme -L²/(l*.c.t) . On peut ainsi identifier un temps caractéristique ζ=L²/l*.c .

Extrapolation à des milieux finis :

Dans un milieu fini , on s'attendrait , d'après Maret à obtenir une dépendance dans l'exponentielle en -t/L² .

Avec nos connaissances en probabilité , nous n'avons pas réussit à modéliser un système fini . Autrement dit , nous avons calculé une probabilité que la bille soit dans une case donnée (dans la n-iéme case) au bout d'un temps donné (N sauts) sans tenir compte que celle-ci à pu dépasser la n-iéme case puis revenir .

Ce phénomène n'est pas physiquement satisfaisant , c'est pourquoi il est important d'intégrer notre probabilité pour x allant de n a l'infini . Ainsi nous aurons la probabilité que la bille ait dépassée la valeur extrême n (L pour le photon) de l'échantillon . Celle-ci ne pourra plus subir aucune diffusion .

Cette probabilité est en rapport direct avec le coefficient de Transmission qui nous intéresse . Il suffira d'intégrer sur tout les temps .

retour a l'accueil