Lorsqu'une onde se
propage dans un milieu comportant des impuretés, celle-ci est soumise au
phénomène de la diffusion.
Si l'on observe ce phénomène a travers un
échantillon de matière comme l'ont fait Lagendijk et Maret, on
s'apperçoit que l'intensité de l'onde en sortie de l'échantillon varie
en fonction de l'angle.
On remarque ainsi que la direction privilégié, est la direction incidente.
De plus pour de très faible angles autours de la direction incidente, l'intensité forme un pic que l'on appel localisation faible.

Pour comprendre d'où vient cette courbe, il est nécessaire de reprendre le concept des interféromètres.
Rappel sur les interféromètres.
Dans
un premier temps nous nous sommes intéressés à un système simple:
interféromètre avec deux chemins optiques différents (Mach-Zender,
Michelson, trous d'Young).
Ensuite, nous avons essayé de généraliser nos observations à un système plus compliqué avec, en théorie, une infinité d'interféromètres superposés.
On représente la lumière qui
arrive sur l'interféromètre par le champ électrique E tel que:
| E = E° . exp(k.r-w.t) . ε |
où ε
représente le vecteur polarisation
k est le vecteur d'onde
w est la pulsation
et :
| I=||E . E*|| |
On décompose le produit scalaire selon la direction du vecteur d'onde. Celle-ci change après toute réflection ou transmission .Le phénomène d'interférence est dû au déphasage qui est introduit par la différence de chemin optique entre deux ondes :
d=d1-d2
Ce phénomène d'interférence se traduit par la mise en évidence d'un terme en cos² dans l'expression de l'intensité.
Par exemple : pour le Michelson
| I(d) ~ cos²(2.k.d) |
2. Rapprochement
avec notre système.
Dans notre étude de la localisation, notre échantillon peut être modélisé par des billes en suspension dans un fluide, comme montré ci-aprés :
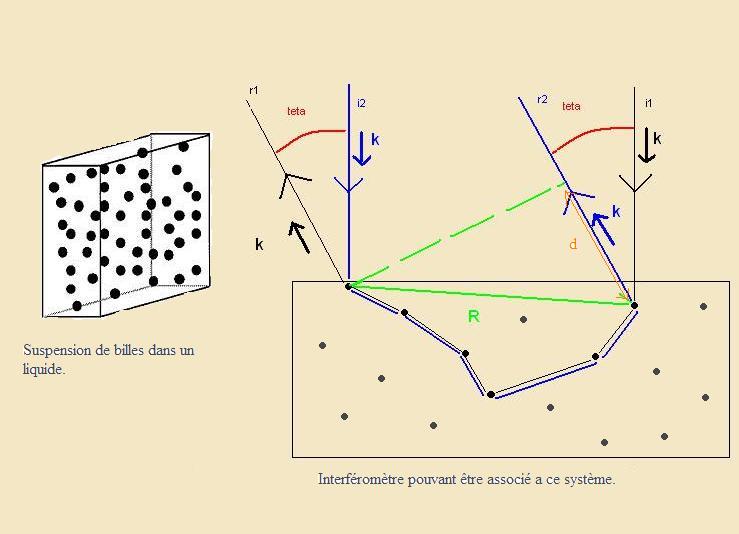
Entre
deux chemins optiques réciproque L1 (bleu) et L1' (noir) , il existe
une différence de chemin
optique d qui traduit donc une interférence.
Ces deux chemins optiques réciproques se comportent comme un interféromètre, or dans un échantillon, toute paire de particules peut constituer un interféromètre.
Au final, notre système se comporte comme une multitude d'interféromètres superposés.
| Itot = I1 + I2 + I3 + ... + Ii + ... + In |
où Ii=||Ei . Ei*||
Il en résulte donc que I est une somme de cos² avec des arguments différents, dépendant chacun de la distance inter-particules Ri et de l'angle d'observation. Tout ces cos² étant centré en zéro, ceci explique le cône observé dans la direction incidente (localisation faible).
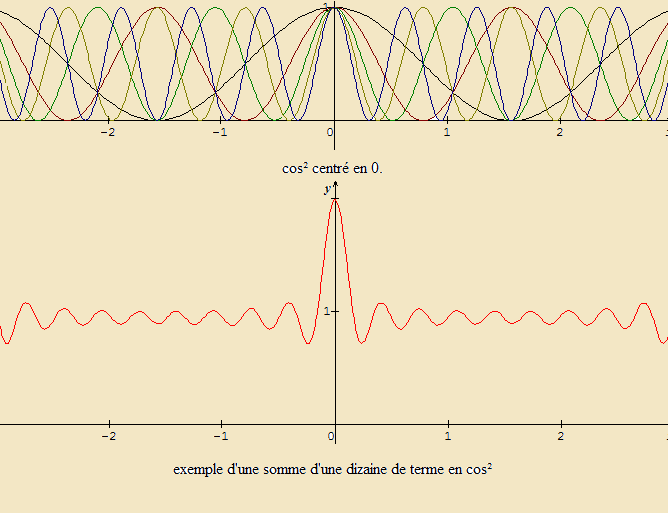
A travers cette exemple, on voit que meme pour un faible nombre d'interféromètre, la localisation faible est observable.
Conclusion: détermination du libre parcours moyen.
Le libre parcours moyen l* correspond à la distance moyenne parcourus par une particule (ici un photon) entre deux choc (ou entre deux diffusion).
La partie calculatoire étant lourde, nous admettrons directement que l'angle α que fait la pointe de la localisation faible est proportionnel à 1/l*.
on a α~λ/1,3.l*
|
α~1,3.π/k.l* |
Ce qui fait apparaître k.l*
dans le cadre de la localisation d'Anderson, le produit k.l* est important, il s'agit du critère de Ioffe-Regel: pour observer le phénomène de localisation, il faut que ce produit soit se l'ordre de 1.
Cette mesure du critère de Ioffe-Regel est une étape obligatoire pour savoir si oui ou non, on pourra observer une localisation dans notre échantillon.
Lagendijk
réussit dans ses expériences à obtenir des échantillons dont le
produit k.l* varie de 1,5 à 76. Pour Maret, ce produit est compris
entre 2,5 et 6,3.