 Le Phoenix de l'Electromagnétisme : l'Effet Maxwell-Lodge
Le Phoenix de l'Electromagnétisme : l'Effet Maxwell-Lodge
 Le Phoenix de l'Electromagnétisme : l'Effet Maxwell-Lodge
Le Phoenix de l'Electromagnétisme : l'Effet Maxwell-Lodge

Université de Nice
| Elèves : | Andréï Belokogne et Ivan Belokogne (L3 Physique) |
| Encadrants : |
Germain Rousseaux : Germain.ROUSSEAUX@unice.fr Richard Kofman : Richard.KOFMAN@unice.fr |
 |
 |
| Yakir Aharonov | David Bohm |
L'effet Aharonov-Bohm [1] décrit comment un champ magnétique B se trouvant dans une région de l'espace inaccessible à une particule chargée, influe sur l'état quantique de celle-ci. En premier cet effet a été découvert par Ehrenberg et Siday. Puis, indépendamment, en 1959 Aharonov et Bohm ont fait une étude théorique approfondie montrant un fort lien avec les applications fondamentales de la mécanique quantique. Ce travail a attiré l'attention sur le rôle important des potentiels électromagnétiques dans la théorie quantique.
L'existence de l'effet est expliquée par la présence des potentiels électromagnétiques dans l'équation de Schrödinger. Le potentiel vecteur définit la phase de la fonction d'onde, or la géométrie multiplement connexe* conduit à l'observation d'un effet d'interférences en l’absence de l'action directe d'un champ électromagnétique sur la particule. L’expérience d’interférences avec les trous d’Young avec un solénoïde entre les deux trous met en évidence cet effet par le déphasage des franges dans la figure d’interférence qui est proportionnel à la circulation du potentiel vecteur externe au solénoïde.
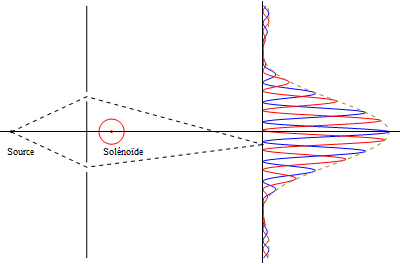
En prenant comme source les électrons, on observe le déphasage en terme de la densité de probabilité (cf. www.physics.brocku.ca) :
sans le flux magnétique :
déphasage de 3π :
Comme l'espace est doublement connexe*, on peut représenter le solénoïde par un arbre et la dénsité de probabilité par les skis :

* L’espace multiplement connexe est un espace où il existe au moins une boucle fermée ne pouvant pas être réduite à un point.
* L’espace doublement connexe est un espace multiplement connexe avec un seul trou.
 |
 |
| James Clerk Maxwell | Oliver Lodge |
L'effet Maxwell-Lodge montre que si l’on fait passer un courant alternatif à travers un solénoïde parfait et si l’on mesure la tension au bornes d’une spire entourant ce solénoïde, on observe qu'elle n'est pas nulle. Or, on sait qu’il n'y a pas de champ magnétique à l'extérieur d'un solénoïde parfait. Dans le cas d’un solénoïde réel, il a été montré que les fuites du champ magnétique ne peuvent pas expliquer cet effet [2]. De plus, on n’observe pas de phénomène de propagation car on se trouve dans le régime quasi stationnaire. (cf. théorie, Champ magnétique et Potentiel vecteur créés par un Solénoïde, On an Electrostatic Field produced by varying Magnetic , Champ électrostatique produit par une induction magnétique variable)
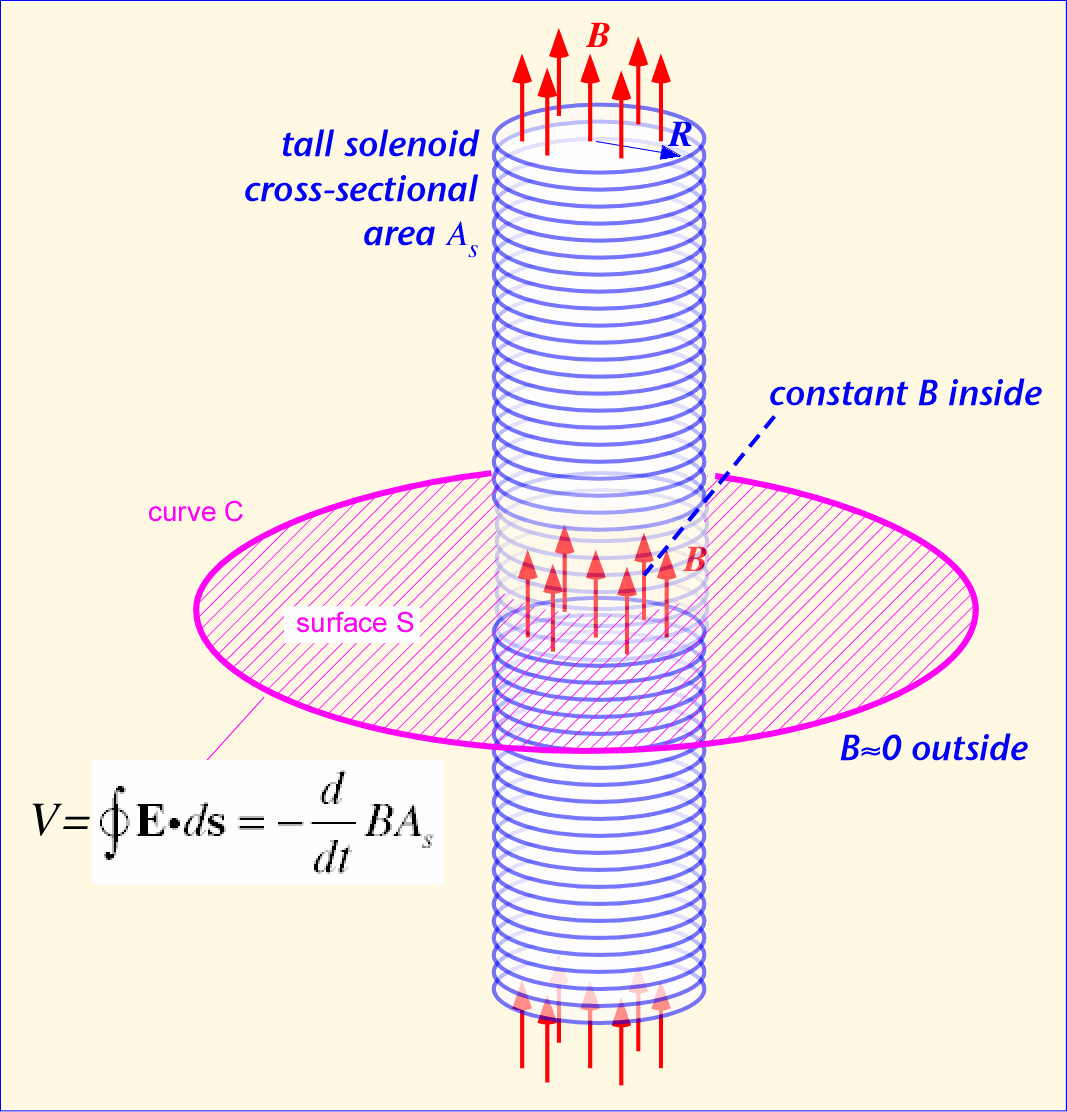 |
 |
Dans cet effet et celui d’Aharonov-Bohm, on a la même géométrie qui est multiplement connexe.
Les travaux suivants ont été réalisés sur le plan théorique et expérimental avant notre projet tutoré : les arguments en faveur de la formulation de l’électromagnétisme en fonction des potentiels (équations de Riemann-Lorenz), l’analogie entre la mécanique des fluides et l’électromagnétisme (correspondance solénoïde-tourbillon), la modélisation d’un solénoïde de taille finie et les fuites du champ magnétique dans le cas du solénoïde réel. [2,3,4,5]
Ici, on va approfondir l’étude de cet effet. Plus exactement, pour écarter les différentes causes possibles de son apparition, autres que le potentiel vecteur, on va utiliser deux types de blindages :
Cependant, si l’on entoure le solénoïde par un blindage qui est fermé, on observe qu’il y a apparition de courants induits dans ce blindage (effet Maxwell-Lodge dans le blindage). Donc, on va étudier cet effet de blindage fermé sur la distribution du champ magnétique dans l’espace.
Dans les expériences on utilise les appareils suivants :
* détecteur synchrone: permet d'extraire un signal périodique à la fréquence de travail noyé dans des bruits à d'autres fréquences.
 |
 |
 |
Le capteur Honeywell HMC1001 est un circuit intégré détecteur de champ magnétique B par effet de magnétorésistance. Il permet de mesurer l'amplitude de B suivant une orientation repérée sur le boitier.
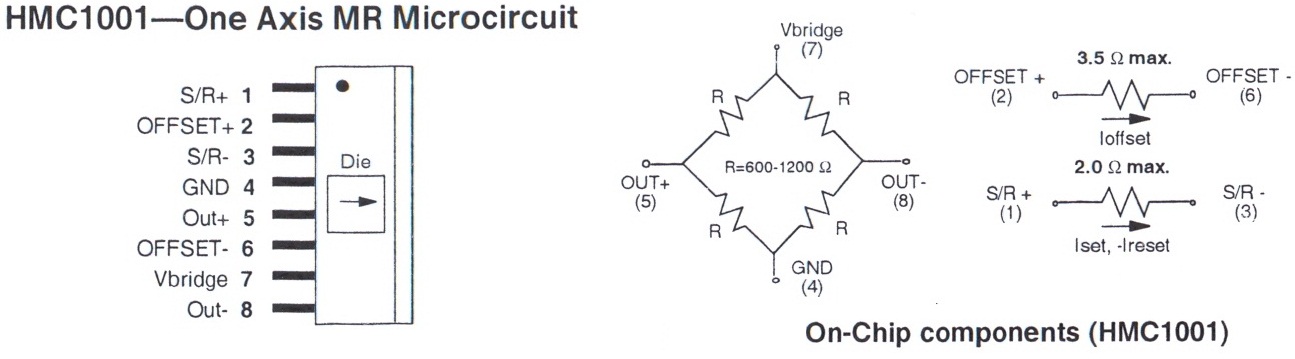
Le cœur du capteur est un pont de Wheatstone dont les branches sont des éléments résistants en Permalloy (Ni-Fe) déposés sur un wafer de silicium.
La couche de Permalloy est constituée par des domaines magnétiques dont les vecteurs aimantation sont orientés de manière aléatoire. Ces domaines peuvent être réalignés à l'aide d'une forte impulsion de champ magnétique (>3Gauss) produite par un courant bref circulant dans une résistance annexe et intégrée au capteur. Cette opération (set) accroît la sensibilité, la linéarité et la reproductibilité; de plus, une impulsion en sens inverse (reset) oriente les domaines en opposition, ce qui permet de s'affranchir d'éventuels décalages ou dérives.
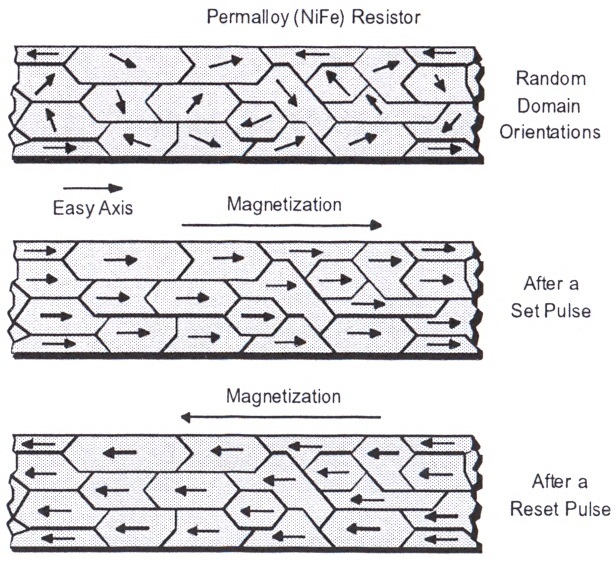
Au cours de la mesure, le champ B modifie réversiblement l'orientation des domaines, ce qui provoque une variation de résistance elle-même détectée par le pont de Wheatstone ce qui signifie que la résistance varie en fonction de l’orientation du vecteur aimantation modifiée par le champ B : f(M.B).
Pour les mesures de champs statiques: on procède à deux lectures 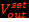 et
et  et le constructeur indique
et le constructeur indique 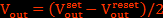 . La sensibilité s du capteur (s = 16mV/Gauss pour une alimentation de 5 volts est donnée par le constructeur) permet d’en déduire B. On peut mesurer des champs magnétiques d'une amplitude maximum de 2 Gauss avec une résolution de 10 mGauss. Par précaution, on a étalonné le capteur sur des champs magnétiques connus.
. La sensibilité s du capteur (s = 16mV/Gauss pour une alimentation de 5 volts est donnée par le constructeur) permet d’en déduire B. On peut mesurer des champs magnétiques d'une amplitude maximum de 2 Gauss avec une résolution de 10 mGauss. Par précaution, on a étalonné le capteur sur des champs magnétiques connus.
Pour les mesures de champs magnétiques sinusoïdaux: on oriente les domaines magnétiques (set) avant la mesure, puis on enregistre l'oscillation de 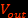 avec un voltmètre TRMS (True Root Mean Square) ou un détecteur synchrone. Les spécifications indiquent une bande passante de 5MHz, ce qui ne pose aucun problème pour nos mesures qui ne dépassent pas 20 kHz.
avec un voltmètre TRMS (True Root Mean Square) ou un détecteur synchrone. Les spécifications indiquent une bande passante de 5MHz, ce qui ne pose aucun problème pour nos mesures qui ne dépassent pas 20 kHz.
Les dimensions du solénoïde :
En faisant passer un courant continu dans le solénoïde on mesure la tension à ses bornes pour en déduire ensuite la résistance Rsol=0,481±0,001 Ohms.
En faisant passer un courant alternatif dans le solénoïde on mesure la tension à ses bornes en fonction de la fréquence d’où on en déduit l’inductance Lsol=1,00±0,02 mH. 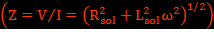

Tout d’abord on observe l’effet Maxwell-Lodge en utilisant les instruments et le montage décrits ci-dessous: le signal sinusoïdal crée par un générateur de fonction est amplifié et alimente le solénoïde en régime alternatif; autour de lui à mi-hauteur, on place les spires ouvertes de différents diamètres qui sont reliées à l’oscilloscope. Puis, on effectue une série de mesures de tension V dans ces spires en fonction de la fréquence. Le courant alternatif alimentant le solénoïde est d’intensité efficace 1.01±0,01 A.
| d (cm) | f±1 (Hz) | V (mV) | ∆V (mV) | Vth (mV) | ∆Vth (mV) |
| 15,2 | 209 | 3,2 | 0,2 | 4,0 | 0,2 |
| 590 | 9,2 | 0,4 | 11,3 | 0,4 | |
| 1008 | 16 | 1 | 19,3 | 0,7 | |
| 1241 | 19 | 1 | 23,7 | 0,9 | |
| 1487 | 23 | 1 | 28 | 1 | |
| 25,2 | 213 | 3,8 | 0,2 | 4,1 | 0,2 |
| 599 | 10,4 | 0,4 | 11,5 | 0,4 | |
| 991 | 17 | 1 | 19,0 | 0,7 | |
| 1250 | 21 | 1 | 23,9 | 0,9 | |
| 1500 | 25 | 1 | 29 | 1 | |
| 30,1 | 199 | 3,0 | 0,2 | 3,8 | 0,2 |
| 600 | 8,8 | 0,4 | 11,5 | 0,4 | |
| 995 | 15 | 1 | 19,0 | 0,7 | |
| 1240 | 18 | 1 | 23,7 | 0,9 | |
| 1520 | 22 | 1 | 29 | 1 |
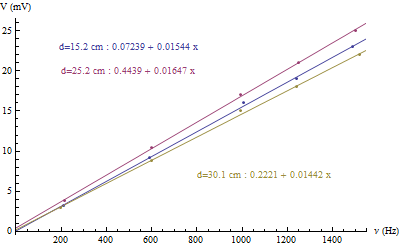
Directement on remarque que la tension mesurée ne dépend pas du rayon des spires. Vth est la force électromotrice théorique calculée en fonction des paramètres du solénoïde. La dépendance en fréquence est linéaire.
Les écarts entre les valeurs de tensions expérimentale et théorique peuvent être expliqués par l’auto-inductance des spires, la fuite du champ magnétique. De plus, cela peut expliquer aussi une légère diminution de la tension dans une spire en fonction de son rayon.
Puis, avec un montage similaire en prenant une bobine de 320 spires on mesure la force électromotrice en fonction de la fréquence en utilisant un multimètre. On fait une série de mesures pour des courants différents.
| I±0,1 (A) | f±1 (Hz) | V±0,1 (V) | Vth (V) | ∆Vth (V) |
| 1,0 | 203 | 1,3 | 1,2 | 0,1 |
| 602 | 3,8 | 3,7 | 0,3 | |
| 1007 | 6,4 | 6,2 | 0,5 | |
| 1303 | 8,5 | 8,0 | 0,6 | |
| 1518 | 9,9 | 9,3 | 0,7 | |
| 1,5 | 203 | 1,9 | 1,9 | 0,1 |
| 602 | 5,7 | 5,5 | 0,3 | |
| 1007 | 9,6 | 9,2 | 0,6 | |
| 1303 | 12,4 | 12,0 | 0,7 | |
| 1518 | 14,6 | 13,9 | 0,8 | |
| 2,0 | 203 | 2,6 | 2,5 | 0,1 |
| 602 | 7,9 | 7,4 | 0,4 | |
| 1007 | 12,9 | 12,3 | 0,6 | |
| 1303 | 16,8 | 16,0 | 0,8 | |
| 1518 | 19,9 | 18,6 | 1,0 |
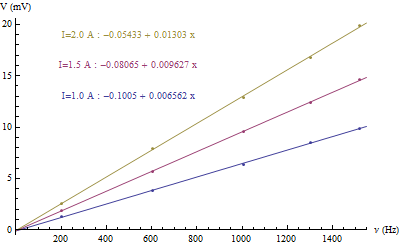
Comme la bobine contient 320 spires on trouve bien une tension environ 320 fois plus grande que celle observée pour une seule spire. De même que dans le cas précédent la variation de la force électromotrice est bien linéaire en fonction de la fréquence du courant alternatif. Dans les deux cas, on observe la linéarité de la tension dans la spire ou la bobine avec le courant traversant le solénoïde.
Précédemment, les expériences suivantes ont été réalisées pour mettre en evidance la dépendance de la manière de mesure de la tension : selon un arc de circuit ou son complémentaire dans la spire.
| Dispositif expérimental |
| Mesures de la force électromotrice induite dans une spire ouverte externe | Mesures de la force électromotrice induite dans une spire ouverte externe |
la force électromotrice induite ne dépend pas du rayon de la spire
| Mesures de la force électromotrice induite dans 1/3 de spire fermée externe | Mesures de la force électromotrice induite dans 2/3 de spire fermée externe |
la force électromotrice induite, correspondant à la circulation du potentiel vecteur, dépend de l'arc suivant lequel on fait la mesure
Ensuite, on réalise un montage où le solénoïde est mis dans un blindage magnétique fermé. Mais dans ce cas là on trouve la tension dans la bobine de l’ordre de 10 mV et dans la spire elle n’est pas détectable par le multimètre.
Cet effet a aussi été observé dans des expériences faites précédemment avec un blindage électrostatique fermé [2]. Son explication est que des courants induits apparaissent dans le blindage qui contrarient l’effet du courant dans le solénoïde. Pour éviter ces courants il faut que le blindage soit fendu.
On va étudier cet effet sur la distribution du champ magnétique dans l’espace.
On va mesurer le champ magnétique créé par le solénoïde dans deux régimes : avec un courant continu ou alternatif. Dans le premier cas on alimente le solénoïde avec un générateur de courant continu, dans le deuxième avec un générateur de fonction suivi par un amplificateur.
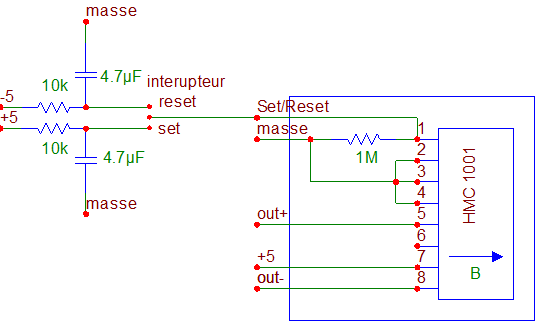
Le circuit du capteur de champ magnétique est réalisé suivant le schéma présenté. Le capteur est alimenté par un bloc ±5V branché au secteur. Les pulses pour set et reset sont fait à l’aide des circuits RC en exploitant la décharge du condensateur après la fermeture du circuit par l’interrupteur.
 |
 |
 |
En mettant le capteur magnétique à l’intérieur du solénoïde et à la moitié de sa hauteur, on mesure les tensions de sortie  et
et 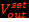 en variant le courant traversant le solénoïde de 0 à 0,5 A. On obtient
en variant le courant traversant le solénoïde de 0 à 0,5 A. On obtient 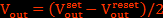 . En connaissant la valeur théorique de champ magnétique à l’intérieur du solénoïde, on étalonne la sensibilité du capteur qui est
. En connaissant la valeur théorique de champ magnétique à l’intérieur du solénoïde, on étalonne la sensibilité du capteur qui est
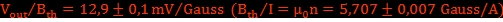
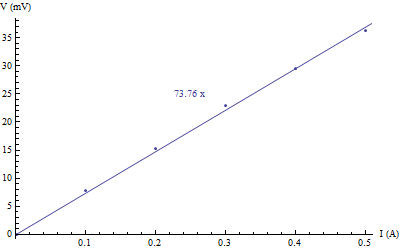
| I (A) | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| Vout (mV) | 0,00 | 7,79 | 15,20 | 22,90 | 29,45 | 36,20 |
| Bth (G) | 0,000 | 0,571 | 1,141 | 1,712 | 2,283 | 2,854 |
En utilisant la sensibilité trouvée on mesure le champ magnétique à l’extérieur du solénoïde en orientant le capteur magnétique selon 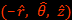 correspondant aux vecteurs unitaires de la base cylindrique. Puis, dans le traitement des données, on normalise le module du champ magnétique trouvé par rapport au champ théorique à l’intérieur du solénoïde. On augmente le courant (1A, 5A et 9A) pour obtenir des valeurs du champ détectables à l’extérieur du solénoïde. Il s’ensuit des valeurs du champ à l’intérieur trop fortes pour être mesurées avec le capteur.
correspondant aux vecteurs unitaires de la base cylindrique. Puis, dans le traitement des données, on normalise le module du champ magnétique trouvé par rapport au champ théorique à l’intérieur du solénoïde. On augmente le courant (1A, 5A et 9A) pour obtenir des valeurs du champ détectables à l’extérieur du solénoïde. Il s’ensuit des valeurs du champ à l’intérieur trop fortes pour être mesurées avec le capteur.
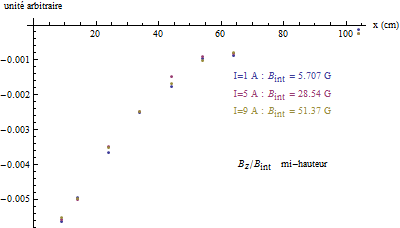
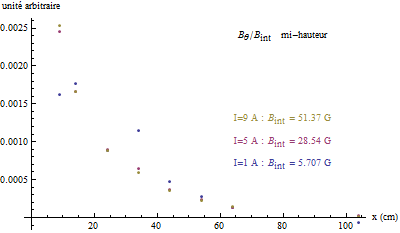
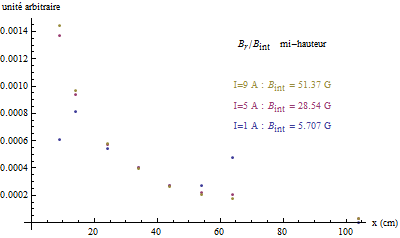
On effectue une série de mesures du champ magnétique en fonction de la distance par rapport au centre du solénoïde d’abord à mi-hauteur puis au bord en déplaçant le capteur perpendiculairement à l’axe du solénoïde.
 |
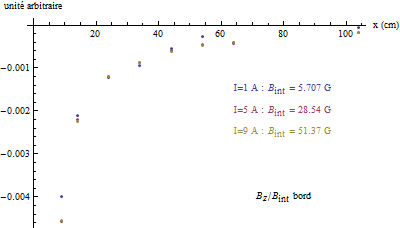 |
 |
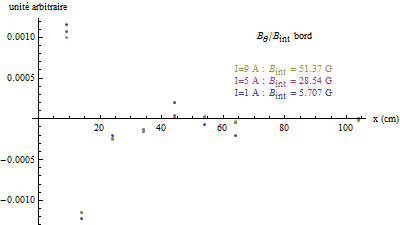 |
 |
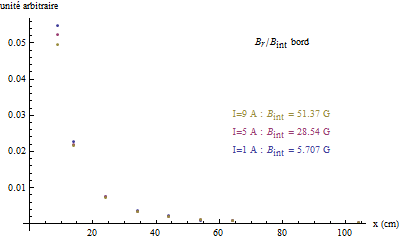 |
Dans le cas où le solénoïde est entouré par un blindage électrostatique ouvert (cylindre de laiton fendu) et les mesures sont réalisées à mi-hauteur, on trouve que le champ magnétique est le même à 0.1% près.
suivant z :
| (Bz(1A)-Bz(0A))/Bint (%) | -0,42 | -0,36 | -0,26 | -0,18 | -0,11 | -0,09 | -0,05 | -0,01 |
| (Bz(5A)-Bz(0A))/Bint (%) | -0,41 | -0,36 | -0,26 | -0,17 | -0,12 | -0,08 | -0,06 | -0,02 |
| (Bz(9A)-Bz(0A))/Bint (%) | -0,41 | -0,36 | -0,25 | -0,17 | -0,12 | -0,08 | -0,06 | -0,02 |
suivant θ :
| (Bθ(1A)-Bθ(0A))/Bint (%) | 0,06 | 0,07 | -0,02 | 0,01 | 0,02 | 0,02 | 0,01 | 0,00 |
| (Bθ(5A)- Bθ(0A))/Bint (%) | 0,08 | 0,04 | 0,01 | 0,01 | 0,01 | 0,01 | 0,00 | 0,00 |
| (Bθ(9A)- Bθ(0A))/Bint (%) | 0,08 | 0,04 | 0,01 | 0,01 | 0,01 | 0,00 | 0,00 | 0,00 |
suivant r :
| -(Br(1A)-Br(0A))/Bint (%) | -0,07 | -0,03 | -0,02 | -0,04 | -0,03 | -0,01 | 0,01 | -0,04 |
| -(Br(5A)-Br(0A))/Bint (%) | -0,07 | -0,07 | -0,05 | -0,04 | -0,03 | -0,02 | -0,01 | -0,01 |
| -(Br(9A)-Br(0A))/Bint (%) | -0,07 | -0,08 | -0,05 | -0,04 | -0,03 | -0,02 | -0,01 | -0,01 |
Dans le cas où le solénoïde est entouré par un blindage magnétique fermé, le champ magnétique est nul.
 |
 |
Pour ce cas on n’a plus besoin des pulses "set" et "reset" pour faire les mesures de champ magnétique. On mesure l’amplitude de la tension de sortie du capteur directement sur l’oscilloscope ou sa valeur efficace à l’aide d’un voltmètre. Comme il s’agit de signaux d’amplitude faible, on observe un signal parasite de 50 Hz à cause du secteur. Le parasite disparaît en utilisant, comme alimentation, une pile de 4,5 V.
Comme précédemment, on mesure le signal du capteur dans le solénoïde pour les courants variant de 0.1 à 0.5 A afin d’étalonner la sensibilité du capteur.
| I (A) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| mV/Gauss | 11,88 | 11,69 | 11,39 | 10,98 | 10,43 |
On observe la saturation du capteur pour un fort courant. Donc, on prend cela en compte pour les mesures de champ magnétique dans la suite. De plus, d’après cette expérience, il n’y a pas de dépendance en fréquence pour la tension de sortie du capteur.
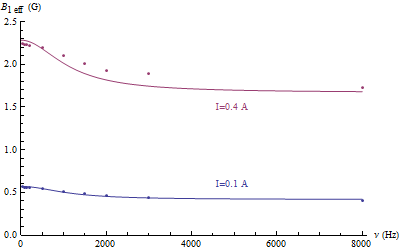
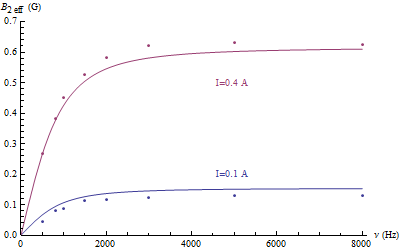
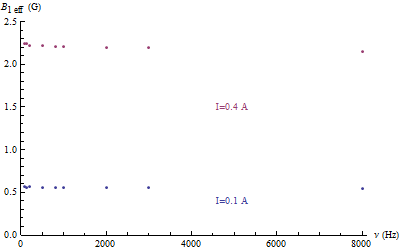
Ensuite on mesure les tensions de sortie du capteur à l’intérieur du solénoïde et entre le solénoïde et le blindage électrostatique fermé. On déduit le champ magnétique noté 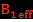 pour le premier cas et
pour le premier cas et 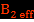 pour le second. Sur le graphe avec les points expérimentaux, on trace les courbes issues de l’analyse théorique (cf. plus loin). On constate un bon accord entre les résultats expérimentaux et théoriques.
pour le second. Sur le graphe avec les points expérimentaux, on trace les courbes issues de l’analyse théorique (cf. plus loin). On constate un bon accord entre les résultats expérimentaux et théoriques.
 |
 |
Comme auparavant, l’expérience est réalisée aussi avec le blindage magnétique fermé. Pour les mesures du champ magnétique 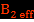 entre le solénoïde et ce blindage le signal du capteur est inférieur à 1 mV ce qui est du même ordre de grandeur que les signaux parasites générés par les fils parcourus par un fort courant. On s’affranchit des parasites en remplaçant les fils de mesure par des câbles blindés. Les mesures de ces signaux de faible amplitude sont faites à l’aide d’un détecteur synchrone.
entre le solénoïde et ce blindage le signal du capteur est inférieur à 1 mV ce qui est du même ordre de grandeur que les signaux parasites générés par les fils parcourus par un fort courant. On s’affranchit des parasites en remplaçant les fils de mesure par des câbles blindés. Les mesures de ces signaux de faible amplitude sont faites à l’aide d’un détecteur synchrone.
 |
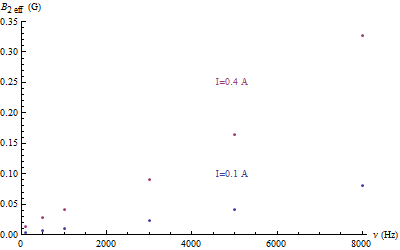 |
On constate que dans le solénoïde entouré par le blindage magnétique fermé le champ magnétique est indépendant de la fréquence du courant, alors que dans la région entre le solénoïde et le blindage magnétique fermé il augmente. Or, pour le blindage électrostatique fermé dans les deux régions l’indépendance de la fréquence du courant apparaît après 2 kHz.

Riemann a postulé (en combinant l'équation de d'Alembert (sans terme source) avec l'équation de Poisson (sans terme propagatif)) que les phénomènes électromagnétiques sont décrit par :
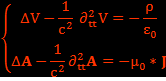
Avec ses équations et avec l’équation de conservation de la charge : 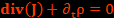 , on trouve bien les équations de Maxwell :
, on trouve bien les équations de Maxwell :  connus =>
connus =>  calculés =>
calculés =>  définis.
définis.
En particulier, à partir de l’équation de conservation de la charge et en faisant la réduction dite de "Levi-Civita" on retrouve la contrainte "de Lorenz" (avec 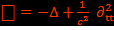 ) :
) :
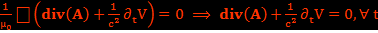
On obtient deux équations de Maxwell à partir de la définition de 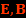 :
:
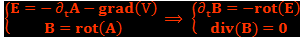
En prenant la limite galiléenne de la contrainte de Lorenz pour les basses vitesses v<<c on trouve la contrainte de Coulomb. En effet, en utilisant l’analyse dimensionnelle, on regarde le rapport de ces deux termes :
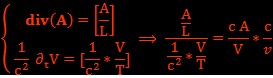
On voit qu’il existe deux cas possibles (v<<c) [3,4,5] :
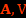 et en utilisant les relations suivantes :
et en utilisant les relations suivantes : 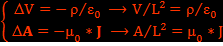 on a ρ*c>>J ce qui est le cas des isolants. Donc c’est le cas de la limite galiléenne électrique. Donc, dans le cas de cette limite, les deux équations de Maxwell deviennent :
on a ρ*c>>J ce qui est le cas des isolants. Donc c’est le cas de la limite galiléenne électrique. Donc, dans le cas de cette limite, les deux équations de Maxwell deviennent : 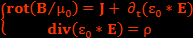
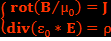 Ce cas, pour lequel J>>ρ*c, correspond au domaine d'étude de l'effet Maxwell-Lodge car ρ=0 dans un conducteur ohmique comme le solénoïde.
Ce cas, pour lequel J>>ρ*c, correspond au domaine d'étude de l'effet Maxwell-Lodge car ρ=0 dans un conducteur ohmique comme le solénoïde.Pour le solénoïde parfait de rayon R, le champ magnétique est 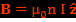 . Par symétrie, le potentiel vecteur est de la forme
. Par symétrie, le potentiel vecteur est de la forme 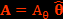 . En coordonnées cylindriques, on obtient l’équation différentielle à partir de laquelle on calcule le potentiel vecteur dans l’espace :
. En coordonnées cylindriques, on obtient l’équation différentielle à partir de laquelle on calcule le potentiel vecteur dans l’espace :
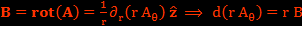
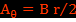
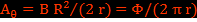 avec le flux magnétique
avec le flux magnétique 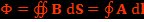
D’où on trouve la force électromotrice pour une spire de rayon r autour du solénoïde parcouru par un courant de la forme 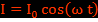 :
:
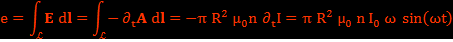
Donc on voit que la force électromotrice est indépendante de rayon d'une spire
Le modèle suivant a été développé au cours du projet en laboratoire.
Le Solénoïde de rayon R, comportant n spire/m est parcouru par un courant 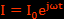 . Il est entouré par un blindage de rayon R', d'épaisseur a<<R' et de conductivité γ.
. Il est entouré par un blindage de rayon R', d'épaisseur a<<R' et de conductivité γ.
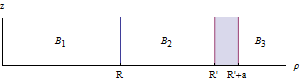
A un temps t donné, le théorème d’Ampère permet d’écrire :
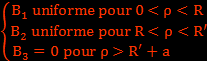
On a les relations de passage (en cylindriques) :
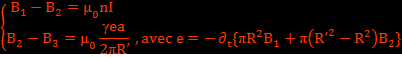
Comme le blindage est fermé et d’épaisseur très faible, il est parcouru par un courant de surface dû au potentiel vecteur externe au solénoïde qui varie temporellement. Le potentiel vecteur est continu aux interfaces.
En éliminant B1 entre les deux relations de passage on obtient l'équation différentielle :
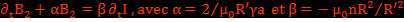
α est l’inverse du temps de diffusion du champ magnétique.
En posant 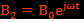 , on obtient
, on obtient 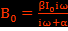 . Donc
. Donc
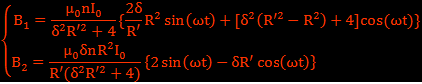
avec 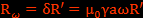 qui est le paramètre d’écrantage [6].
qui est le paramètre d’écrantage [6].
Avec les données du blindage laiton, on remarque que Rω=1 pour υ=392 Hz ce qui n'est pas négligeable devant 4. Dans ce cas, cette quantité montre que le champ ne peut pénétrer dans le métal que sur une courte distance avant que sa direction ne soit inversée. Rω<<1 signifie la pénétrabilité totale, Rω>>1 qu’il n’y a pas de pénétration. [6]
Expérimentalement, c'est la valeur efficace du champ magnétique que l'on mesure, c'est-à-dire 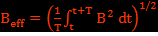 , on l’obtient sous la forme suivante :
, on l’obtient sous la forme suivante :
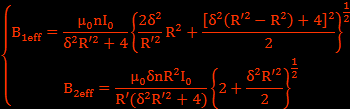
Dans le cas du blindage magnétostatique, il faut prendre en compte l'aimantation dans le blindage pour écrire correctement les équations des champs magnétiques. Ce sera l'objet d'une étude ultérieure.
Après avoir examiné les résultats expérimentaux et en les comparant à la théorie, on trouve une bonne cohérence entre eux.
L’apparition d’une force électromotrice dans les spires de différents rayons et dans la bobine de 320 spires peut s’expliquer par l’existence du potentiel vecteur dans l’espace doublement connexe qui est créé par le solénoïde parcouru par un courant alternatif. De plus, en théorie cette force électromotrice ne dépend pas du rayon de la boucle entourant le solénoïde ce qui est bien vérifié expérimentalement comme le montre la mesure de la tension dans plusieurs spires de diamètres différents. En revanche, on obtient des valeurs différentes de la tension suivant la manière de mesurer selon un arc de circuit ou son complémentaire dans la spire (c'est-à-dire selon la longueur de cet arc lui-même, autrement dit de la position des points de mesure du voltmètre sur la spire et du côté où on passe ses fils) (cf. films).
Le modèle théorique décrit bien l’effet de blindage par les courants induits. Le potentiel vecteur doit traverser un blindage magnétique car il est continu aux interfaces. Or, on ne mesure pas de f.é.m. à l’extérieur du blindage dans la spire. Si le blindage est fermé, des courants induits apparaissent. Il existe donc un potentiel vecteur induit crée dans le blindage qui s’oppose au potentiel vecteur dû au solénoïde. C’est pourquoi, les auteurs de [2] avaient remarqué cette influence avec le blindage électrique fermé. On s’attend donc à ce que l'ouverture du blindage magnétique empêche l'apparition d'un potentiel vecteur induit. Cependant, le mu-métal perd une partie de ses propriétés de blindage magnétique lorsqu'il subit une modification mécanique comme une découpe.
Les mesures du champ magnétique avec le blindage électrostatique fermé sont conformes aux prédictions de la théorie développée au cours de ce projet. En revanche, on ne peut pas dire grand chose sur les résultats expérimentaux obtenus avec le blindage magnétique: il faudra intégrer le courant d’aimantation dans les équations. Donc, on ne peut constater que deux choses :
Enfin, les mesures du champ magnétique faites en régime continu montrent qu’il est petit à mi-hauteur du solénoïde contrairement à son bord ce qui justifie que l’on réalise les mesures de la force électromotrice dans cette zone.
Après ce travail, on doit conclure que l’effet Maxwell-Lodge n’est explicable qu’en révisant la théorie électromagnétique pour donner un rôle plus important aux potentiels. Il faut s’interroger sur l’importance physique du potentiel vecteur en prenant en compte nos résultats théoriques et nos mesures expérimentales. Comme dans l'effet Aharonov-Bohm en mécanique quantique où la prise en considération du potentiel vecteur est maintenant acceptée, on pense qu’il doit en être de même en électromagnétisme classique avec l’effet Maxwell-Lodge. Le potentiel vecteur serait véritablement le phœnix de l’électromagnétisme.
Il y a encore du travail à faire pour intégrer définitivement l'importance du potentiel vecteur, en particulier se pose le problème de sa mesure directe qui, à notre connaissance, n’a toujours pas été faite ; l’effet Maxwell-Lodge peut être considéré comme une mesure indirecte de ce potentiel vecteur. Une expérience importante à faire dans l’avenir est la mesure de la force électromotrice dans une spire ou une bobine entourant le solénoïde lui-même entouré par un blindage magnétique ouvert c'est-à-dire fendu pour empêcher la circulation des courants induits. On pourra ainsi séparer les contributions magnétique et induite du blindage. Nous n’avons pas pu le faire car fendre le blindage en mu-métal lui fait perdre ses propriétés magnétiques que l’on ne peut recouvrer que par un traitement thermique. Nous avons seulement pu étudier son fonctionnement lorsqu'il est fermé.
On a, en revanche, bien avancé dans le cas du blindage électrostatique: la mise au point d’un détecteur de champ magnétique sensible nous a permis d’effectuer des mesures fiables et le développement théorique associé s’est révélé en bon accord avec l’expérience. On pourra plus tard étudier le déphasage qui apparaît en sinusoïdal entre la source (courant dans le solénoïde) et les champs magnétiques qui existent dans les différentes régions de l’espace.
Le projet en laboratoire a pour but de faire comprendre le travail de chercheur et d'illustrer les différentes étapes du processus de recherche. Donc on s'est mis dans la peau pour mieux en avoir idée.
Le projet traité par notre groupe comportait une partie théorique et une partie expérimentale. Un telle répartition du projet nous a permis de découvrir à la fois le travail d’un théoricien et d’un expérimentateur. La partie théorique dirigée par Germain Rousseaux nous a ouvert à un tout nouveau point de vue sur l'électromagnétisme qui n'est pas enseigné dans les cours classiques. Dans la partie expérimentale Richard Kofman nous a montré que les connaissances du chercheur expérimentateur doivent s'étendre au delà de sa spécialité, c'est-à-dire, par exemple, il faut connaître l'électronique en plus de la physique dont on est spécialisé (pour faire fonctionner le capteur du champ). Au cours des expériences, on a appris qu’il faut être sceptique et bien connaître le fonctionnement des appareils de mesure.
Le thème de ce projet est très intéressant et touche la physique fondamentale. Plus précisément, la théorie électromagnétique peut-être aborder de différents points de vue dont certains sont plus accessibles à la compréhension. Les différentes approches peuvent donc faire émerger une explication à des phénomènes mal connues.
Ce type de travail est passionnant et éducatif, et montre le chemin à la compréhension de la physique fondamentale, donc de la Nature.