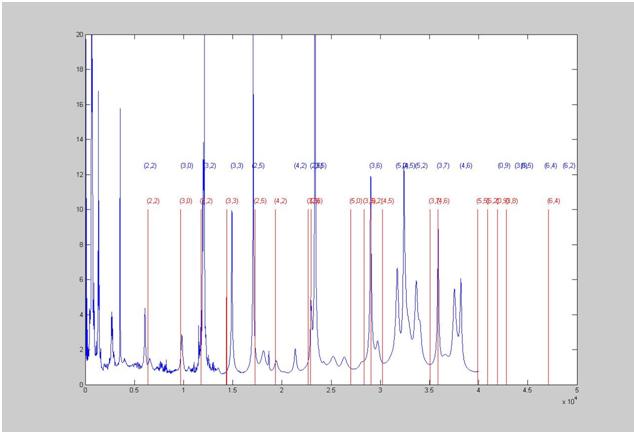
Ce programme a pour but d'afficher la fréquence des différents modes propres aussi bien théoriques qu’expérimentaux. Puis il superpose les fréquences sur un même graphique.

Voici le code réalisé sous Matlab, qui nous a permit de faire ce programme avec le résultat obtenue.


clear all
figure
h=.352/2;
Vt=4670;
Vl=9134;
a=5.2e-2;
b=3.6e-2;
dx=0.01e-2;
x=0:dx:a;
y=0:dx:b;
e=450e9;%modul d'young
%h=352e-6;%epaisseur suposé a changer!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
nu=0.42;%coef poisson
rho=2330;%masse volumique

d1='C:\Documents and Settings\visiteur\Bureau\l3 projet plaque metalique\programme expérience\tfv tt points\nouveaux resultats\';
load([d1,'tfv1.mat'])
aa= squeeze(mean(mean(abs(tfv(10:158,10:95,:))))); %moyenne
load([d1,'tfv1001.mat'])
aa= squeeze(mean(mean(abs(tfv(10:158,10:95,:))))); %moyenne
% load([d1,'tfv2001.mat'])
aa= squeeze(mean(mean(abs(tfv(10:158,10:95,:))))); %moyenne

% load([d1,'tfv3001.mat'])
aa= squeeze(mean(mean(abs(tfv(10:158,10:95,:))))); %moyenne

% load([d1,'tfv4001.mat'])
aa= squeeze(mean(mean(abs(tfv(10:158,10:95,:))))); %moyenne
load([d1,'tfv5001.mat'])
aa= squeeze(mean(mean(abs(tfv(10:158,10:95,:))))); %moyenne

masse=rho*h;
 D=e*h^3/(12*(1-nu^2));
 plot(f1(1:1000),aa)
 ylim([0 20])
%  xlim([0 25000])
nm=8; %nombre de mode
reso=[6060 9800 12120 14900 17080 21320 22960 23360];
order=[2 2;3 0;3 2;3 3;2 5;4 2;2 6;3 5];
for ii=1:nm
text(reso(ii)-100,12.5,['(',num2str(order(ii,1)),',',num2str(order(ii,2)),')'],'Color','b')
end


hold on




i=1
  for m=0:5;
  for n=0:5;
%for ii=1:nm
   % m=order(ii,1);
    %n=order(ii,2);
   
if m~=0 || n~=0 

%i=1+i;
wx=cos(m*pi*x/a);
wy=cos(n*pi*y/b);

k=sqrt((n*pi/a)^2+(m*pi/b)^2);
Vp=2*Vt*(1-(Vt^2/Vl^2));
ohmega=1.27*(Vp./sqrt(3)).*k.^2*h*1e-3;
freqreel=ohmega/(2*pi);

 fre=freqreel;
 fre=round(fre);
vectfre=zeros(1,20000);
vectfre(fre)=10;
plot(vectfre,'r')
text(fre-100,10.5,['(',num2str(m),',',num2str(n),')'],'Color','r')
hold on
drawnow,
 end
 end
 end

Retour en haut de la page.