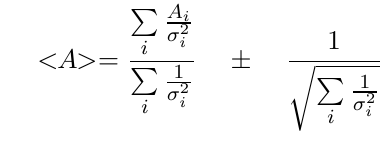Les fichiers sources ne sont pas tout de suite exploitable du fait du fonctionnement du programme :
- Lors de l'acquisition des données, chaque particule est dans un premier temps sélectionnée à la souris. Le temps que chaque particule soit pointée, le nombre de particules enregistrées par le programme est différent de celui de l'expérience en cours.
- De plus, et particulièrement si la particule est proche du bord du piège, le programme peut perdre une particule, l'opérateur doit alors pointer à nouveau la particule, entraînant un trou dans les mesures.
| Temps | x1 y1 c1 | x2 y2 c2 | … | … | … | … | … |
Afin de pouvoir comparer les résultats, on calcule une donnée unique : le centre de masse de l'ensemble des particules.
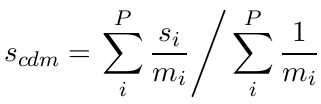
- scdm : Coordonnée du centre de masse, représente x ou y.
- si : Coordonnée de la particule i, représente x ou y.
- mi : Masse de la particule i (ici, toutes les particules ont la même masse)
- P : nombre total de particules
Pour faire de bons calculs statistiques, notamment pour un procédé stochastique tel le mouvement Brownien, il faut un grand nombre de mesures. Une méthode consiste à travailler avec un grand nombre de particules
On va donc travailler avec des fichiers très long, que l'on coupe selon des intervalles de points Δn (corrrspondant à un temps caractéristique τ=Δn x Δt, Δt étant l'intervalle de temps moyen entre chaque mesure ~ 0,1 s) à partir d'un point de réfèrence mi=i x Δn.
Pour pouvoir utiliser cette méthode, on suppose le procédé ergodique : on obtient le même résultat en faisant la moyenne sur Q objets, on obtient le même résultat qu'avec un même objet représenté par Q intervalles de temps indépendant. De plus, pour que les procédés soient indépendant, on doit choisir Δn tel que τ soit supérieur au temps de corrélation (donnée de l'expérience approximativement égal à 5 s) et au temps de saturation .
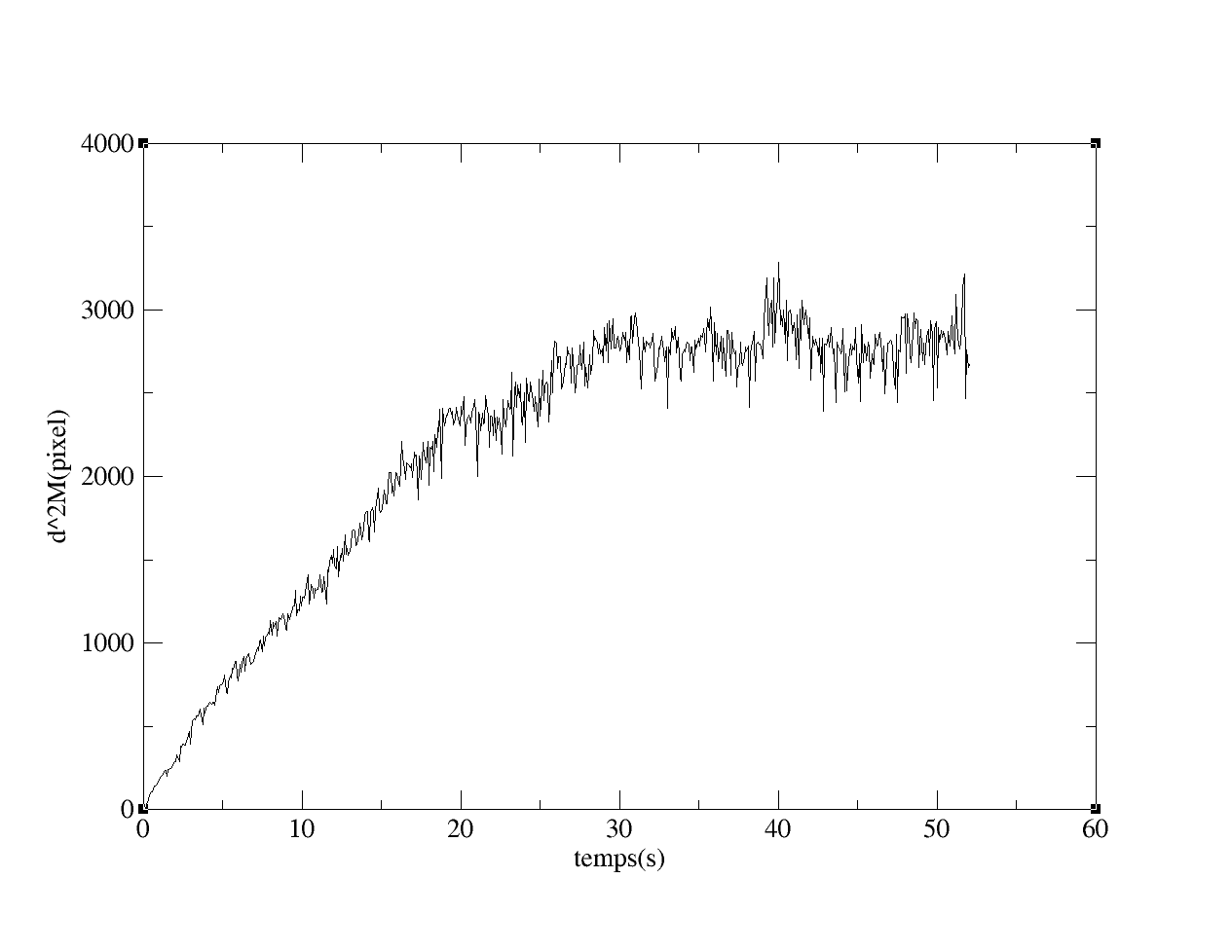
Calcul, sur un intervalle de 600 points de d2m, on voit bien les deux parties de la courbe et le temps de saturation ~ 30 s.
| Intervalle Δ n | Pente |
| 100 | (1,9 +/- 0,2).102 |
| 200 | (1,9 +/- 0,7).102 |
Le mouvement Brownien est caractérisé par une statistique poissonienne, nous allons vérifier que notre expérience vérifie bien cette condition, condition sine qua non à un traitement plus approfondie des données.
On trace donc, pour chaque courbe fi, (xm,i et ym,i : cooordonnées de la particule mi de référence) :
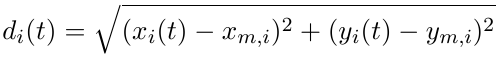
.png)
Une représentation de di en fonction du temps
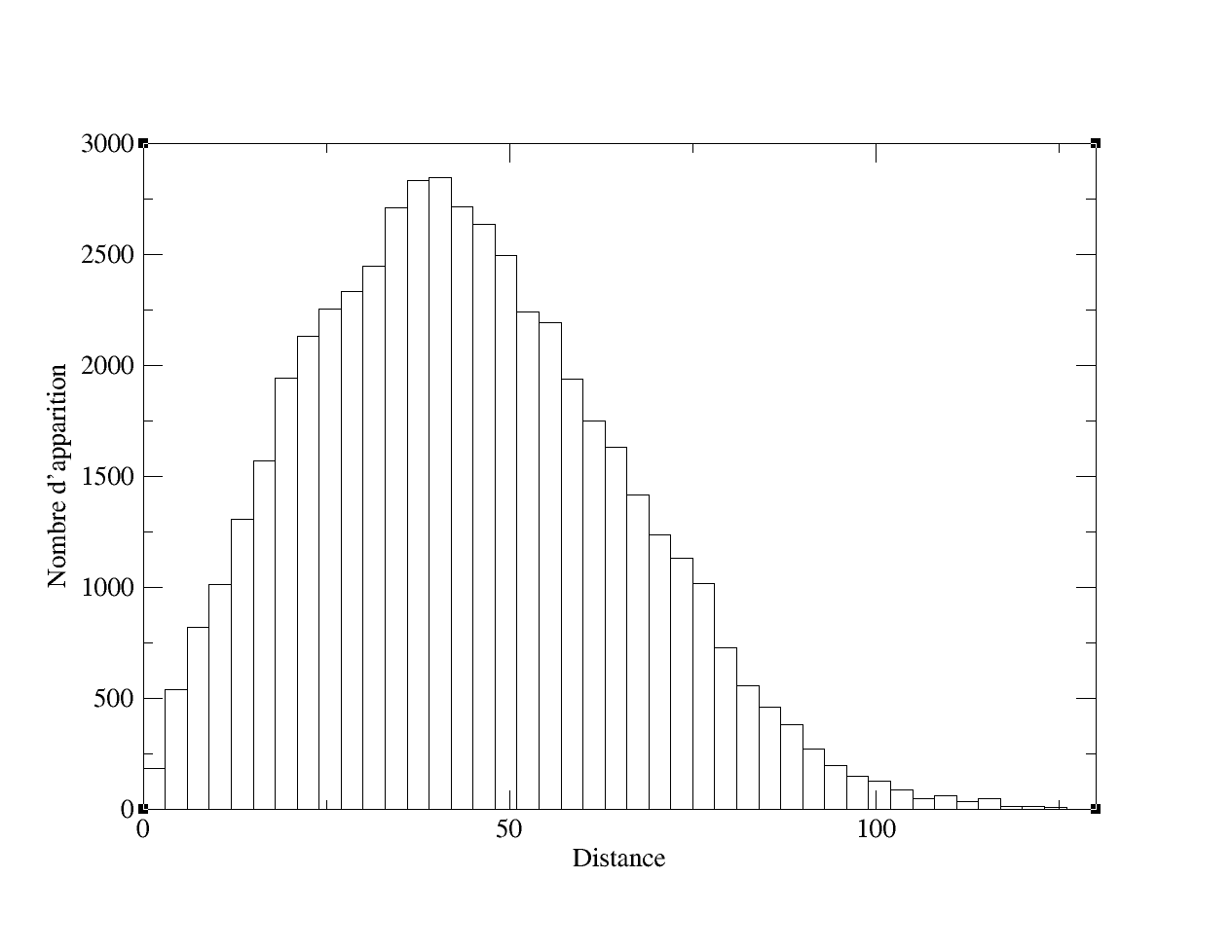
Histogramme des distances moyennes
Ceux qui caractérise le mouvement Brownien est le coefficient de diffusion D=< x2 >/2t. On va donc calculer :
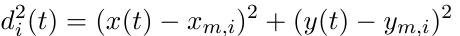
Les intervalles de temps entre deux points successifs n'étant pas constant (problème dû au fait que les traitements de données ne prennent pas toujours le même temps et que le système d'exploitation prend de temps en temps la précédence sur les calculs) on va déterminer un intervalle de temps moyen fixe ΔtM=ttot/N (N: nombre total de points) que l'on diminue un peu (x0,9) tel que chaque intervalle ΔtM ne contient au plus, qu'un seul point d2i pour chaque courbe fi. On a donc, pour chaque ΔtM, une série de d2i(tj)(tj=j.ΔtM) dont on calcule la moyenne sur tous les i, c'est-à-dire, la courbe des distances au carrée moyenne d2M(tj) à intervalle de temps ΔtM.
b.png)
Calcul de d2M (t). La saturation n'est pas atteinte mais on a démontré au dessus que cela ne modifiait pas l'estimation du coefficient de diffusion.
Du fait de la manière empirique de situer la frontière entre la partie Brownienne et la partie saturée, de grandes erreurs sont introduites par cette méthode. Donc, pour limiter cette erreur, on coupe le fichier de données en plusieurs fichiers de taille comparable. Ces fichiers subissent le même traitement, ce qui nous donne plusieurs pentes A i, d'écart-type σi, à partir desquels on calcule une moyenne pondérée < A >, proportionnelle au coefficient de diffusion.