Modèle standard
Pour rendre compte des phénomènes de génération de paires/piégeage/recombinaison, on s’appuie le plus souvent sur un ensemble d’équations différentielles couplées régissant les variations élémentaires de toutes les populations en fonction du temps. Ce modèle est celui qui est utilisé le plus couramment. Au regard des observations précédentes, on peut ne retenir qu’un seul centre de recombinaison (Yb3+) et plusieurs pièges. Par commodité, nous avons préféré utiliser des pièges à électrons plutôt que des pièges à trou. Cela ne change rien, car les phénomènes physiques mis en jeu sont les même (problème totalement symétrique). On obtient ainsi le schéma énergétique de la figure suivante et les équations suivantes qui lui sont associées.
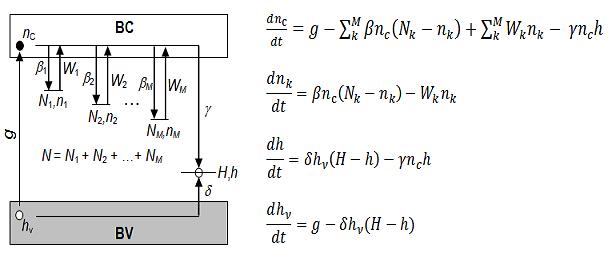
Des simplifications peuvent être introduites selon qu’on se trouve à l’étape d’irradiation et de remplissage de pièges ou de la lecture TL. On utilise les définitions suivantes :

Pour le modèle on fait l’hypothèse que tous les pièges présentent le même coefficient de piégeage β. Pour limiter le nombre de paramètres aux seuls paramètres déterminants, on réécrit les équations sous forme adimensionnée en posant τ = βN×t. Les populations deviennent alors :
uc=nc/N
φk=nk/Nk
π=h/H
uν=hν/N
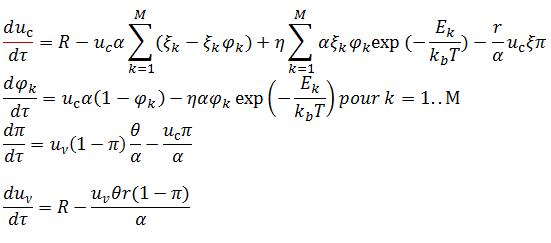
Les paramètres déterminants intervenant dans les équations sont :

Ce qui nous donne 2M+7 paramètres que l’on peut faire varier (si les α sont différents pour chaque piège on obtient 3M+7 paramètres). Par exemple, pour notre modèle, si on prend quatre pièges (M = 4) on obtient 15 paramètres inconnus (19 paramètres si les α sont différenciés). C’est en cela que la modélisation est complexe car il y a plus de paramètres ajustables que d'équations (ce qui laisse augurer la non unicité des ajustements).
