Le but principal de cette expèrience était de trouver un modéle mathématique à l'aide des réseaux complexes décrivant la dynamique d'un troupeau de moutons. Cependant nous ne sommes pas allés plus loin (lire notre projet proposé en téléchargement dans le menu).
L'analogie entre un réseau métrique et un réseau ER
Un réseau à topologie métrique n'est rien d'autre qu'un réseau ER de par sa définition. C'est à dire qu' on aura un lien si deux individus sont assez proches. De ce fait si on suppose l'intéraction de nos moutons métrique alors on suppose qu'il peut y avoir un réseau ER caché dérrière.
Supposons equi-probabilité de trouver un mouton sur un espace donné. On cherche maintenant quelle est la probabilité qu'un mouton soit connecté à un ou plusieurs autre(s) mouton(s) sachant qu'il a une portée d'intéraction de R. Reformulé différament cela donnerait : quelle est la probabilité qu'il y ait n moutons dans une surface donnée sachant qu'un mouton s'y trouve. On reconnait tout de suite une loi binomiale.
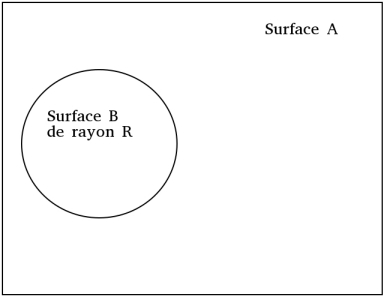
Par hypothèse on aura si on considére l'enclos ci-dessu :
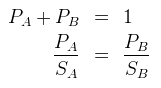
Pour N individus, le nombre n de moutons à porté d'interaction suit la distribution suivante si on néglige les effets de bords :
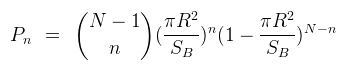
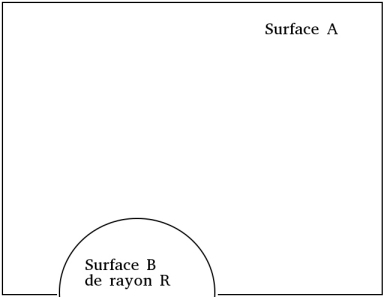
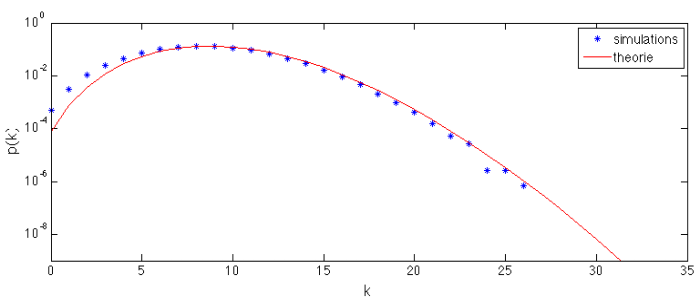
Effectivement la question de négliger les effets de bords apparait du moment où le rayon entre en jeu. Elle est importante puisque si l'on considére la figure suivante la probabilité d'être connecté à un autre mouton est beaucoup plus petite. C'est pourquoi nous avons tracés les courbes suivantes. Il s'agit d'une simulation où l'on dispose aléatoirement des points puis on les compte sur un disque de rayon R. On peut voir que malgrès les effets de bords la théorie est une très bonne approximation.
Par identification avec la loi de distribution de degrès d'ER on peut dire que :
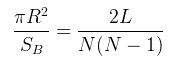
Si l'on revient à nos moutons de l'expérience on sait d'après notre étude que le réseau est percolé et presque fully connected donc :
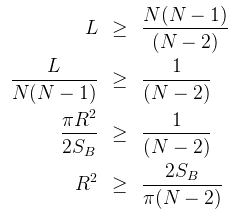
Le problème est que nous n'avons pas essayé la performance de ce modéle métrique nous ne pouvons rien conclure il nous aurait fallu plus de temps pour chercher ensuite la fonction de transmission.
L'analogie entre un réseau topologique et un réseau ER
Nous ne pouvons pas dire grand chose mise à part que les moutons ne suivent pas un simple modéle métrique mais bien un mélange des deux puisque suivant l'expérience l'intéraction topologique se rapproche plus de la réalité que la métrique(voir compte rendu).