La distribution de degrés

Nous l'avons tracées de 3 manières différentes :

Pour pouvoir faire nos calculs on fixe le nombre de noeuds du sytème et on définit que l'ajout d'un lien correspond à un pas de temps. C'est à dire que l'on définit "t=0" par le moment où seul les noeuds sont présents, puis à chaque pas de temps "t" on lie deux noeuds de notre réseau pris aléatoirement.

On posera pour la suite :

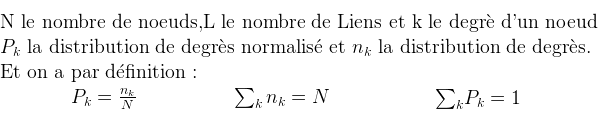
• Informatiquement :

  Nous avons tout simplement pris les résultats de l'étude d'introduction (la probabilité de connexion incorporé dans la loi binomiale) puis on l'a calulé informatiquement. Soit tracer :

  

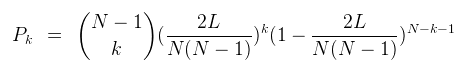
• Avec les simulations :

  Nous avons construit informatiquement le réseau et à chaque ajout de lien on observe la distribution de degrés, sa moyenne et son écart type.

• Analytiquement :

  Il s'agit de résoudre l'équation différentielle suivante, établie par récurrence, en prenant comme objet le nombre de noeuds de degrés k en fonction du temps. En effet la variation du nombre de noeuds de degrés k au temps t+1 est la combinaison linéaire du nombre de noeuds de degré k au temps t et du nombre de noeuds de degré k-1 au temps t. On comprends naturellement que à chaque pas de temps on connecte un lien qui modifie le degré de deux noeuds. Ainsi pour un degré k fixé il y a la possibilité de gagner un noeud si le lien se connecte sur un noeud de degré k-1 ou de perdre un noeud si le lien se connecte sur un noeud de degré k.

  

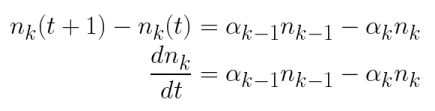
  On peut réécrire l'équation sous la forme d'une dérivée continue en faisant apparaitre le taux de variation pour un pas de temps t+dt avec dans notre cas dt =1.

  On suppose qu'il n'y a pas de "preferencial attachment", ce qui veut dire que la probabilité de connexion entre chaque noeud est identique on peut donc affirmer que :

  

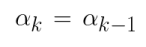
  On utilise ensuite la fonction génératrice définie par :

  

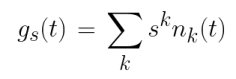
  Qui nous permet de réecrire la prémière equation sous une forme simple:

  

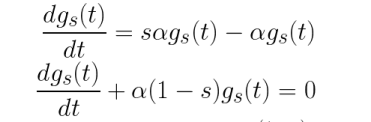
  Car on fait la somme sur tout les k de 1 à l'infini donc que c'est exactement pareil que de faire les sommes des k-1=1 à l'infini

  La solution est donnée par :

  

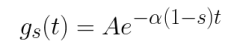
  avec A une constante

  On remonte à notre distribution de degrés :

  

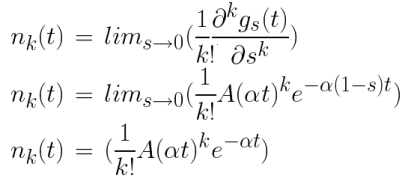
  Il nous suffit de déterminer nos constantes A et alpha avec nos conditions initiales qui viennent de la normalisation de la distribution :

  

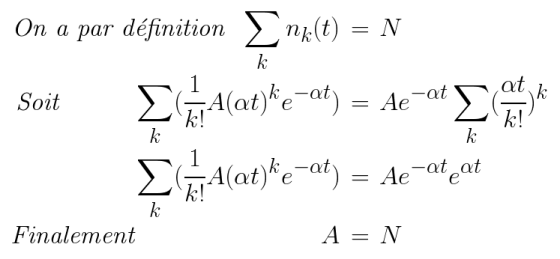
  Puis de la moyenne :

  

  Puisque notre t correspont finalement au nombre de liens présent dans notre système, soit t=L

  On peut conclure que :

  

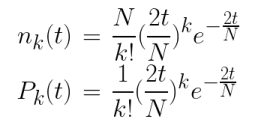
Une fois tout cela calculé on les a affiché sur un même graphe en faisant varier L le nombre de lien posé par courbe : (ODE = Analytiquement Binomial = Informatiquement Sim = Simulations)

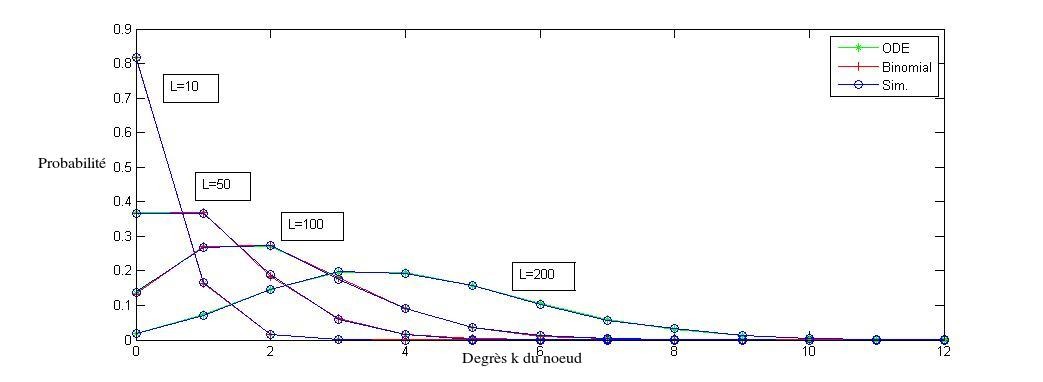
On remarque que la courbe s'applatit, le degré max augmente et ainsi la probabilité pour chaque degré diminue.