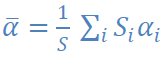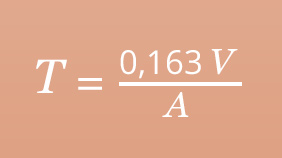LA RÉVERBÉRATION

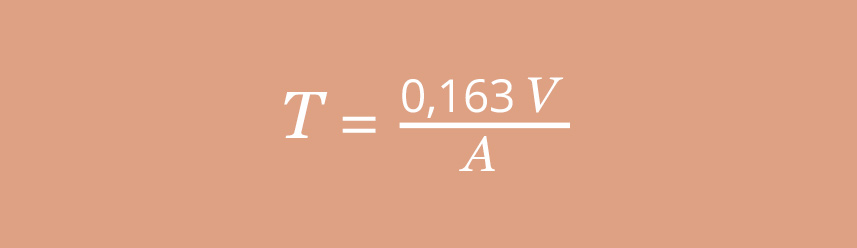
le son

Propagation en espace libre

Le son est la propagation d’ondes de pression dans un milieu matériel, en général l’air. Si l’on considère les ondes d’une source ponctuelle O placée dans un milieu homogène dont la propagation est isotrope, alors tous les points d’une sphère de rayon r sont atteints au même instant. Cette sphère est appelée surface d’onde, les points de celle-ci sont en phase et effectuent par conséquent la même vibration. On assimilera les surfaces d’onde à des plans lorsque l’on se placera à grande distance de la source, ces ondes seront considérées comme des ondes planes.
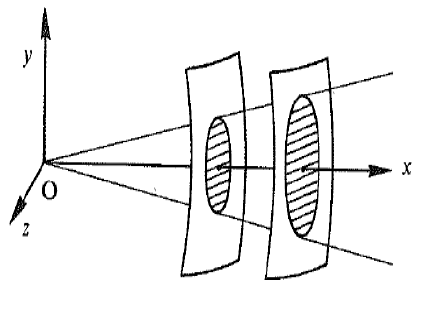figure 1 : Propagation d'une onde sphérique

L’énergie locale (ou densité d’énergie), si elle n’est pas absorbée dans le milieu, décroit étant donné que l’énergie de la surface totale d’onde se conserve. Comme la densité d’énergie d’une onde est proportionnelle au carré de son amplitude, on aura dans le cas d’une onde sphérique, une décroissance en 1/r². Le niveau de pression sonore (SPL) peut être calculé en un point par la formule suivante :
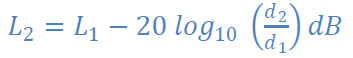L₁ niveau sonore à la distance d₁ de la source et L₂ celui à d₂

L’absorption par l’air doit être prise en compte lorsque l’on considère de grandes distances de propagation et pour des fréquences élevées. Cette absorption varie en fonction de la température, et est d’autant plus grande lorsque l’humidité ambiante est faible. On pourra dès lors noter que dans nos expériences, la salle possède des dimensions suffisamment petites pour que l’atténuation provoquée par l’air puisse être considérée comme négligeable devant celle induite par chaque réflexion sur les différentes surfaces.
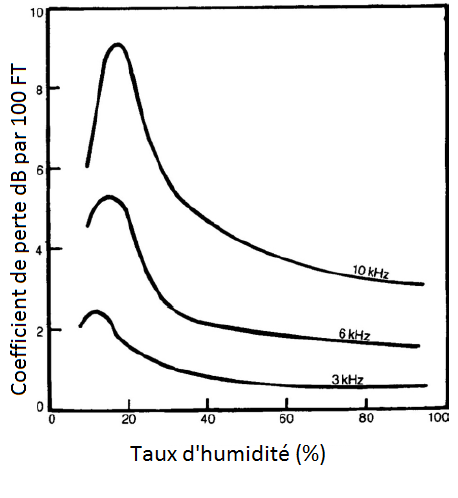figure 2 : Absorpsion par l'air en fontion de la distance et de l'humidité ambiante

Réflexion – Réfraction d’ondes sonores

Avant de discuter des propriétés des champs sonores en espaces clos, considérons d’abord le processus qui est fondamental pour leur présence : la réflexion d’une onde sonore plane par un seul mur ou surface. Si l’on considère un mur infini, le problème est grandement simplifié, on a une réflexion de type spéculaire dont l’angle incident de l’onde plane est égal à l’angle de réflexion de celle-ci. On appelle ce modèle, le modèle géométrique (ou acoustique des rayons).
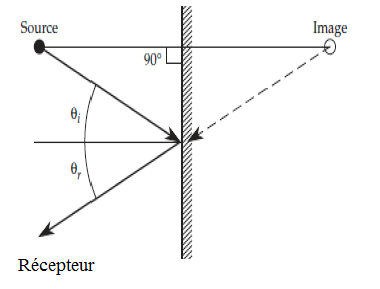figure 3 : Réflexion simple selon les lois de Descartes

Si l’on considère une salle parallélépipédique, une source sonore possède alors 6 sources images primaires. Les images des images conduisent alors à un nombre infini d’images. Le son mesuré en un point sera donc la résultante du son direct provenant de la source et des contributions de toutes les images de celle-ci. Pour des temps suffisamment longs, on pourra utiliser une approche statistique de la réponse acoustique de la salle.

Ce modèle reste cependant très limité. En effet la bande passante d’ondes sonores audibles est de 20Hz à 20KHz soit des longueurs d’ondes variant de 1.7cm à 17m.

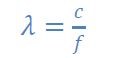c = 340 m/s vitesse du son dans l’air)

Il est fréquent d’avoir une géométrie de salle qui présente des irrégularités sur des échelles couvrant toute cette gamme de longueur (par exemple quand une onde sonore « frappe » la tête d’un auditeur ou une irrégularité murale comme sur le schéma ci-dessous). Il s’agit d’un modèle ondulatoire, plus adapté aux basses fréquences, où les ondes sonores seront diffractées lors des réflexions.

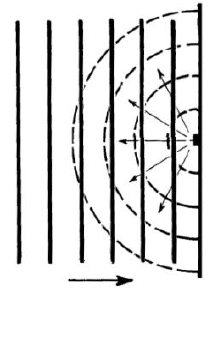figure 4 : Diffraction par une irrégularité murale

Effets de la réflexion-réfraction

A chaque réflexion, une onde sonore perd en intensité car le mur ou un obstacle absorbe une partie de son énergie. On peut illustrer cette perte comme la transmission d’une partie de l’amplitude de l’onde à travers le mur : l’amplitude de l’onde incidente étant la somme de celle réfléchie et de celle transmise.

La réverbération

Une résonance individuelle, lorsqu’on cesse de l’entretenir, en coupant la source, voit son énergie décroître exponentiellement au cours du temps.

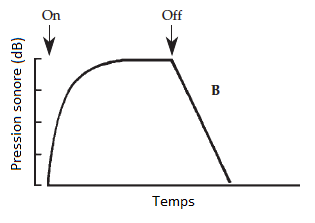figure 5 : Décroissance exponentielle après extinction de la source
Le temps de réverbération T (RT60) fut introduit au début du XXe siècle par W. C. Sabine, fondateur de l’acoustique architecturale comme la durée au bout de laquelle le niveau sonore a chuté de 60 décibels après extinction de la source.

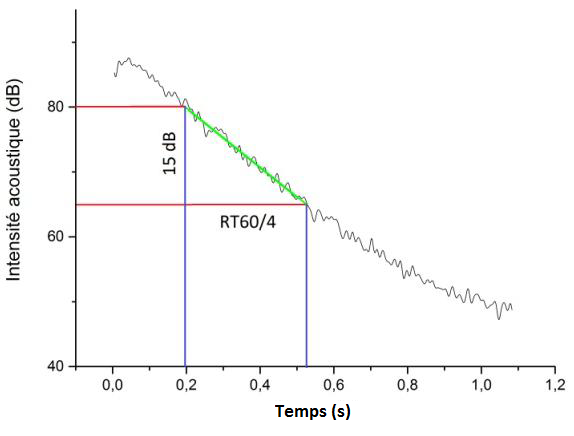figure 6 : Exemple de mesure du RT60
Il est intéressant de remarquer sur la courbe ci-dessus que la décroissance n’est plus exponentielle à partir de 0,6 s. Il s’agit de la contribution des modes basse fréquences de la salle dont le temps de réverbération est plus important que celui du reste des modes.

Ondes stationnaires – les modes d’une salle

Lorsque l’on considère la réflexion entre deux murs parallèles, on peut noter l’apparition d'ondes stationnaires. En effet, on aura alors un système résonant pour des fréquences multiples de la fondamentale :
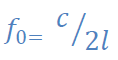l la distance séparant les murs
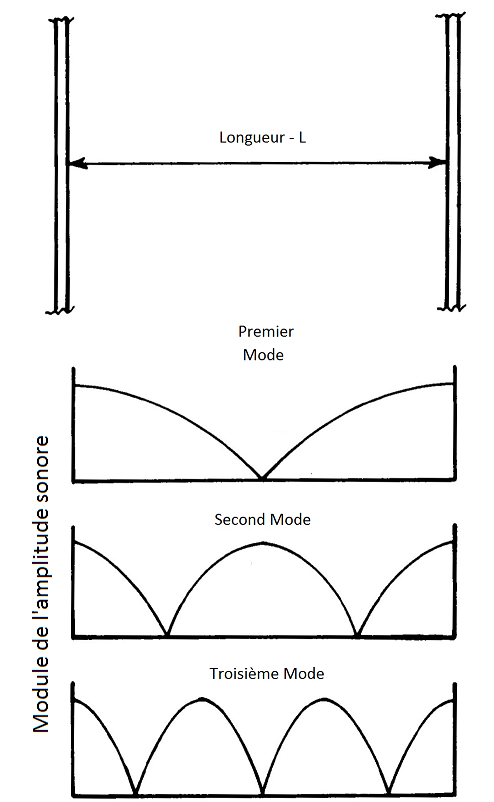figure 7 : Ondes stationnaires entre deux murs parallèles
En trois dimensions, dans une pièce parallélépipédique, on pourra observer des modes axiaux (entre deux murs), tangentiels (dans un plan parallèle à un mur) et obliques (faisant intervenir une trajectoire quelconque).
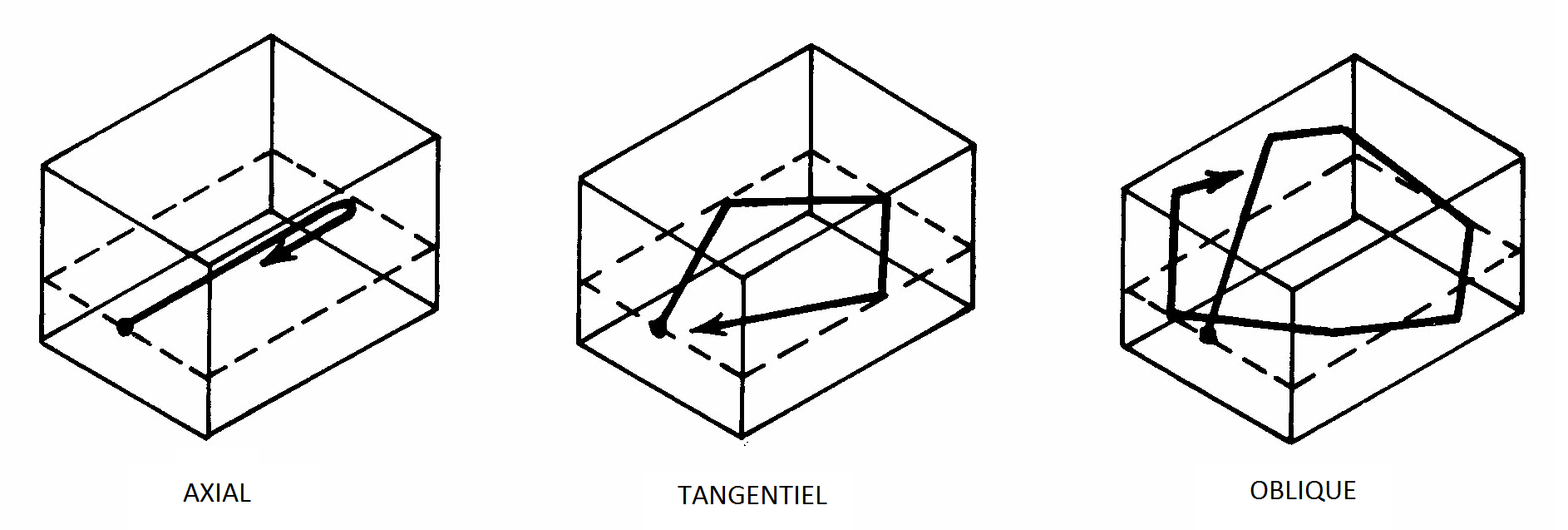figure 8 : Différents types de modes

On peut prédire les fréquences modales d'une pièce parallélépipédique (de dimensions L=6,8m W=5,7m et H=3,3m) grâce à la formule suivante :
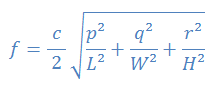c=340m/s la vitesse du son.
Les coefficients p,q,r (entiers positifs ou nuls) nous renseignent sur la nature du mode :
- si deux de ces coefficients sont nuls : mode axial
- si l'un de ces coefficients est nul : mode tangenciel
- si les trois sont non nuls : mode oblique

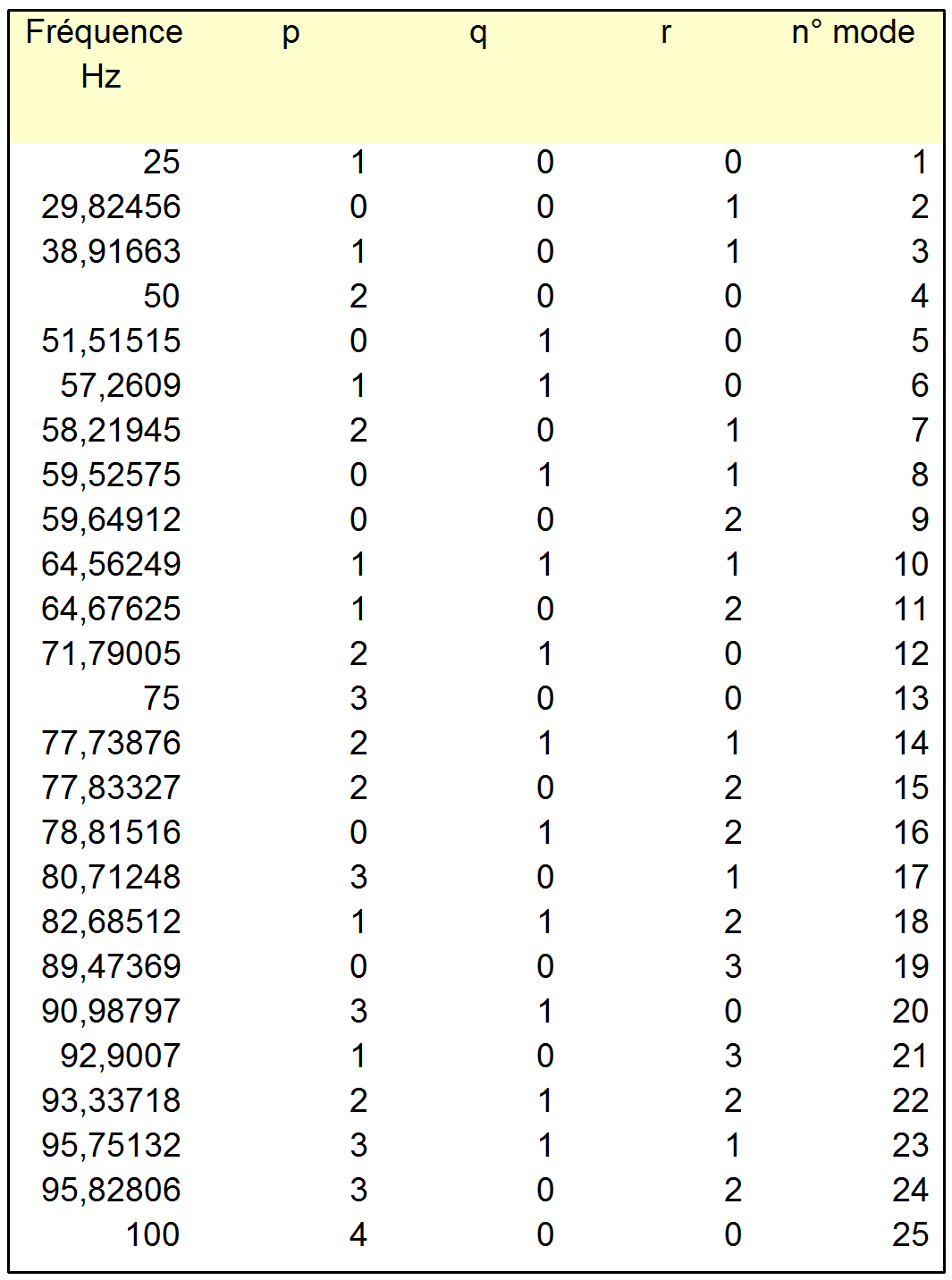figure 9 : 25 premiers modes d'une pièce parallélépipédique

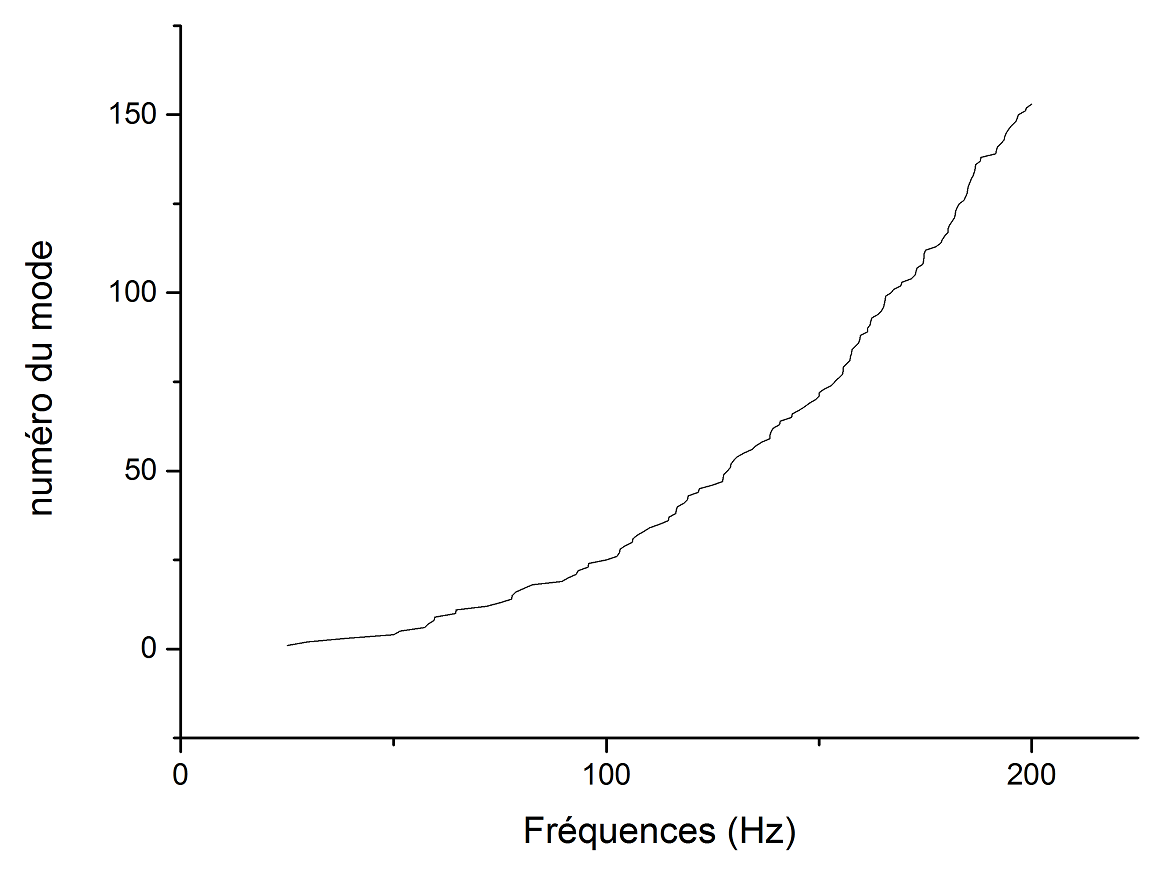figure 10 : Illustration de la densité modale cumulée en fonction de la fréquence
On peut noter que la densité modale cumulée augmente exponentiellement avec la fréquence.

Lorsque l'on mesure le temps de réverbération avec des signaux purs à basse fréquence, on met en évidence des temps de réverbération longs aux fréquences modales. Ces pics sont caractéristiques des premiers modes et ne sont pas représentatifs de la salle considérée comme un tout. Une densité modale élevée (à haute fréquence), qui permet une distribution uniforme de l’énergie sonore, est nécessaire pour appliquer les équations de la réverbération d’origine statistique (loi d'Eyring-Norris et loi de Sabine).
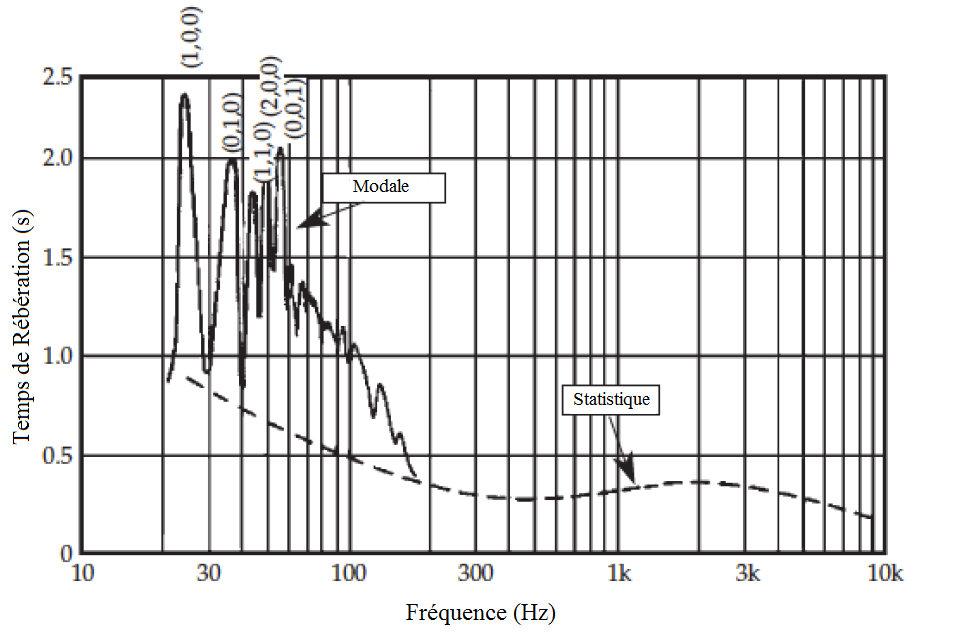figure 11 : RT60 en fonction de la fréquence stimulée d'après Beranek et Schultz
Les premiers modes d’une pièce (modes axiaux et tangenciels de basses fréquences) ont une décroissance plus lente que les autres modes, et prédominent sur ces derniers en fin de réverbération.

Quantitativement, on définit la bande passante Δf par l'intervale fréquenciel centré sur la résonance séparant les fréquences où l'intensité sonore est à -3dB de celle du maximum.
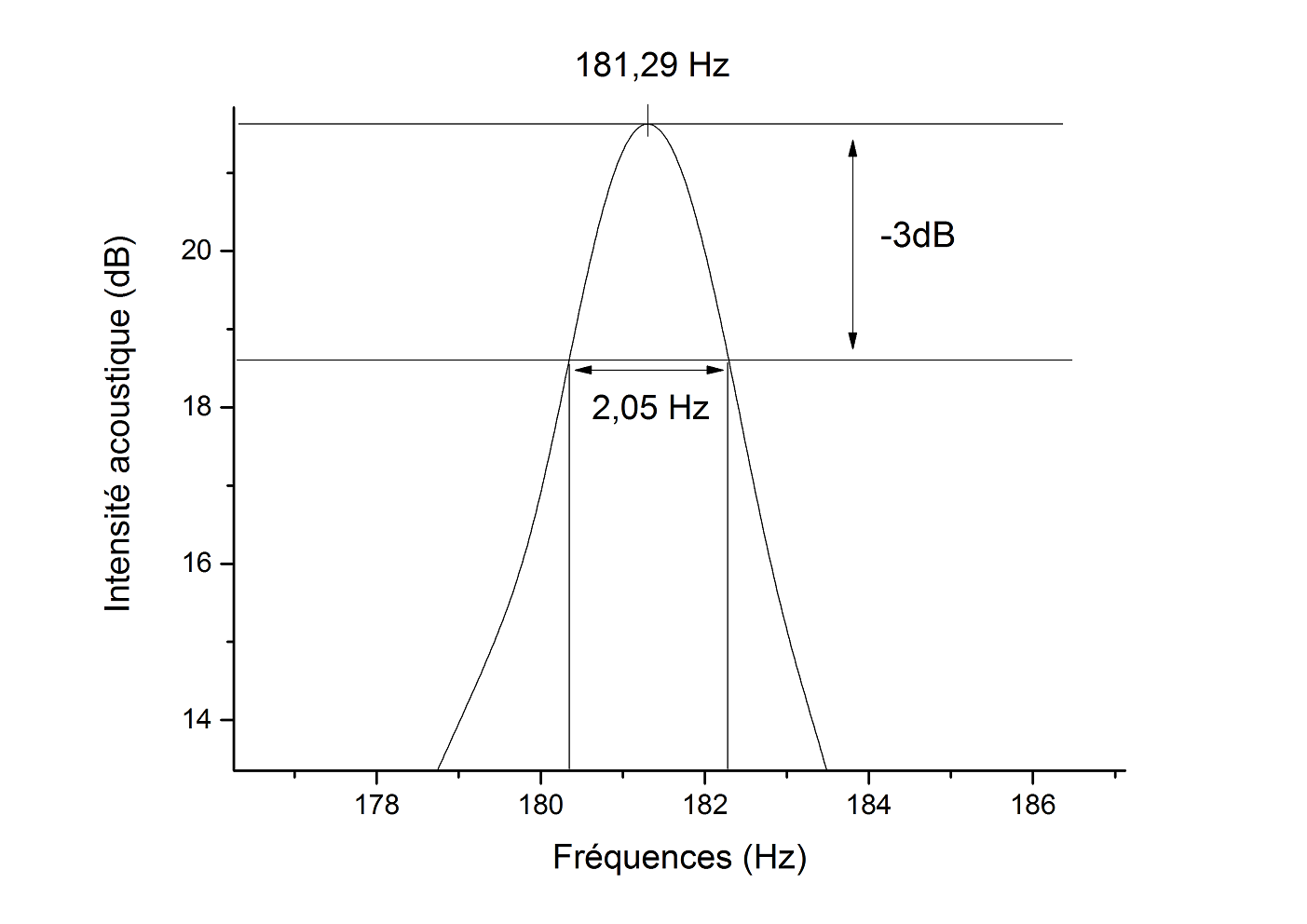figure 12 : Mesure du RT60 par la largeur modale à -3dB
Relation entre temps de réverbération T (RT60) et largeur de résonance Δf :

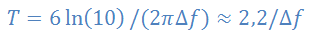
Loi d’Eyring-Norris et loi de Sabine

Considérons qu’après chaque réflexion sur un mur, un rayon est atténué par un facteur (1- α) où α est le coefficient d’absorption. On considère de manière statistique qu’un front d’onde parcourt en moyenne la distance l entre deux réflexions consécutives. On estime l grâce à la formule suivante :

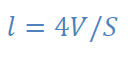V volume en m3 et S surface en m²
(cette formule à été vérifiée par simulation numérique de rayons aléatoires en espace clos durant le projet).
En effet le front d’onde initial, après quelques réflexions sera diffusé de manière aléatoire dans la salle, ainsi l’intensité d’une onde est réduite au bout du temps t d’un facteur :
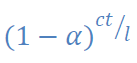c=340m/s la vitesse du son.
Donc l’énergie qui atteint un observateur dans la partie réverbérante du signal est donnée par :

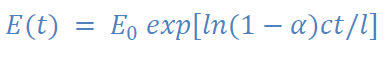
On pourra alors prédire le temps de réverbération grâce à la formule d’Eyring-Norris :
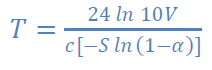Si α<<1 alors ln(1−α)≈−α

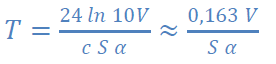
On aboutit alors à une forme simplifiée appelée loi de Sabine qui fut déterminée empiriquement lors des premières études de la réverbération. De nos jours cette formule reste très largement employée dès lors que l’hypothèse α<<1 est vérifiée.
Loi de Sabine :
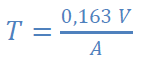V volume de la pièce et A aire effective d’absorption moyenne de la salle.

Aire effective d’absorption

On définit maintenant l’aire effective d’absorption :
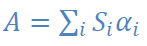i représente chaque élément absorbant de la pièce
Cette aire effective rend compte de l’absorption par toutes les surfaces de la salle. On peut aussi définir α le coefficient d’absorption moyen :