Avant toute expérience basé sur notre état, il faut s'assurer de la fidélité de cet état vis à vis de l'état théorique souhaité.
Pour cela nous allons reconstruire l'opérateur densité de notre système en procédant à la tomographie quantique de ce dernier.
Il devient nécessaire d'élargir le formalisme mathématique en introduisant l'opérateur densité lorsque l'on veut décrire des systèmes pour lesquels toutes les quantités physiques associées à un ensemble complet d'observables qui commutent (ECOC) n'ont pas été mesurées, ou lorsqu'une source peut générer différents types d'états (mixture statistique)
Le chapitre 2.1 s'attelle à démontrer que pour un système bipartite l'opérateur densité s'écrit :
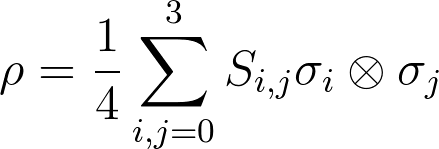
Nous effectuerons donc 16 mesures afin de reconstruire l'opérateur densité de notre état¹, que nous comparerons ensuite à l'opérateur théorique suivant :
Pour effectuer ces 16 mesures, nous utiliserons une lame demi-onde, une lame quart d'onde et un polariseur comme détaillé dans le chapitre 2.2.
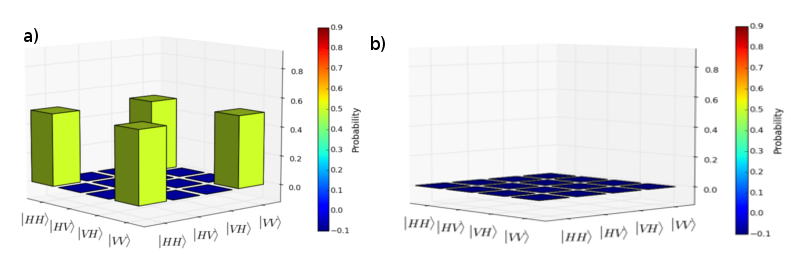
Nous pouvons donc reconstruire notre opérateur :
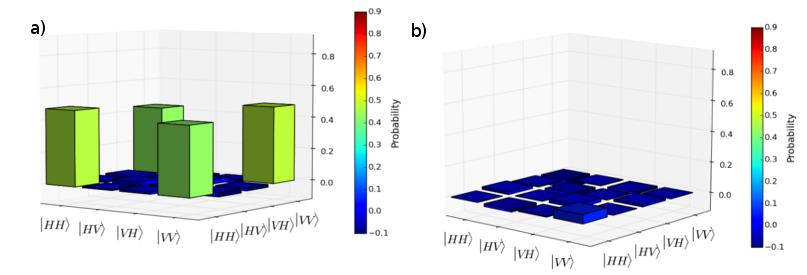
Nos mesures nous amènent à une fidélité de 95 %.
Les 5 % d'écart avec l'opérateur théorique sont dus à des erreurs d'alignement des différents instruments optiques. L'écart aux résultats théoriques s’expliquant
par la cohérence imparfaite de notre source laser, de possible
imperfections lors de l’alignement du dispositif, ainsi que de possible
erreurs d'orientation des lames à retard lors des mesures de
coïncidences. Les résultats obtenus restent toutefois en très bon accord
avec la théorie et attestent par conséquent de la qualité de notre
source de paires de photons.
¹ : http://research.physics.illinois.edu/QI/Photonics/papers/My%20Collection.Data/PDF/Measurement%20of%20qubits.pdf