IV) Obtention de l'indice négatif
Afin de définir ce qu'est l'indice négatif, nous allons nous intérésser à un matériau de propriétés fortement magnétiques. Il sera donc caractérisé par la perméabilité magnétique effective ![]() et par la permittivité électrique effective
et par la permittivité électrique effective ![]() . Nous considérons toutefois que
. Nous considérons toutefois que ![]() reste inchangée.
reste inchangée.
1) Champ magnétique résultant :
Dans l'approximation où les résonateurs composant notre matériau sont excités simultanément, nous pouvons assimiler notre matériau à une cellule contenant deux résonateurs couplés.
L'équivalent physique de notre matériau est un système de deux circuits RLC couplés par une inductance mutuelle M, tous deux portés au potentiel électrique Ve de l'onde incidente.
Nous pouvons, d'après les lois des noeuds et des mailles, obtenir les courants ![]() et
et ![]() des deux circuits respectifs.
des deux circuits respectifs.
Avec le calcul du potentiel vecteur ![]() et la relation
et la relation ![]() , nous obtenons le champ magnétique
, nous obtenons le champ magnétique ![]() ainsi que le champ électrique
ainsi que le champ électrique ![]() avec l'équation de Maxwell Ampère
avec l'équation de Maxwell Ampère ![]() .
.
Dans la base sphérique, nous avons:
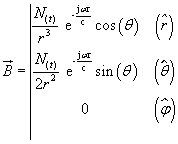 avec
avec
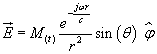 avec
avec 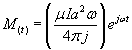
avec :
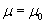 la perméabilité magnétique du vide,
la perméabilité magnétique du vide, - I=i1 le courant dans le circuit 1,
- a est le rayon d'une boucle de courant,
- ω est la fréquence de l'onde incidente,
- r est la distance au centre des boucles,
- c est la vitesse de la lumière,
- θ est l'angle de nutation,
- t le temps,
- j le nombre imaginaire.
Ces équations sont obtenues avec les approximations suivantes :
car nous faisons l'hypothèse d'une longueur d'onde lambda de l'ordre de 100 cm, d'un rayon a de l'ordre du millimètre et de la distance r de l'ordre du centimètre.
2) Un matériau homogène :
Afin de rendre homogène notre matériau, nous devons intégrer le champ magnétique à l'aide du théorème de Gauss et du théorème d'Ampère. Pour cela nous considérons un cube imaginaire d'arète 2d contenant nos deux résonateurs couplés.
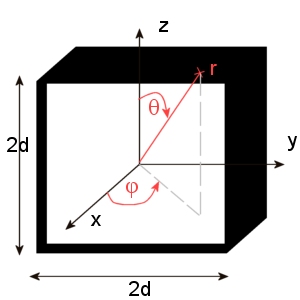
Cube imaginaire et repère sphérique
Le flux du champ magnétique nous est donné par le théorème de Gauss : ![]()
La circulation du champ magnétique nous est donnée par le théorème d'Ampère : ![]()
où ![]() est le champ créé par les résonateurs,
est le champ créé par les résonateurs, ![]() le champ magnétique de l'onde incidente,
le champ magnétique de l'onde incidente, ![]() et
et ![]() .
.
Nous pouvons relier ces deux grandeurs par un processus d'homogénéisation qui consiste à "moyenner" le flux et la circulation du champ magnétique, avec la relation ![]() :
:
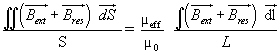
En intégrant le champ magnétique, nous obtenons : 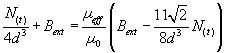 avec
avec ![]()
d'où ![]() avec
avec 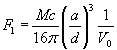 ,
, 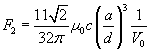 et
et 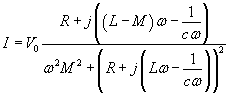 .
.
Nous obtenons donc une perméabilité magnétique relative ![]() en fonction de la pulsation ω de l'onde incidente, ce qui caractérise l'appellation "matériau dispersif".
en fonction de la pulsation ω de l'onde incidente, ce qui caractérise l'appellation "matériau dispersif".
Il est possible de séparer cette perméabilité en sa partie réelle et sa partie imaginaire.
Nous pouvons donc définir l'indice complexe du milieu : ![]() dont la partie réelle définit l'indice de réfraction et dont la partie imaginaire définit l'indice d'extinction.
dont la partie réelle définit l'indice de réfraction et dont la partie imaginaire définit l'indice d'extinction.