IV) L'innovation en optique
Dans le cadre de notre stage en licence de physique, nous avons élaboré un matériau virtuel afin d'en étudier les propriétés optiques. Ce dernier a été conçu par simulation numérique en langage C.
Notre matériau est assimilé à une simple interface sur laquelle nous envoyons une onde incidente excitatrice considérée comme plane.
A l'aide de ce modèle nous nous sommes focalisés sur l'étude de la réfraction et de la réflexion de l'onde incidente traversant le matériau dispersif, avec l'intention de mettre en évidence les effets de l'indice négatif.
1) L'onde excitatrice : Une onde plane
Nous envoyons une onde plane avec un angle d'incidence α sur notre matériau. Cette onde est caractérisée par le trièdre direct que forment son vecteur d'onde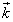 
, son champ électrique 
et son champ magnétique 
.
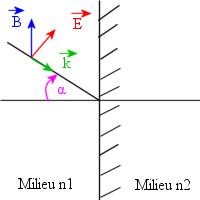
Champs magnétique et électrique quelconque à l'interface
Nous avons considéré les deux états particuliers suivants :
et 
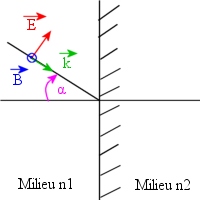
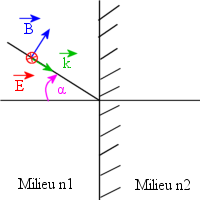
tangent à l'interface (cas 1) et tangent à l'interface (cas 2)
Un état quelconque de l'onde étant compris entre ces deux états.
2) Réflexion et réfraction de l'onde :
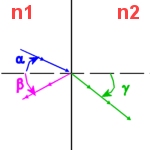
En utilisant les relations de continuité du champ dans le cas où il n'y pas de courant et de charges à l'interface, nous obtenons l'angle de réflexion β(ω) et l'angle de réfraction γ(ω), en fonction de la fréquence ω de l'onde, dans les deux cas précédents.
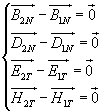avec 
et 
Relations de continuités
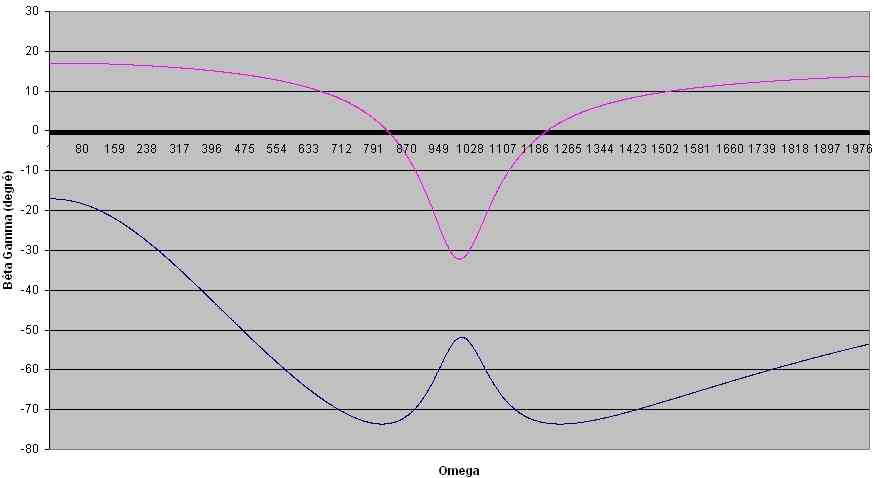
L'angle de réflexion β et l'angle de réfraction γ dans le cas 1
et le graphe de β(ω) et γ(ω) en fonction de ω pour ω0=10 et α=20°
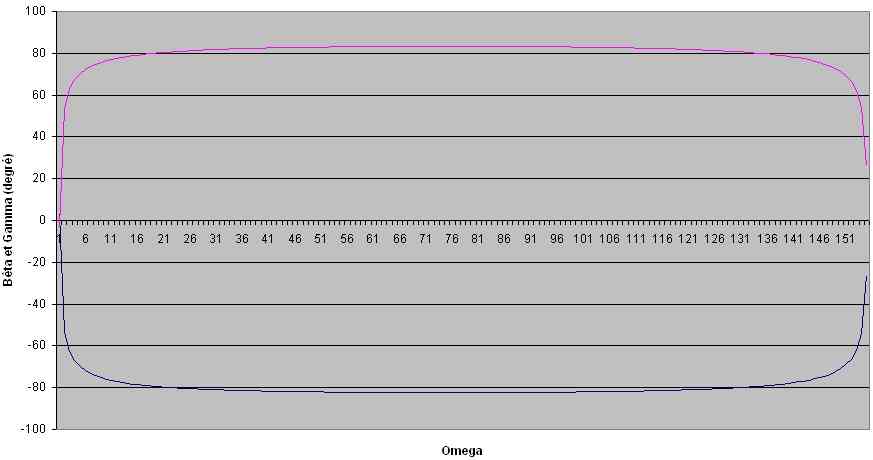
L'angle de réflexion β et l'angle de réfraction γ dans le cas 2
le graphe de β(ω) et γ(ω) en fonction de ω pour ω0=10 et α=20°
Nous pouvons constater d'après les courbes de β(ω) et γ(ω) en fonction de ω que ces angles varient fortement autour de la résonance, avec l'étonnante particularité d'être négatifs à la résonance pour γ l'angle de réfraction.
3) Les lois de Snell-Descartes remises en cause ? :
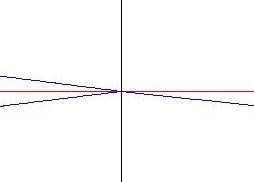
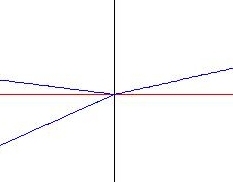
A l'aide de notre programme nous pouvons tracer les rayons : incident, réfléchie et réfracté en fonction de la fréquence de l'onde.
(a) |
(b) |
|---|---|
|
|
Nous pouvons constater qu'à l'interface les lois de Snell-Descartes traditionnelles s'appliquent lorsqu'on est loin de la résonance : graphe (a). Cependant, aux alentours de la résonance nous obtenons un angle de réfraction négatif, ce qui montre le caractère atypique de notre matériau : graphe (b).
(a) |
(b) |
|---|---|
|
|
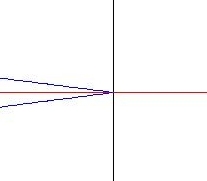
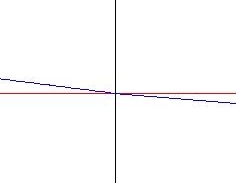
Loin de la résonance : graphe (a), l'onde est totalement réfléchie, c'est-à-dire que le métamatériau se comporte comme un miroir. Si nous nous plaçons proche de la résonance : graphe (b), dans une certaine borne de fréquence nous avons une transmission "habituelle". Ainsi, en ne laissant passer l'onde que pour certaines fréquences, notre matériau se comporte comme un filtre en fréquence.
4) Conclusion :
Rappellons les lois de Snell-Descartes à la traversée d'une interface par un rayon lumineux :
Traversée d'une interface entre le milieu n1 et le milieu n2. |
Loi de Snell-Descartes. |
|---|---|
 |
La validité des lois de Snell-Descartes impose que pour une réfraction négative nous devons avoir un indice négatif pour notre matériau. En effet le terme de gauche de l'équation étant positif et l'angle de réfraction gamma étant négatif, la seule manière de vérifier l'équation est d'avoir l'indice n2 de notre matériau négatif.