Nous n'avons pas de problèmes ici pour interpoler les données : le calcul est très rapide et on vérifie facilement si les conditions limites sont vérifiées.
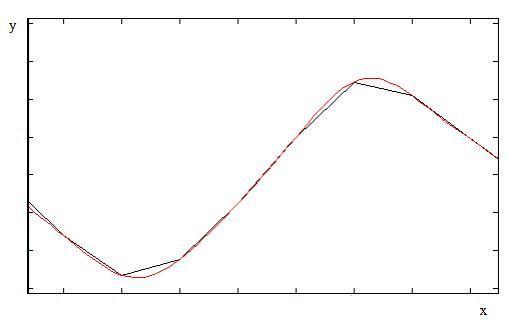
Interpolation d'une fonction unidimensionelle :
en noir, la fonction d'origine et en rouge la fonction interpolée
les points ont été reliés mais on en a en réalité un nombre discret
On voit bien ici que le théorème fonctionne correctement et que l'on peut réelement augmenter le nombre de points et donc la résolution.
Nous pouvons également réaliser la même opération sur une fonction bidimensionnelle, c'est justement ce qui nous interesse car nous avons la valeur du champ de spekle en fonction de l'absisse et de l'ordonnée. Remarquons que le champ de spekle est un champ à valeurs complexes, cependant, cela ne pose pas de problèmes pour l'interpolation : il suffit d'interpoler séparément la partie réelle et la partie imaginnaire. Voyons tout de suite le résultat que l'on parvient à obtenir avant de parler des différents problèmes rencontrés :
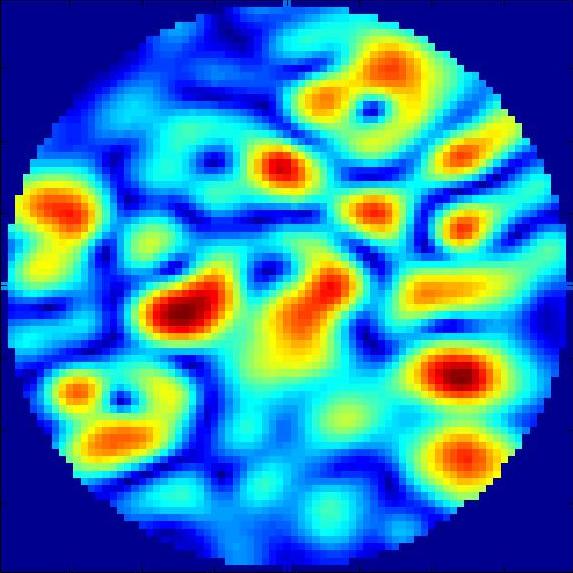

module du champ observé pour une fréquence donnée
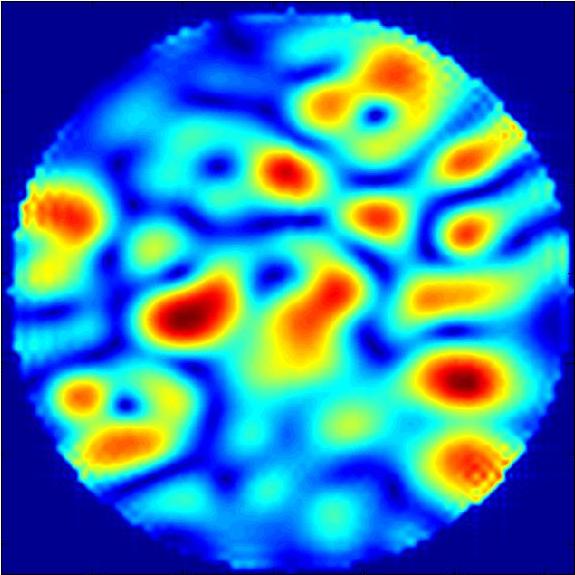

interpolation du même module du champ
La résolution a ici été multipliée par 8
Ici encore, le théorème semble fonctionner correctement : la résolution a bien été augmentée et on retrouve bien l'image d'origine. Cependant, on remarque l'existence de problèmes sur les bords de l'image : on observe l'apparition d'un signal ondulatoire parasite qui vient se superposer à l'image. Ce signal est généré l'absence de valeurs au delà des bords : une zone où la fonction n'est pas définie est équivalente à une zone où la fonction est nulle. Cela créé une sorte de discontinuité de la fonction. C'est pour attenuer cette discontinuité que l'on voit apparaître un signal parasite.
Nous allons cependant nous interesser à la phase du champ spekle ( et plus particulièrement aux singularités de phases et, par chance, la phase semble être moins sensible aux effets de bords liés à l'interpolation, comme en témoignent ces deux images correspondant à la phase des champs visibles ci-dessus :
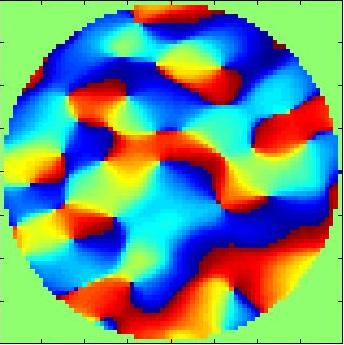
phase du champ observé pour une fréquence donnée


interpolation de la même phase du champ
La résolution a ici été multipliée par 8
Cependant, il nous est totalement impossible d'interpoler directement la fonction de phase du champ car celle-ci présente des discontinuités évidentes. Nous interpolons donc séparément partie réelle et partie imaginaire avant de reconstituer la fonction et d'en calculer la phase.
Un autre problème vient du fait que réaliser une interpolation d'une fonction bidimentionelle prend beaucoup plus de temps que pour une fonction unidimensionelle : environs quelques secondes pour la deuxième contre plusieurs minutes à plusieurs heures pour la première. Nous avons donc envisagé d'interpoler les fnctions bidimentionelles comme des fonctions unidimentionelles en commençant par exemple à interpoler uniquement les lignes puis en interpolant sur les colonnes mais de telles opérations ne permettent pas de retrouver l'ensemble des points du signal, comme en témoigne le shéma ci-dessous :
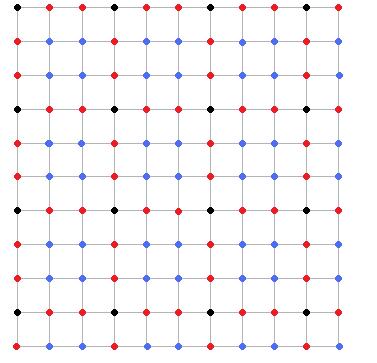
Les points noirs représentent les valeurs connues de la fonction. Les points rouges sont les points que l'on peut obtenir en interpolant en ligne. Les points bleus sont ceux qui ne sont pas calculables en interpolant en ligne : en effet, leurs lignes ne contiennent aucun points connus.
Nous n'avons donc pas d'autre solution pour améliorer la résolution que d'utiliser l'interpolation bidimensionelle malgré son coût en temps. Cependant, pour nous approcher d'une singularité afin d'en identifier les propriétés, nous ne sommes pas oligés d'interpoler toute la fonction de champ de départ mais nous pouvons prendre une zone plus petite comme nous le verrons un peu plus loin.