Modes de vibration d'un violon
Voici quelques notions théoriques nécessaires pour comprendre le phénomène de vibration.
Ondes Stationnaires :
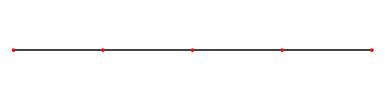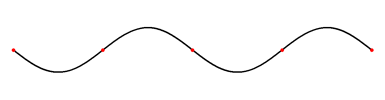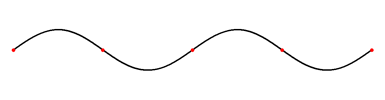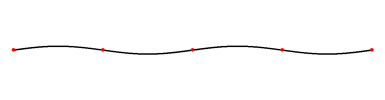
Propagation d’une onde dans une corde
Les points rouges sont appelés nœuds, ils sont immobiles.
La formation d'onde stationnaire est provoquée par l'interaction de plusieurs ondes de même fréquence. Lorsqu'une onde sinusoïdale périodique est introduite dans un système, ici une plaque de bois, celle-ci se réfléchie à ces extrémités et entraîne ainsi la superposition des ondes incidentes et des ondes réfléchies. Dans les conditions de stationnarité, c'est à dire, si ces ondes sont synchrones, on crée alors une onde stationnaire.
Cette condition est vérifiée si chaque onde se trouve dans le même état vibratoire après un aller retour le long de la corde, soit 2L = n λ
(n entier)
Une onde stationnaire forme alors des régions de grandes vibrations et des régions de très faibles vibrations. On les appelle les noeuds (en 1D), ou les lignes nodales (2D), et les ventres. « n » défini alors le nombre de noeuds de l'onde stationnaire. Le système noeuds – ventres définit les modes et vibre à la fréquence dite fréquence de résonance. Ils sont indicés par l'entier n ({1,2,...}). Le premier mode est appelé le mode fondamental, les autres sont les harmoniques.
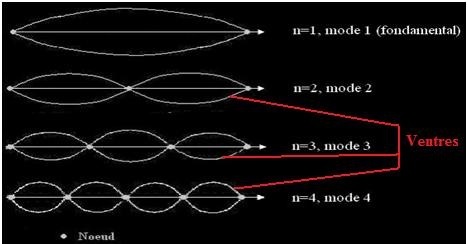
Modes, Nœuds et Ventres :
On définit une onde plane monochromatique, on considère le cas où l’onde se propage dans un milieu jusqu'à un de ses bords. Une partie de l’onde est alors transmise vers l'extérieur et le reste réfléchi. Mathématiquement, cette superposition s'écrit :
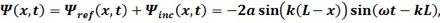
On définit l'amplitude en fonction de la position, A(x) = -2a.sin (k.(L-x)) où A(x) est indépendant du temps
Les points tels que A(x) = 0 sont appelés nœuds, ils correspondent aux minimums de vibrations, ils sont quasiment fixes.
Si A(x) = 2.a.sin(k.(L-x)) = 0 ( pour k.(L-x) = n.π
(n entier)) alors x= L-n. λ
/2.
Les points où |A(x)| = max (k.(L-x)=π
/2 {2π
}), donc x = L – (n+1/2).λ
/2, sont appelés ventres, ils correspondent aux maximum de vibrations et donc, de mouvement et oscillent entre -2a et 2a.
Propagation des ondes :
Pour expliquer le phénomène de propagation d'une onde et la démarche qui mène à la compréhension de ce système complexe, commençons par un exemple simple, le cas d'une corde tendue.
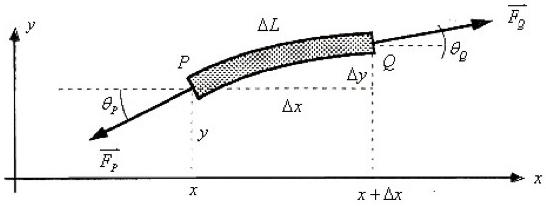
Soit une corde de longueur L tendue sous les forces de tension Fp et Fg (avec Fg=-Fp) et de masse linéique constante (μ
) le long du fil. On néglige ici la gravité.
Prenons un petit élément Δ
L, de masse Δ
m, on peut considérer le mouvement d’une petite partie de la longueur de la corde au cours du temps. Dans le cas d’un système avec de petits angles :
Bilan des forces :
Suivant y :
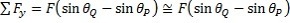
On retrouve la seconde loi de Newton : Δ
m = μ
Δ
x.
Ce qui nous donne :
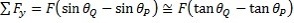
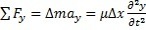
Or tan θ
g = (∂
y/∂
x)Q et tanθ
p = (∂
y/∂
x)p et en prenant la limite de Δ
x à l'infini,.
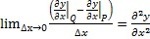
On obtient l'équation des cordes vibrantes (son équation de propagation) :
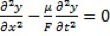
Mais une planche de bois n’est pas un milieu de propagation 1D aussi simple qu’une corde. Prenons à présent l'exemple des oscillations d'une poutre isotrope en flexion. Ce qui nous rajoute une dimension supplémentaire par rapport a la corde et donc nous rapproche un peu plus d’une plaque.
NB: Est nommé poutre tous les objets dont une des dimension est beaucoup plus grande que les deux autres.
L'équation fondamentale de la dynamique nous donne, pour un déplacement w(x,t) d'une poutre de surface S et de densité volumique ? sous l'action d’une force de torsion T :
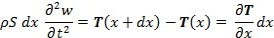
Si on définit
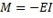
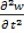
le moment de force, avec I le moment d'inertie de la poutre, on obtient :
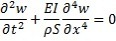
Pour utiliser cet exemple dans le cas non plus d’une poutre, mais d’une plaque, il faut considérer qu’il n’y a plus une seule dimension dominante mais deux.
Pour un violon cette étude étant trop complexe, (géométrie compliquée de l’instrument), nous avons préféré étudier des plaques de bois rectangulaires, qui sont une bonne approximation d’une plaque de violon (voir dans notre rapport
).
NB: Si l’on étend une des dimensions du modèle de la corde 1D à 2D, on obtient les équations d’une membrane.
Etude réalisée sur un tambour ici