|
|
Exploitation et interpretation
Nous avons recueilli 390 fichiers contenants le temps, les positions en x et y, ainsi que la température correspondant à chaque particule simulée.
Avec ces données, nous sommes donc capables de répondre à la question initialement posée: La force dipolaire est-elle le mécanisme dominant à l'origine de la fuite des particules hors du piège?
On peut déjà avoir un premier élément de réponse. En effet sur les 390 particules, seules 5 sont sorties au bout d'une seconde. Or expérimentalement, il est constaté qu'il ne reste que 50% des atomes au bout de 0.1 seconde. Donc on peut légitimement écarter cette hypothèse en ce qui concerne le chauffage prématuré.
Pour aller plus loin, nous pouvons tracer la température moyenne par particule pendant la simulation. La température est donnée grâce à la relation de thermodynamique statistique:
|
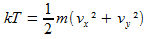
(1)
|
donc,
|
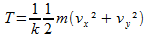
(2)
|
C'est en quelque sorte un abus de langage car nous ne somme pas à l'équilibre thermodynamique,
mais c'est simplement par commodité que nous effectuons cette transformation:
il est plus parlant d'utiliser des températures pour définir l'énergie des atomes.
Lorsqu'on trace, pour commencer, la température en fonction du temps pour une particule, on obtient ceci:
On se rend mieux compte de la structure du graphe lorsqu'on effectue un agrandissement:
Les plateaux caractérisent la température de la particule lorsque celle-ci évolue dans le centre du piège qui est quasi-plan.
Lorsque la particule est en interaction avec la barrière,
celle-ci gagne en température mais en perd de suite une partie: elle monte sur la barrière puis redescend.
Ce qui nous intéresse ici, c'est le bilan avant/après interaction.
Il est clair qu'on ne peut pas déterminer ici une tendance en ce qui concerne le chauffage en fonction du temps.
Pour ce faire, il faut prendre les parties du fichier où la particule est stable,
c'est-à-dire quand elle est au centre du piège, loin de la barrière de potentiel. De cette manière, nous étudions le système dans ce qui peut ressembler le plus à un état d'équilibre, hors interaction.
Nous devons maintenant traiter les fichiers correspondants à toutes les particules de la même manière,
de sorte à obtenir le graphe de la température par particule en fonction du temps.
A partir de ce moment là, un problème nous incombe.
En effet, la fonction ode15s incrémente le temps avec un pas variable qui dépend de l'évènement lui-même.
C'est à dire que les fichiers auront tous des pas de temps différents.
Nous devons donc trouver un moyen d'avoir une base de temps commune à tous les fichiers afin de pouvoir tracer ce graphe.
Nous utilisons donc une autre fonction présente dans MatLab, à savoir spline
qui effectue une interpolation des valeurs de la température sur un pas de temps que nous avons préalablement choisi.
Grâce à cela, nous sommes enfin capables de tracer ce graphe.
D'après le développement de Robin Kaiser (que nous ne redémontrerons pas ici),
nous devrions remarquer que la température dépend linéairement du temps:
avec 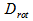 le coefficient de diffusion du laser en rotation.
Ce n'est pas tout à fait le cas; en effet nous constatons plutôt une allure exponentielle.
Nous pouvons le « fitter » avec une cubique pour avoir une idée de l'évolution de la température en fonction du temps.
Les 5 particules simulées qui sont sorties avaient à ce moment là en moyenne 1 mK (avec un écart-type de 0,3 mK).
Il ne nous reste qu'à résoudre: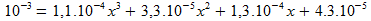 
La solution réelle est 1,78 seconde.
Donc a priori cela confirme le fait que la fluctuation de la force dipolaire n'est pas le facteur limitant dans la durée de la manipulation,
étant donné qu'il est observé que la moitié des particules fuit du piège au bout de 0.1 seconde.
Mais on ne doit pas le négliger puisqu'on a estimé à 1.78 seconde le temps de fuite moyen d'une particule.
Bien sûr,
c'est un résultat à prendre avec des pincettes car il faudrait réaliser cette simulation plus longtemps et en prenant en compte plus de particules.
Validité
Après avoir précédemment rencontré des problèmes à propos de la méthode d'intégration,
notamment en ce qui concerne la déviation numérique, une petite vérification ou estimation de la déviation s'impose d'elle même.
Nous devons vérifier si le chauffage que nous avons observé n'est pas un chauffage dû à une déviation numérique mais bien dû à la fluctuation de la force dipolaire.
Pour cela, nous allons simuler avec les même conditions initiales une particule dans un piège avec un potentiel fixe, puis dans le piège où le potentiel est tournant.
Nous comparerons ensuite le chauffage dans les deux expériences.
Conditions initiales:
Vx(0) = 0.05; où Vx(0) définit la vitesse initiale suivant la composante x.
x(0) = 2.0029.104; où x(0) définit la position initiale en abcisse.
Vy(0) = 0.02; où Vy(0) définit la vitesse initiale suivant la composante y.
y(0) = 2.5824.104; où y(0) définit la position initiale en ordonnée.
Graphe de la température en fonction du temps pour le potentiel rotatif
Graphe de la température en fonction du temps pour le potentiel fixe
Chauffage avec le potentiel fixe ~ 10-9 / 10-10 Kelvins
Chauffage avec le potentiel tournant ~ 10-4 Kelvins
La conclusion de cela est que le « chauffage numérique » est négligeable, devant celui résultant de la fluctuation de la force dipolaire.
Perspectives
Si nous parvenons à simuler plus longtemps un grand nombre particules, nous pourrions déterminer la loi qui régit la décroissance caractéristique des particules en fonction du temps et peut-être remarquer la présence de phénomènes inattendus comme un seuil...
|
|
.jpg)
ok.jpg)
