Comme expliqué précédemment, il est nécessaire d'augmenter la densité des atomes jusqu'à 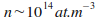 .
Pour y parvenir, la procédure consiste en la diminution du volume contenant les atomes.
Maheureusement, dans de telles conditions, les atomes gagnent en énergie cinétique et quittent le piège après un temps très court (moins d'une seconde).
Plusieurs hypothèses ont été émises pour la cause de ce problème : il est possible que les fluctuations au cours du temps de la force dipolaire en soient à l'origine.
Le but de notre stage est de répondre à la question « Les fluctuations de la force dipolaire sont-elles responsables de la fuite des atomes ? ».
Pour cela, nous devons mettre au point un modèle informatique permettant de simuler la dynamique du système considéré (atomes + piège) tout en ayant un total contrôle des paramètres physiques.
Si nous sommes capables de concevoir une simulation suffisamment « réaliste », nous pourrons alors répondre à la question posée.
Il existe plusieurs facteurs influant sur le comportement des atomes au sein du piège (la force de pression de radiation par exemple), comme nous nous intéressons qu'à seuls de ces derniers (la force dipolaire), nous ne simulerons que l'action de cette force sur les atomes.
Il n'est pas nécessaire de simuler tous les facteurs dans la même simulation pour observer les effets de l'un d'entre eux.
La démarche à suivre est la suivante : .
Pour y parvenir, la procédure consiste en la diminution du volume contenant les atomes.
Maheureusement, dans de telles conditions, les atomes gagnent en énergie cinétique et quittent le piège après un temps très court (moins d'une seconde).
Plusieurs hypothèses ont été émises pour la cause de ce problème : il est possible que les fluctuations au cours du temps de la force dipolaire en soient à l'origine.
Le but de notre stage est de répondre à la question « Les fluctuations de la force dipolaire sont-elles responsables de la fuite des atomes ? ».
Pour cela, nous devons mettre au point un modèle informatique permettant de simuler la dynamique du système considéré (atomes + piège) tout en ayant un total contrôle des paramètres physiques.
Si nous sommes capables de concevoir une simulation suffisamment « réaliste », nous pourrons alors répondre à la question posée.
Il existe plusieurs facteurs influant sur le comportement des atomes au sein du piège (la force de pression de radiation par exemple), comme nous nous intéressons qu'à seuls de ces derniers (la force dipolaire), nous ne simulerons que l'action de cette force sur les atomes.
Il n'est pas nécessaire de simuler tous les facteurs dans la même simulation pour observer les effets de l'un d'entre eux.
La démarche à suivre est la suivante :
- Nous simulons l'effet de la force dipolaire sur le comportement des atomes piégés.
- Nous quantifions le chauffage induit par cette force, c'est-à-dire l'augmentation de l'energie un après un temps d'au moins une seconde
- Il se présente alors deux cas de figure :
-
Soit les atomes gagnent suffisamment d'énergie cinétique pour quitter le piège après un temps semblable ou inférieur à celui obervé expérimentalement,
on en déduit alors que les fluctuations de la force dipolaire peuvent être responsables de la fuite prématurée des atomes.
-
Soit le temps de fuite des atomes est supérieur à celui observé expérimentalement,
on en déduit alors que les fluctuations de la force dipolaire ne sont probablement pas responsables de la fuite observée des atomes.
- Ces prédictions doivent être vérifiées expérimentalement (mais ce n'est pas le propos de notre projet)
Notre point de vue de la manipulation ne nécessite pas de considérer les interactions entre atomes, la simulation est donc effectuée atome par atome, puis les résultats individuels sont réunis afin de faire une satistique.
Puisque nous devons concevoir intégralement le programme de simulation, nous commençons par simuler le système de manière très simplifiée. Nous nous plaçons dans l'approximation de la force moyenne, dans la géométrie suivante : A deux dimensions, l'atome évolue sur un plan repéré par (xOy) et est piégé entre deux murs de potentiels. Le potentiel ressenti par l'atome s'écrit alors
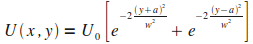
|
(1)
|
Avec 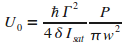
Pour se représenter la géométrie, on trace le graphe du potentiel.
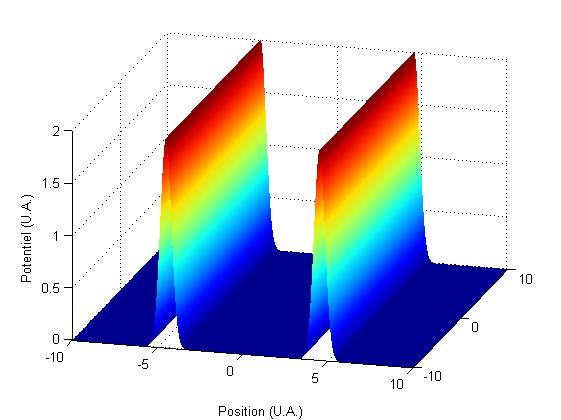
FIG. 1 - Potentiel rectiligne fixe
Pour simuler l'évolution temporelle de l'atome, il faut d'abord écrire ses équations du mouvement.
Pour cela on utilise le fait que la force subie par l'atome dérive du potentiel ressenti.
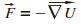
|
(2)
|
D'où l'expression explicite de la force dipolaire.
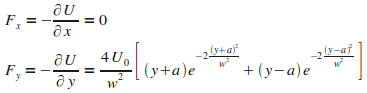
|
(3)
|
Toujours dans le but de représenter la situation considérée, on trace le graphe de la force subie par l'atome. On remarque que cette force dépend de la position de l'atome.
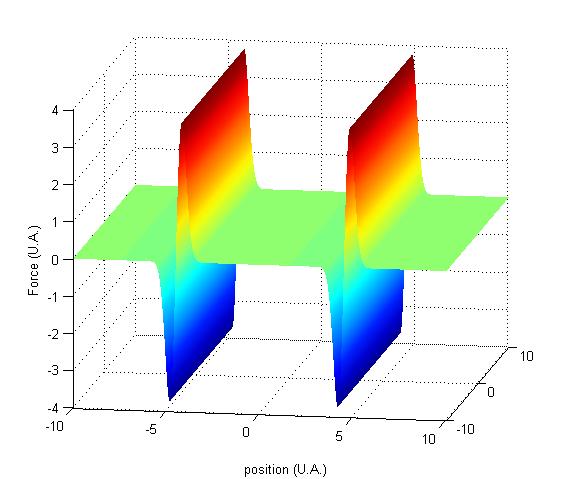
FIG. 2 - Force dipolaire dérivant du potentiel rectiligne fixe
On écrit ensuite la relation fondamentale de la dynamique,
afin d'obtenir les équations du mouvement de l'atome en x
et en y.
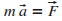
|
(4)
|
On décompose cette relation selon les deux composantes
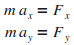
|
(5)
|
On en déduit les équations du mouvement.
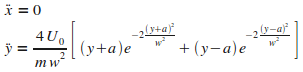
|
(6)
|
D'après ces équations, la particule subit une accélération selon la direction y,
dépendante de la composante y de sa position,
et ne subit aucune accélération selon x,
ce qui se comprend car le potentiel considéré ici est « rectiligne », parallèle à l'axe x, et situé en -a et a (cf. FIG. 1).
Maintenant que nous avons les équations du mouvement, il faut les résoudre.
Nous ne pouvons bien évidemment pas les résoudre analytiquement,
c'est pourquoi nous utilisons le logiciel MatLab,
afin de résoudre numériquement ces équations. Dans ce logiciel sont déjà implémentés des algotrithmes de résolution numérique.
Etant peu familiers avec l'utilisation de ces fonctions,
nous allons d'abord résoudre les équations différentielles par la « méthode d'Euler »
(il s'agit en fait d'un développement limité à l'ordre 1).
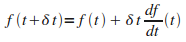
|
(7)
|
Les équations différentielles considérées sont d'ordre 2, la méthode d'Euler se fait donc en deux temps.
Il faut d'abord intégrer les accélérations 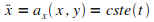 et
et 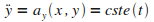 pour obtenir les vitesses
pour obtenir les vitesses 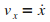 et
et 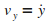 : :
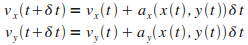
|
(8)
|
Puis intégrer ces vitesses pour obtenir les positions en fonction du temps
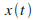 et et 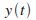 : :
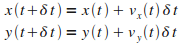
|
(9)
|
Pour appliquer cette méthode, nous devons connaître les conditions initiales 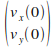 et et 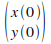 . Pour commencer nous choisissons ces conditions initiales arbitrairement, tout en restant raisonnables (c'est-à-dire que nous choisissons des positions telles que l'atome soit entre les deux barrières de potentiel, avec une vitesse de l'ordre du m/s). . Pour commencer nous choisissons ces conditions initiales arbitrairement, tout en restant raisonnables (c'est-à-dire que nous choisissons des positions telles que l'atome soit entre les deux barrières de potentiel, avec une vitesse de l'ordre du m/s).
L'algorithme d'Euler se déroule alors ainsi :
|
Initialisation
|
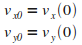
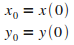
|
|
Itération n = 1
|
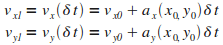
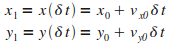
|
|
Itération n = 2
|
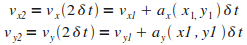
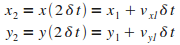
|
|
Itération n = 3
|
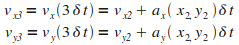
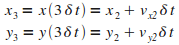
|
|
|

|
|
Itération n
|
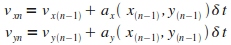
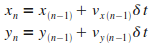
|
Il faut maintenant choisir un pas de simulation 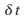 .
Pour cet essai, nous choisissons un pas arbitraire, relativement petit par rapport à la seconde,
de l'ordre de 100µs, dans le but d'avoir une résolution assez précise.
Maintenant, nous pouvons traduire cet algorithme en langage " MatLab ".
En le plaçant dans une boucle for,
on obtient alors la position .
Pour cet essai, nous choisissons un pas arbitraire, relativement petit par rapport à la seconde,
de l'ordre de 100µs, dans le but d'avoir une résolution assez précise.
Maintenant, nous pouvons traduire cet algorithme en langage " MatLab ".
En le plaçant dans une boucle for,
on obtient alors la position 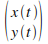 au cours du temps jusqu'à
au cours du temps jusqu'à 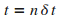 . .
Dans cette géométrie, l'accélération selon x est nulle,
on constate donc que la vitesse selon cette direction reste constante,
tandis que la vitesse selon y subit l'accélration
dans la direction y.
Pour observer le résultat, on trace la trajectoire de l'atome :
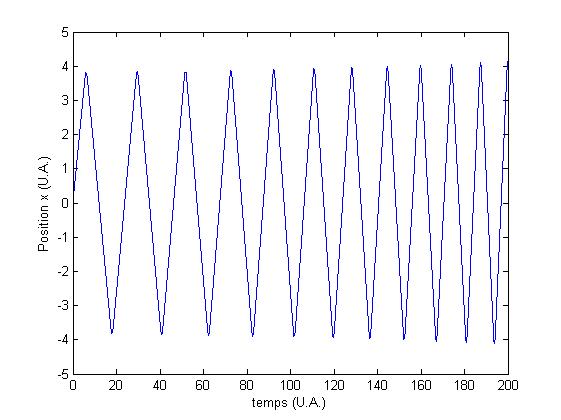
FIG. 3 - Trajectoire dans un potentiel rectiligne
Afin de se familiariser davantage avec l'utilisation de MatLab, nous effectuons la même simulation, avec une géométrie plus proche de la réalité de l'expérience. Nous sommes toujours à 2 Dimensions, dans l'approximation de la force moyenne, mais cette fois-ci l'atome est entouré d'un potentiel circulaire de rayon a.
Cette approximation peut se justifier ainsi : La fréquence de rotation des faisceaux lasers qui piègent l'atome (cf. rapport + introduction) est tellement élevée qu'ils forment une "cage" autour de l'atome, constante au cours du temps. Si l'atome ne se déplace que sur 2 dimensions, cette "cage" se modélise par un "mur" circulaire.
Le potentiel considéré s'exprime alors :
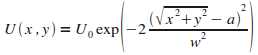
|
(10)
|
On trace son graphe :
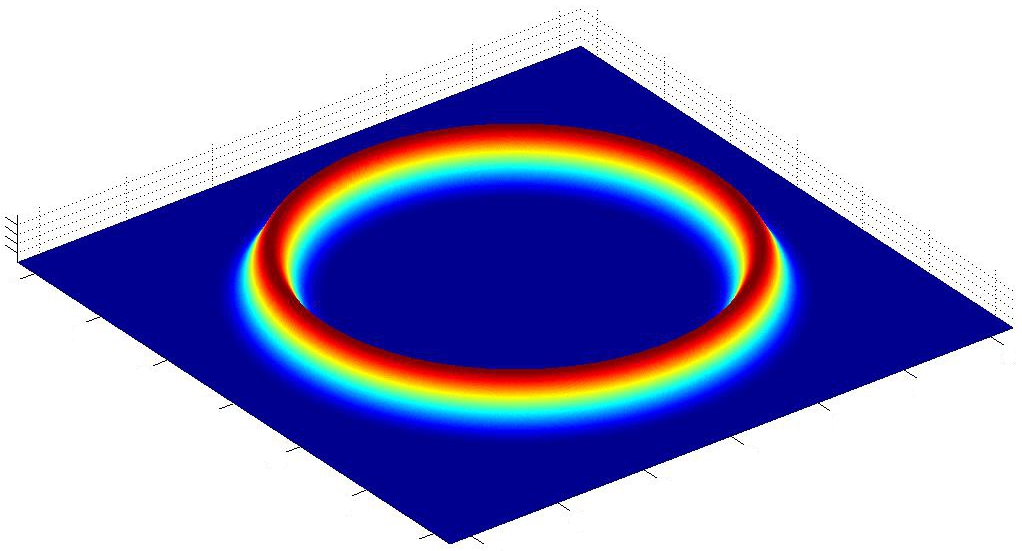
FIG. 4 - Potentiel circulaire fixe
En adoptant la même démarche que précédemment
(on exprime la force dipolaire avec le gradient du potentiel, puis on écrit le relation fondamentale de la dynamique),
on obtient les équations du mouvement (et donc les accélérations) :
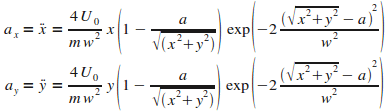
|
(11)
|
Maintenant que nous avons les accélérations selon x et y pour cette géométrie, nous procédons exactement de la même façon que pour la géométrie précédente, et nous obtenons donc la position de l'atome au cours du temps.
On peut alors tracer la trajectoire de l'atome
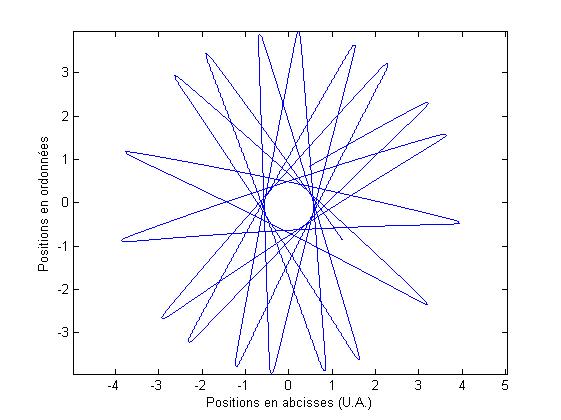
FIG. 5 - Trajectoire dans le piège circulaire fixe
D'après le potentiel que nous avons choisi, il semble que la trajectoire résolue numériquement soit correcte.
Nous sommes, pour l'instant, suffisamment familiers avec la résolution numérique d'équations différentielles,
nous allons donc nous intéresser à l'objet de notre stage.
Notre but est d'étudier l'effet des fluctuations de la force dipolaire.
Nous étudions le système physique à 2 dimensions, afin de simplifier le code de la simulation.
Il s'agit d'étudier l'interaction d'un atome avec un potentiel mais, cette fois-ci,
le potentiel considéré dépend du temps :
c'est une gaussienne à 2 dimensions en rotation à une fréquence
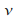 autour d'un point (que l'on choisit à l'origine du repère),
décrivant un cercle de rayon a.
Ce potentiel rotatif est la modélisation du faisceau laser oscillant permettant de piéger les atomes
(cf. rapport + introduction).
Si on fait une moyenne temporelle de ce potentiel tournant, on retrouve la configuration précédente,
avec un potentiel circulaire. autour d'un point (que l'on choisit à l'origine du repère),
décrivant un cercle de rayon a.
Ce potentiel rotatif est la modélisation du faisceau laser oscillant permettant de piéger les atomes
(cf. rapport + introduction).
Si on fait une moyenne temporelle de ce potentiel tournant, on retrouve la configuration précédente,
avec un potentiel circulaire.
L'expression du potentiel dépendant du temps est la suivante :
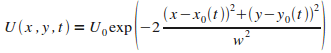
|
(12)
|
Avec
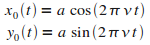
|
(13)
|
A un instant donné le potentiel ressemble alors à ça :
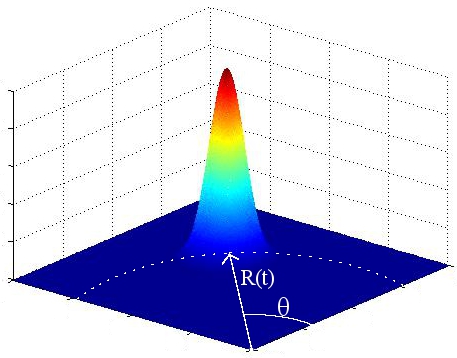
FIG. 6 - Potentiel circulaire tournant, à un instant donné
On procède de la même façon que précédemment pour écrire les équations du mouvement de l'atome dans cette configuration. On obtient :
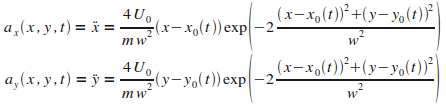
|
(14)
|
On remarque que, cette fois-ci, contrairement aux cas précédents,
les accélérations selons les deux composantes dépendent du temps.
Cela pose alors un nouveau problème :
le pas de simulation 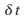 ne peut plus être choisi arbitrairement.
En effet, le potentiel est une gaussienne tournante à la vitesse angulaire ne peut plus être choisi arbitrairement.
En effet, le potentiel est une gaussienne tournante à la vitesse angulaire
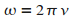 ,
pour simuler la manipulation de manière réaliste, le déplacement du potentiel au cours du temps doit être continu.
Autrement dit, entre deux itérations de la simulation, le potentiel ne doit pas faire de " saut ",
sans quoi l'atome pourrait intempestivement quitter le piège.
Pour réaliser cette condition, on choisit le pas de simulation tel que,
pendant ,
pour simuler la manipulation de manière réaliste, le déplacement du potentiel au cours du temps doit être continu.
Autrement dit, entre deux itérations de la simulation, le potentiel ne doit pas faire de " saut ",
sans quoi l'atome pourrait intempestivement quitter le piège.
Pour réaliser cette condition, on choisit le pas de simulation tel que,
pendant 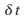 ,
le potentiel se déplace de 1/20e de sa largeur w.
D'après les equations (12) et (13),
on voit que, pendant un pas de simulation,
le potentiel se déplace d'un angle ,
le potentiel se déplace de 1/20e de sa largeur w.
D'après les equations (12) et (13),
on voit que, pendant un pas de simulation,
le potentiel se déplace d'un angle 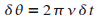 ,
et donc d'un distance ,
et donc d'un distance 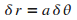 .
On impose la valeur de cette distance .
On impose la valeur de cette distance 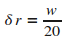 .
On en déduit la valeur du pas de simulation : .
On en déduit la valeur du pas de simulation :
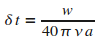
|
(15)
|
Nous avons maintenant un pas de simulation convenable,
nous pouvons donc résoudre numériquement les équations du mouvement, comme nous l'avons fait précédemment.
Nous obtenons alors la trajectoire de l'atome :
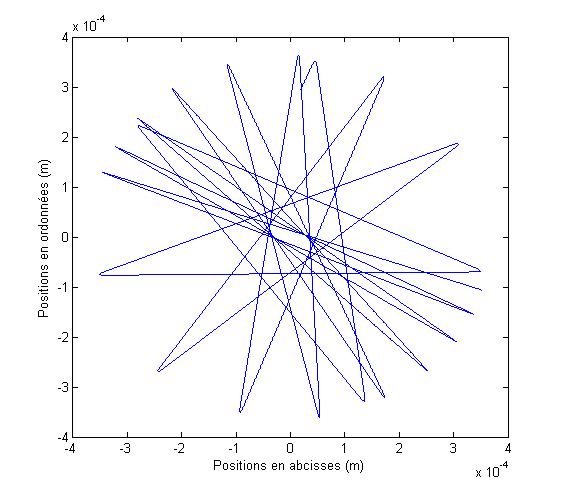
FIG. 7 - Trajectoire dans le potentiel dipolaire dépendant du temps
Visuellement, il semble que l'on observe bien un atome piégé dans un potentiel tournant.
Maintenant, nous décidons de faire une simulation avec les paramètres physiques de la manipulation.
Il convient alors de définir les constantes dans le code.
Dans le but d'obtenir une résolution la plus précise possible, nous n'utilisons dorénavant plus la "méthode d'Euler",
mais nous utilisons l'algorithme de Runge-Kutta d'ordre 4. Nous connaissons cet algorithme en langage C,
nous l'adaptons nous-même à MatLab.
Nous ne le détaillerons pas ici,
car nous nous apercevrons finalement qu'il induit une déviation numérique trop élevée pour observer un comportement
physiquement crédible (voir plus loin).
Comme pour la méthode d'Euler, nous devons définir un pas de simulation.
Nous utilisons donc le calcul expliqué précédemment.
Dans les conditions physiques de la manipulation,
nous obtenons 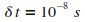 . .
Nous effectuons donc la simulation pour un atome, puis nous traçons sa trajectoire.
Nous obtenons un résultat similaire à la trajectoire précédente,
ce qui peut nous laisser croire que notre algorithme de Runge-Kutta fonctionne correctement.
Dans le cadre de notre étude, nous devons regarder l'énergie cinétique des particules.
Nous n'avons, à partir de maintenant, plus besoin de tracer de trajectoires.
La méthode Runge-Kutta, tout comme la méthode d'Euler, se fait en deux temps (intégration des accélérations pour obtenir les vitesses, puis intégration des vitesses pour obtenir les coordonnées).
La résolution numérique nous donne alors les vitesses et les positions à chaque instant.
Il est donc possible d'écrire l'énergie cinétique des atomes à chaque instant.
Ainsi, nous pouvons observer son évolution temporelle, puis quantifier le chauffage induit par les fluctuations force dipolaire.
Sachant que les énergies cinétiques mises en jeu sont de l'ordre de 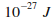 ,
pour ne pas dépasser la précision de l'ordinateur, nous comptons l'énergie cinétique en Kelvins.
Pour cela nous divisons l'énergie par la constante de Boltzmann k. ,
pour ne pas dépasser la précision de l'ordinateur, nous comptons l'énergie cinétique en Kelvins.
Pour cela nous divisons l'énergie par la constante de Boltzmann k.
A l'aide des coordonnées ( x(t), y(t) ), nous sommes capables de détecter un atome qui quitterait le piège,
et de vérifier, avec l'énergie cinétique,
que cette fuite provient effectivement d'une trop grande énergie de l'atome (qu'elle a donc chauffé) et non d'une erreur numérique.
Pour cela on compare l'énergie de l'atome à l'instant de sa sortie avec la hauteur du potentiel moyen (de l'ordre de 1000 µK).
Forts de cet outil numérique, nous effectuons la simulation sur 1000 atomes. Au bout de 7 jours, seulement 49 atomes ont été simulés.
En faisant une moyenne sur ces atomes, nous traçons l'énergie cinétique par atome.
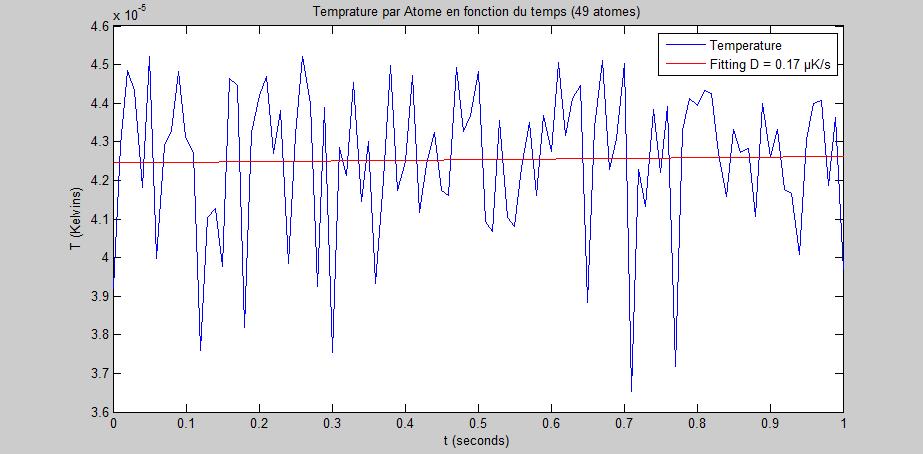
FIG. 8 - Energie cinétique par atome au cours du temps
Nous observons que le chauffage peut être considéré comme absent. Or, la théorie prédit que le chauffage doit être présent.
Nous réalisons d'autres simulations, et observons les résultats, dont voici un échantillon.
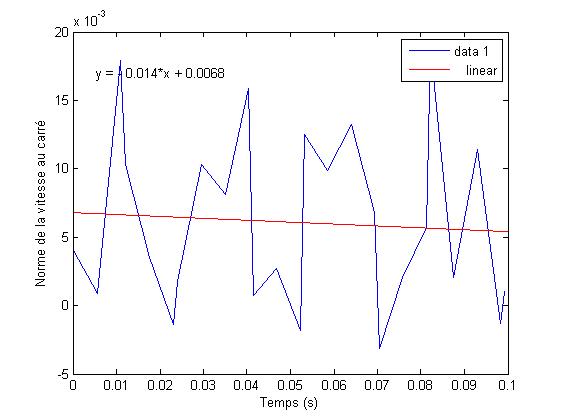
FIG. 9 - Energie cinétique par atome au cours du temps
Ici on observe même un refroidissement, ce qui est physiquement impossible.
Nous avons pris beaucoup de temps (environ les 4/5e du temps restant pour le projet tutoré) à essayer de modifier le code pour obtenir des résultats plus cohérents,
nous avons par exemple conçu un pas de simulation adaptatif
(dans la zone centrale du piège, il n'y pas d'interactions, on peut alors augmenter le pas de temps,
tandis qu'au voisinage du cercle décrit par le faisceau laser, les interactions entre atome et faisceau laser sont nombreuses,
le pas doit donc être le plus court possible).
Finalement, nous en avons conclu que notre algorithme de Runge-Kutta d'ordre 4 n'est pas assez précis,
la déviation numérique qu'il induit est trop élevée pour un tel problème physique.
Nous décidons alors d'apprendre à utiliser les fonctions de résolution numérique déjà implémentées dans MatLab
(par exemple ode45 ou ode15s).
Notre système d'équations différentielles est d'ordre 2.
Pour utiliser les fonctions de résolution de MatLab, il faut décomposer ce système d'équations en un système d'équations d'ordre 1 :
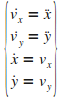
|
(16)
|
Nous traduisons ce système en langage MatLab, afin que les fonctions de résolution puissent le résoudre :
Il faut définir un vecteur X_dot = [ acc_x, acc_y, vx, vy ]
contentant les dérivées temporelles de chaque composante du système d'équations .
Et un vecteur X = [ vx, vy, x, y ] contenant les fonctions à résoudre.
Il suffit alors d'entrer cette commande dans MatLab
[t X] = ode15s( @acc, [0 tfin], [ vxini, vyini, xini, yini ], odeset( 'RelTol', 2.22045e-014, 'MaxStep', 1e-6, 'InitialStep', 1e-8 ) );
L'argument @acc appelle la fonction qui définit X_dot.
Le vecteur [ vxini, vyini, x,ini, yini ] contenant les conditions initiales.
La commande odeset( 'RelTol', 2.22045e-014, 'MaxStep', 1e-6, 'InitialStep', 1e-8 ) est nécessaire.
Elle permet:
- De réduire au minimum la tolérance relative de l'erreur à chaque pas de simulation.
-
De fixer un pas de simulation maximal permettant à l'atome de ne pas faire de trop grand "saut",
même quand le pas est maximal, sans quoi il risquerait de quitter le piège
- De fixer un pas de simulation initial convenable, sans quoi la résolution numérique est totalement fausse.
Nous obtenons alors un vecteur t contenant le temps à chaque pas de simulation,
et une matrice X composée de 4 colonnes contenant, respectivement,
les vitesses en x et y,
puis les coordonnées x et y, à chaque pas de simulation.
Nous réalisons alors une simulation sur 390 atomes (au bout de 7 jours),
et enregistrons le temps, les vitesses et les coordonnées de chaque atome dans un fichier
(en écrivant un fichier par atome).
Tout comme précédemment, nous observons l'énergie cinétique des atomes au cours du temps.
Cette fois-ci, nous observons effectivement un chauffage induit par la force dipolaire.
Nous pouvons alors le quantifier et en tirer les conclusions dans la partie exploitation.
|

