Simulation et interprétation des résultats

1. Méthode de simulation

Voici des illustrations de ce que l'on voit pendant la simulation :

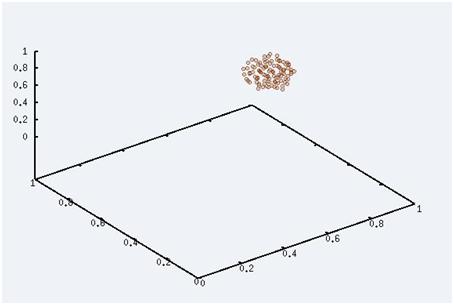
Cette photo du système a été prise à l'état initial, lorsque le système est à très faible température. On voit que toutes les particules sont regroupées entre elles formant un gros cluster. Nous sommes à l'état solide.

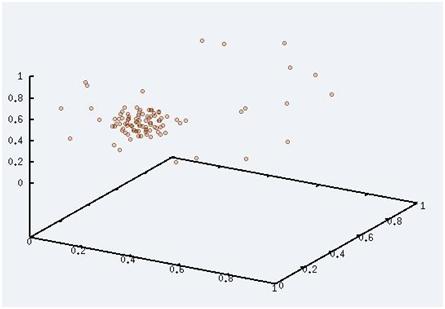
Maintenant, nous avons commencé à augmenté un petit peu la température. On voit que quelques particules commencent à se détacher du cluster. Nous sommes au début de la transition de phase.

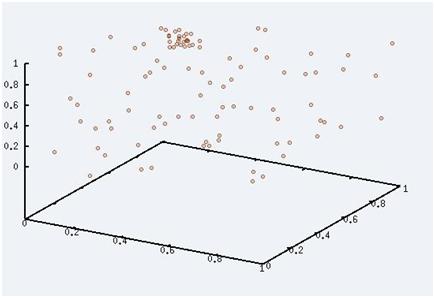
Nous sommes maintenant à température moyenne, nous voyons un mélange de particules libres, de paires et de petits clusters. Nous voyons une image prise pendant la transition de phase.

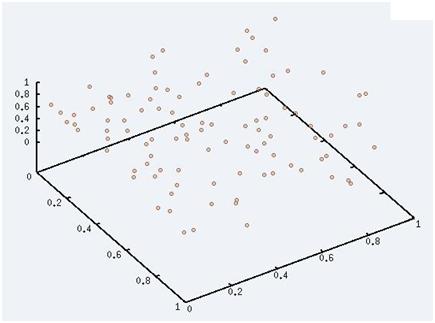
Cette photo a été prise à haute température. Nous pouvons voir que toutes les particules sont libres, il n'y a plus de paires, ni d'interaction entre elles (gaz parfait). Nous sommes à l'état gazeux.

1.1. Calcul de l'énergie totale et de la température

Pour obtenir des valeurs de la température en fonction de l'énergie, on fait varier l'énergie cinétique du système en multipliant les vitesses initiales des particules par un facteur. L'énergie du système se conserve (par définition) donc pour une énergie, si on attend que le système soit à l'équilibre, on obtient une température. Ainsi, si on augmente les vitesses initiales des particules du système, on augmente l'énergie cinétique, donc l'énergie totale et la température augmente.

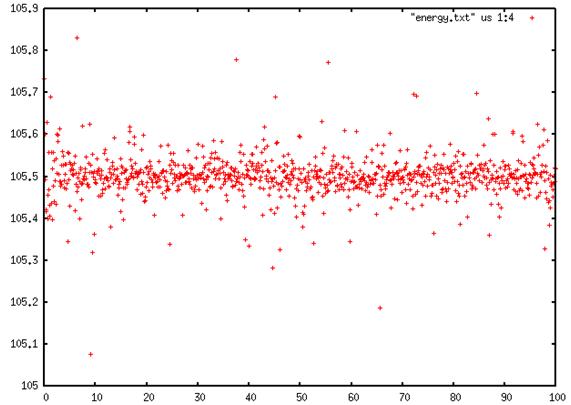
On voit sur ce graphique de l'énergie totale du système en fonction du temps est constante car l'énergie se concerve.

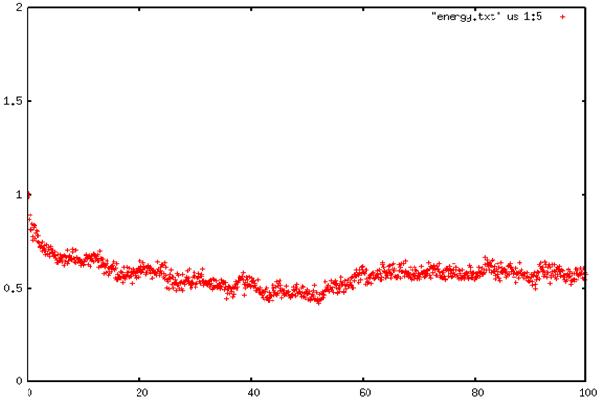
On voit qu'au bout d'un certain temps, la température en fonction du temps devient constante. Le système est alors à l'équilibre.

1.2. Calcul de la pression

Pour calculer la pression, on fait la somme de deux fois la quantité de mouvement v apportée par les particules lors de chaque choc contre les parois.

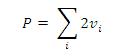
Pour cela, on ajoute au programme une nouvelle condition aux bords :

En traçant alors la courbe de la quantité de mouvement en fonction du temps et en déterminant to, l'instant ou le système s'équilibre

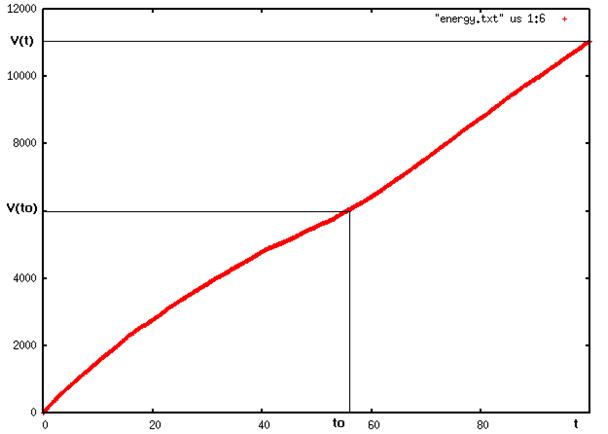
on peut calculer la pression du système.

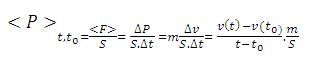
Avec S la surface et m la masse.

2. Interprétation des résultats

2.1. Température en fonction de l'énergie

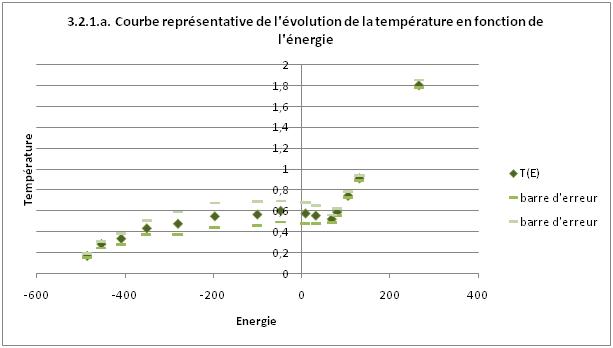
Sur ce graphique, on peut voir une transition de phase. On part d'un système solide à basse température. On commence à augmenter la température, les particules se mettent à vibrer à l'intérieur du solide. On voit ensuite que l'énergie continue d'augmenter mais que la température reste à peu près constante, on rentre dans la transition de phase.

On ne voit pas les deux transitions solide-liquide et liquide-gaz, on passe directement du solide au gaz avec une transition groupée où il y a une coexistence solide, liquide et gaz (on pourrait apparenter cette transition à une sublimation).

A la fin de la transition, on observe un phénomène physiquement impossible, l'énergie augmente et la température diminue. En effet, on a une pente négative, ce qui n'est pas possible car la chaleur spécifique à volume constant Cv est strictement positive.

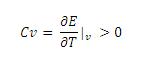
On peut le démontrer :

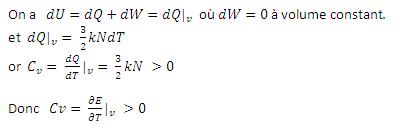
Cette erreur est surement due au fait que l'on augmente très vite la température, il aurait peu être fallu le faire plus progressivement.
On voit que la dernière partie de la courbe, après la transition de phase est linéaire.
On sait que E= 3/2 NkT pour un gaz parfait.
Donc la pente théorique de la droite est P_th=0,0067 avec k=1, et N=100 particules.
Sur le graphique, on trouve une pente expérimentale P_exp=0,0065.
On peut donc dire qu'après la transition de phase, nous sommes en présence d'un gaz parfait.

2.2. Température en fonction de la pression

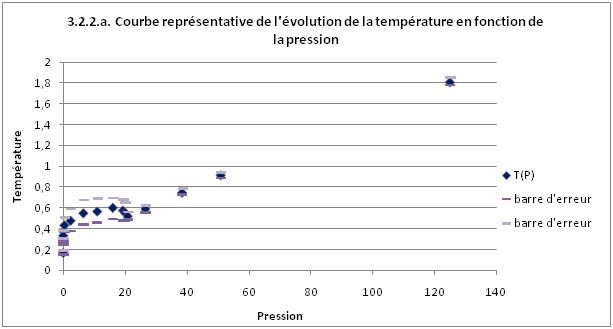
On voit que lorsque le système est à l'état solide, à basse température, la pression est nulle, ce qui est cohérant puisque il n'y a pas de chocs des particules contre les parois.

Ensuite, on voit qu'au fur et à mesure que l'on augmente la température, la pression augmente jusqu'à la transition de phase où la pression augmente à température reste plus ou moins constante.

On retrouve la même anomalie que sur le graphique précédent (T=f(E)) à la fin de la transition de phase, la température diminue alors que la pression et l'énergie continuent d'augmenter.

Et enfin, à la fin de la transition de phase, on a une partie de la courbe qui est linéaire.
On sait que PV=NkT, avec k=1 et N=100 particules.
Et on trouve une pente expérimentale P_exp=0,0123 qui correspond bien à la pente théorique P_th=0,01 d'un gaz parfait.

2.3. Pression en fonction de l'énergie

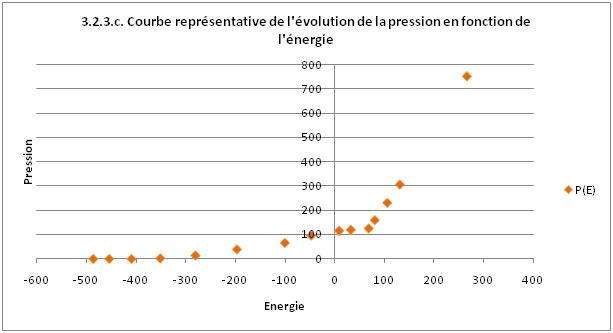
Sur cette courbe, nous n'avons pas mis les barres d'erreurs car elles sont négligeables devant l'échelle du graphique.

Nous obtenons ici un graphique cohérent avec les deux précédant, en effet, la pression augmente lorsque l'énergie augmente, qui sont elles deux liées à la température qui augmente.