Résultats
Dans cette partie, nous présenterons nos résultats sur l’étude de la surface fractale du dépôt de TiO2.
1) Quelques notions sur les fractales :
Un objet fractale est un objet mathématique dont la structure est la même à toutes les échelles.
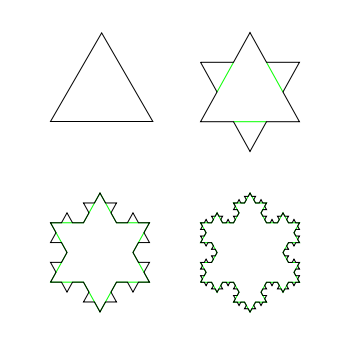
Une fractale présente quelques caractéristiques :
- elle est auto-similaire à l’infini, c’est-à-dire que sa forme générale est semblable à une de ses parties quelques soit l’échelle,
- elle est trop complexe pour être décrite avec la géométrie classique,
- elle possède une dimension fractale qui n’est pas entière et qui la caractérise, en effet la longueur entre deux points d’une fractale est infinie et n’a donc plus de sens ici.
En mathématique, ces objets sont considérés comme des « monstres mathématiques » et c’est Mandelbrot qui a montré, en 1982 («The fractal geometry of Nature»), la réalité, et l’applicabilité de la géométrie fractale.
Il existe dans la nature des objets fractals : le chou romanesco, une fougère, les bronches …

Cependant, les objets fractals naturels ne sont pas parfaitement auto-similaires à l’infini.
2) Résultats de l’étude du dépôt de TiOR₂ :
- Mesure du diamètre moyen des particules de TiO2 :
Mesuré avec un spectromètre à corrélation de photon dans le sol-gel : d = 6.5 nm.
- Etude du dépôt au microscope :
On observe au microscope :
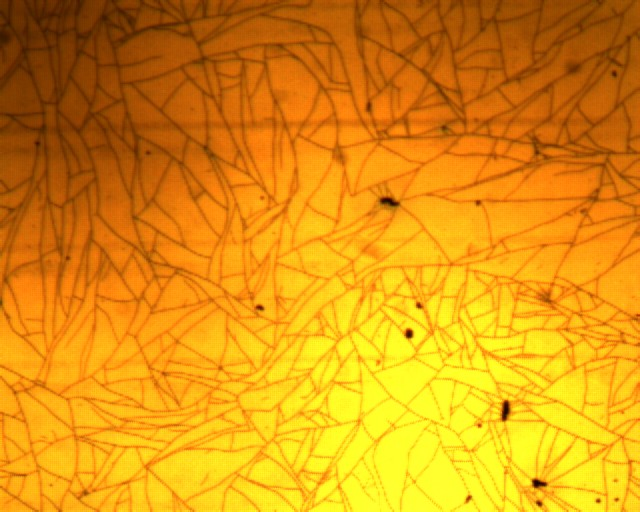
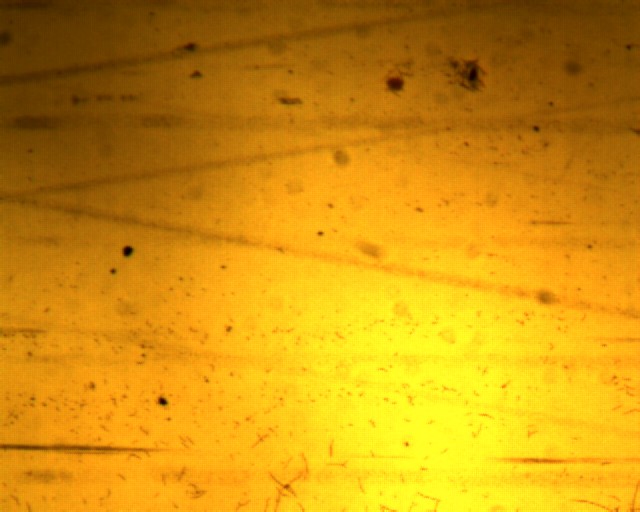
Des zones où le dépôt est très fin presque transparent ou notre dépôt est correctement fait,
D’autres zones où le dépôt est fracturé et brunâtre ou le dépôt est mal fait.
- Calcul de la dimension fractale, df, de la surface du dépôt de TiO₂ :
Le df est assimilable à un « taux de remplissage d’espace », en effet si on divise l’espace en cellules d’aire a, le nombre N(a) de cellules nécessaires pour recouvrir la surface suit la loi :
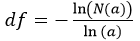

Expérimentalement, ceci consiste à lier des particules sur le TiO2 et mesurer le nombre de ces particules adsorbées. Nous avons utilisé la phtalocyanine de cuivre (PB15).
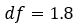
Cette dimension n’est donc pas entière notre dépôt est donc bien fractal.
- Calcul de la surface spécifique de la couche TiO₂ :
Nous avons démontré précédemment que le dépôt de TiO₂ possède une surface fractale, donc la surface de la couche de TiO₂ devrait être nettement plus grande que la surface de la plaque. On appelle cette surface, divisée par la masse de TiO₂ sur la plaque, la surface spécifique.
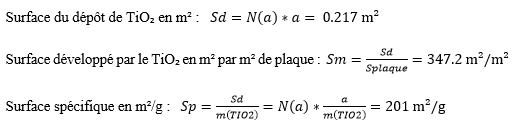
La surface développée par le TiO₂ est donc très grande par rapport à la surface de la plaque.
Comparaison avec la valeur théorique donnée par :
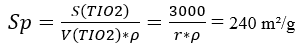
C’est la surface spécifique que devrait normalement développer nos particules de TiO2 si le dépôt est correctement fait. avec
S(TIO2)= surface d’une particule de TiO₂ ;
V(TIO2)=volume d’une particule de TiO₂;
ρ = 3.84 g/cm³ = densité du TiO₂;
r = 3.25nm = rayon d’une particule de TiO₂,
Ces deux valeurs de Sp diffèrent un peu. Explication :
-ce calcul ne donne qu’une estimation de la surface spécifique car on néglige les distances inter-particulaires ;
- la totalité de la plaque de verre n’était pas correctement recouverte de TiO₂ ;
- Calcul de l’épaisseur moyenne du dépôt de TiO₂ :
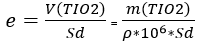
V(TIO2) = volume du dépôt de TIO2 sur la plaque.
Dans le cas d’une couche fractale, cette épaisseur est estimée à 0.1 µm en prenant comme densité effective de la couche :
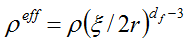
où "Xi" est la longueur de persistance évaluée à 100 nm dans le cas de TiO2. On a bien une couche très fine nanométrique de TiO2 sur la plaque.
Grace à cette étude de notre dépôt de dioxyde de titane, nous avons bien mis en évidence l’aspect fractal de ce dépôt et ainsi sa grande surface spécifique et son épaisseur nanométrique.
Pour plus de detail , voir le Compte rendu : Cellule photovoltaique de Graetzel
