Partie Experimentale

Mesure de la durée de vie τ :

a) Matériel Utilisée:

   - Driver ( ITC4001 )
   - Diode Laser ( PL980 P330J )
   - Isolateur optique ( 10-F-980-APC)
   - Fibre optique SMF28 et SMF980
   - Fibre EDF J-07
   - Ossciloscope (LECROY 9344C )
   - Câble BNC
   - WDM (S/N 01364110)
   - Photodétecteur (P-400-FC-2)
   - Graisse optique d'indice no=1,46

b) Protocole Expérimentale:

      Pour déterminer la durée de vie du niveau 2, nous avons besoin d'un oscilloscope afin de représente l'échelle de temps et d'un générateur de fonction (driver) qui permettra de fournir des signaux variables au cours du temps .
Nous imposons au générateur de fournir des fonctions carré pour pouvoir couper la pompe et ainsi observer la désexcitation de la population du niveau 2.
Nous utiliserons une photodétecteur afin de convertir la fluorescence émise par la fibre en tension électrique ce qui nous permettra de visualiser sur l'oscilloscope la variation de tension en fonction du temps.
D'aprés l'étude théorique (section spectroscopie des terres rares), nous savons que la population du niveaux 2 suit une loi de décroissance exponentielle.
Dès lors nous pouvons écrire la tension comme :

V=Vo.exp(-t/τ)
Avec Vo : la tension à t=0.
              τ :   la durée de vie.

c) Montage Expérimentale:

Figure1
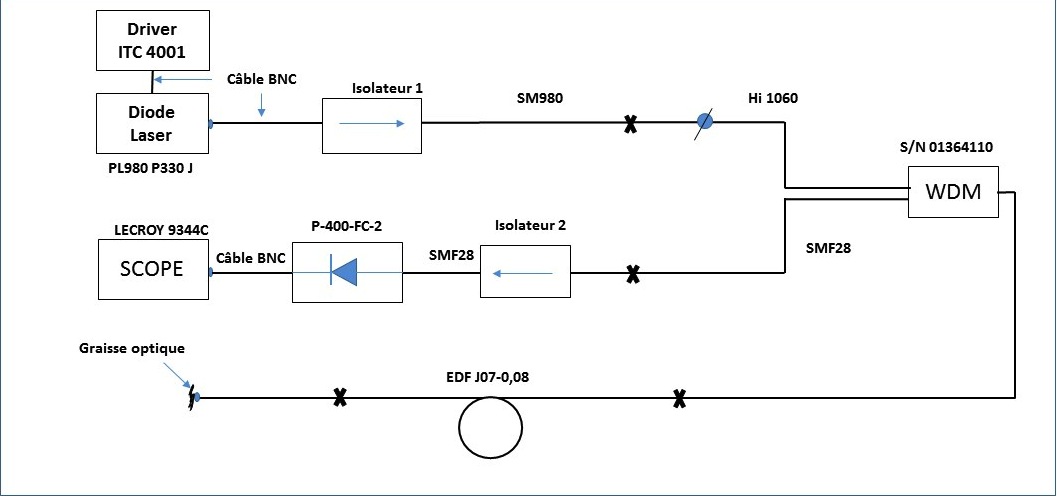
d) Résultat:

Nous avons fait la mesure pour τ , 2τ , 3τ et nous obtenons le graphe suivant:

Echelle semi-log Echelle linéaire

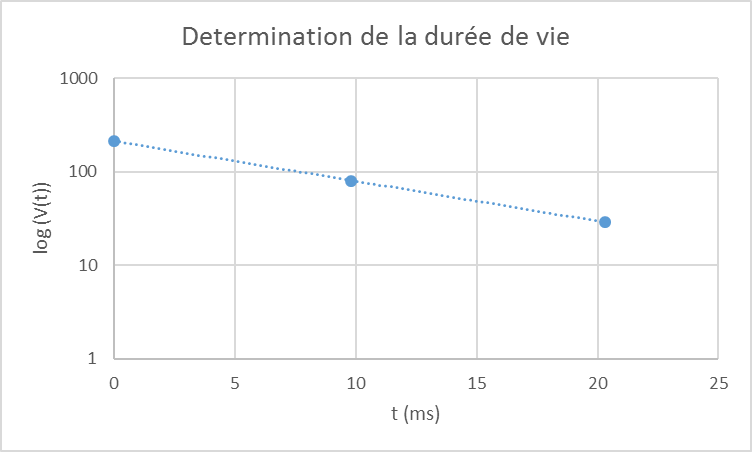
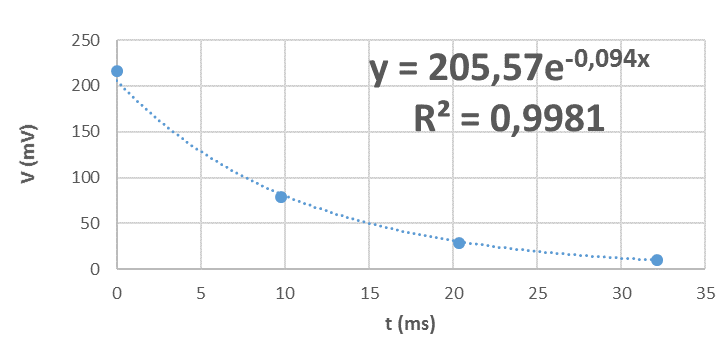
Figure2: représentation de la tension en fonction du temps
De ce graphe nous en déduissons une équation de la tension qui s'écrit:

V=205,57.exp(-0.094t)
avec 1/τ = 0,094 s^-1

d'où τ=10,63 ms

calcul d'incertitude

pour calculer l'incertitude sur la durée de vie, on a choisit la méthode graphique on détermine la pente maximale et la pente minimale de la courbe en échelle log :

1/ τ₁ = 0,102 ms^-1 <=> τ₁ = 10,53 ms

1/ τ₂ = 0.095 ms^-1 <=> τ₂ = 9,80 ms

Donc Δτ = ( τ1 + τ2 ) / 2

Δτ = 0,36 ms
Resultat final:
τ=10,63 ± 0,36 ms