THEORIE - Index
THEORIE
Ernst Chladni (né en 1756, mort en 1827) est un physicien allemand qui a étudié les phénomènes acoustiques de manière expérimentale, notamment les vibrations dans les plaques. Il est le premier à avoir eu l´idée de placer du sable sur les plaques qu´il faisait vibrer afin d´observer les figures de résonance portant aujourd´hui son nom.

Fig. 1 : Portrait de Ernst Chladni.
La méthode étant assez simple, il suffit de frotter les plaques en question à leur bord pour exciter les modes de vibrations, le sable evitant les ventres, ce sont les zones comportant le maximum de vibration, et se plaçant ainsi au niveau des lignes nodales, ce sont les zones comportant le minimum de vibrations.

Fig. 2 : L'excitation de la plaque permet de visualiser la figure de Chladni correspondant à la fréquence de résonance, ce n'est qu'une seule des figures observables sur celles correspondant à l'ensemble des modes pouvant être éxcités.
Chladni met ainsi en évidence le phénomène de résonance d'un objet vibrant lorsqu´il est excité selon certaines fréquences.
Wallace Clement Sabine (né en 1868, mort en 1919) est un physicien américain considéré comme le fondateur de l´acoustique des salles : il a lui aussi étudié les phénomènes acoustiques de manière expérimentale et établit certaines formules de façon empirique encore utilisées aujourd´hui en acoustique architecturale.

Fig. 3 : Portrait de Wallace Clement Sabine.
Il découvre le temps de réverbération, c'est à dire le temps au bout duquel un son n'est plus audible après interruption de la source sonore. Il met en évidence le phénomène de réverbération, et pose ses premiers principes :
Premier principe : le son provenant d'une source se diffuse dans la plupart des pieces de n'importe quel point source, de façon uniforme dans l'espace et dans toutes les directions au cours du temps.
Second principe : Chaque fois qu'un son est réfléchi sur une surface on note une perte d'énergie qui dépend de la fréquence et du matériau qui constitue la surface.
On peut donc déterminer quelle quantité d'énergie est perdue en fonction des caractéristiques de la surface.
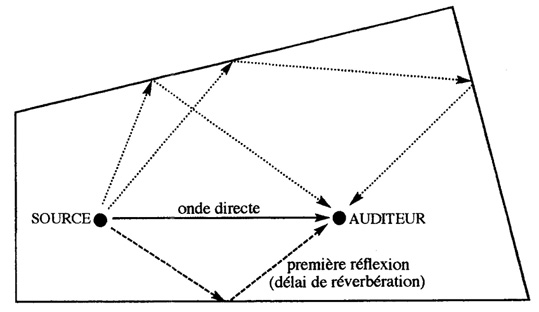
Fig. 4 : Réflexions multiples d'un signal sonore.
On a vu que Chladni avait réussi à exciter les modes de vibration d'une plaque et à visualiser les figures de résonance. Dans le cas de l'excitation via un archet la fréquence de résonance n'est pas imposée, on utilisera par la suite (dans nos experiences) un haut-parleur pour imposer la fréquence d'excitation. Car ces figures diffèrent en fonction de la fréquence d'excitation, des caractéristiques, des dimensions de la plaque utilisée et des zones d'application de l'excitation. En effet une figure ne pourra être visible que si le mode correspondant à la fréquence d'excitation n'est excité qu'en ses ventres et non sur ses lignes nodales. Par exemple, pour une plaque carrée appuyée sur ses bords, de côté a et d'épaisseur h, orientée suivant les axes x,y,z, selon la longueur, la largeur et l'épaisseur, les formations des lignes nodales varient en fonction da l'amplitude de déplacement :
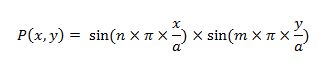
Et on détermine les modes de cette plaque, en considérant son élasticité isotrope, par la formule :
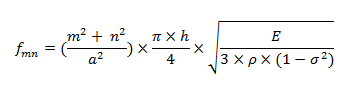
σ : le coefficient de Poisson,
ρ : la masse volumique,
E : module d'Young,
a : la longueur et largeur de la plaque,
h : l'épaisseur de la plaque.
Le temps de réverbération c'est le temps que met un signal sonore pour être inaudible après que le signal source a été coupé. Il est également appelé RT60, car après une chute de 60dB de l'intensité du signal, un son d'intensité moyenne devient inaudible. C'est en partie une convention qui à été adoptée d'après la sensibilité de l'oreille humaine.
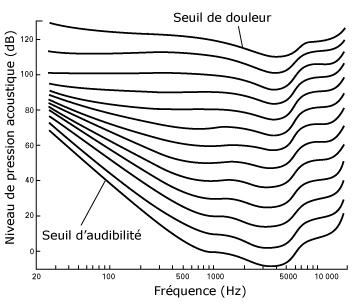
Fig. 5 : Courbe de la perception de l'intensité du signal en fonction de la Fréquence pour une oreille humaine.
Ainsi de façon mathématique on définit ce RT60 dans une salle comme :
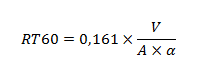
A : la somme des airs de chaque mur,
α : le pourcentage d'énergie perdue après chaque réflexion.
On définit le RT60 dans une plaque comme :
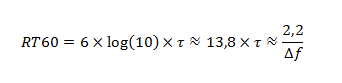
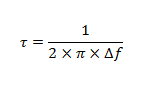
Δf : la largeur à mi-hauteur du pic correspondant à la fréquence de résonance sur le spectre de puissance du signal, on reviendra sur cette définition.
On remarque que ces formules utilisent une échelle logarithmique, en effet c'est parce que le signal enregistré, après extinction de la source, suit idéalement une décroissance exponentielle.
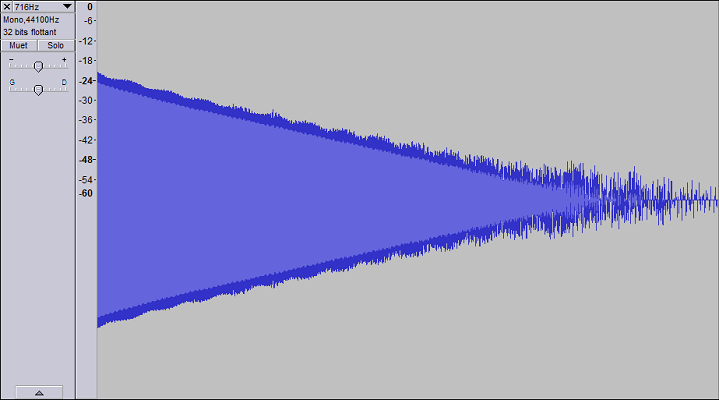
Fig. 6 : Enregistrement d'un signal pendant le temps de réverbération, on remarque une certaine linéarité de la décroissance du signal sous échelle logarithmique. Une décroissance tout à fait linéaire signifierait l'enregistrement d'une seule résonance, ou de plusieurs résonances de même largeur à mi-hauteur de leur pic de résonance.
Le spectre de de puissance du signal sonore enregistré permet d'étudier les pics de résonance de chaque fréquence de résonance du signal. Ce spectre correspond au module carré de la transformée de Fourier du signal :
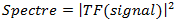
C'est sur ce spectre que nous allons pouvoir observer les fréquences de résonances les plus importantes. En relevant la largeur à mi-hauteur (le Δf) du pic de résonance le plus bas en fréquence et qui atteint un maximum d'intensité (correspondant à la fréquence fondamentale), On peut ainsi retrouver le temps de réverbération du signal grâce à la formule donnée précédemment.
Bien entendu on effectue cette analyse sur la partie décroissante du signal, aprè extinction de la source : lorsque le système vibrant atteint son régime amorti libre.
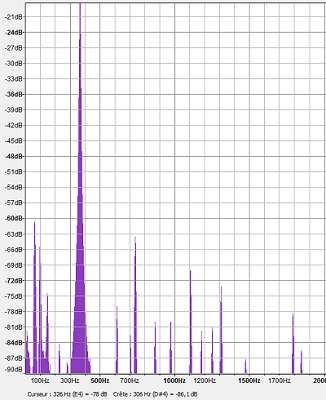
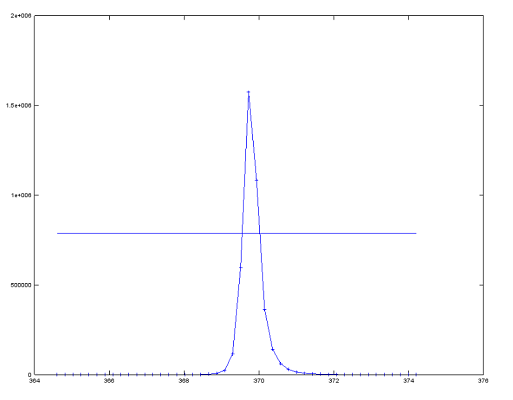
Fig. 7 : Spectre de puissance du signal sonore, on étudie le pic le plus haut qui correspond à la fréquence fondamentale, ici 369Hz, pour ce mode de résonnance.
Fig. 8: On relève la largeur à mi-hauteur du pic (ici analyse sous Octave) pour retrouver le temps de réverbération.