La théorie

Les origines du tsunami

L´origine du tsunami se situe généralement loin du regard de l'homme , comme le plancher océanique. Ainsi il n´à pas toujours été évident de comprendre d'où cette vague déferlante provenait...

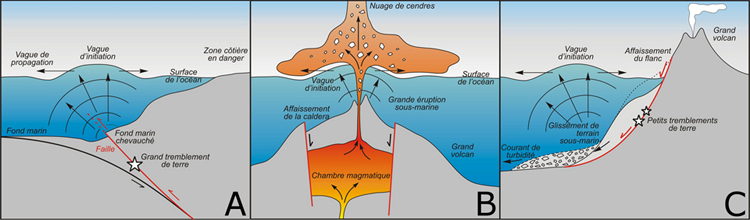
Aujourd´ hui, on sait qu´ un tsunami peut avoir diverses origines, qui correspondent à des événements devant déployer une énergie suffisamment importante pour déplacer une grande masse d'eau. En effet, la perturbation soulève cette masse brusquement, puis par les effets de la gravité, pour retrouver un système à l'équilibre, la propagation s'amorçe.
Ces évènements peuvent correspondre à:

  • Des séismes sous-marins d´une magnitude ou égale à 6.3, et dont l´épicentre se situe à moins de 50 km de la surface; [A]
  • Une explosion volcanique sous-marine; [B]
  • Des glissements de terrains; [C]
  • La chute d´un objet de grande ampleur tel une météorite, l´effondrement d´une montagne,…




    • La propagation


    La propagation du tsunami consiste donc en un déplacement d'une colonne d'eau entière dans deux milieux distincts :

  • en eau profonde, soit le large, la "haute mer" ;
  • et à l'approche des côtes maritimes ;

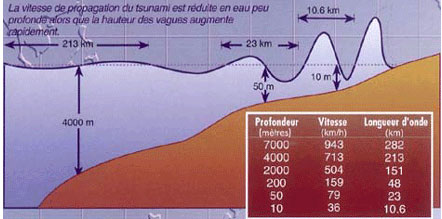
    • Cependant, la plupart des tsunamis ont une longueur d’onde supérieure ou égale à la centaine de kilomètres. Leur longueur d’onde est donc très supérieure à la profondeur des océans qui ne dépasse pas la dizaine de kilomètres. C’est pourquoi, dans le cas des tsunamis on parle de « vague en milieu peu profond » (dit "shallow water").


    Remarque : En raison de la friction à l'approche des côtes, la célérité diminue. La période étant conservée, on en déduit que la longueur d'onde diminue également. Cependant, elle reste tout de même, que ce soit au large ou à l'approche des côtes, bien supèrieure à la profondeur.


    En étudiant les lois qui régissent la mécanique des fluides, cette caractéristique dite "peu profonde " permet de faire plusieurs approximations qui permettent d'écrire deux équations, caractérisant la physique à laquelle obéit le tsunami :

  • Loi de célérité du tsunami :
    v= √(g*h0) ;
  • Equation de propagation du tsunami :
    ∂^2/∂t^2 [h'] - (h0-ax) g * ∂^2/∂x^2 [h'] + ag * ∂/∂x [h'] = 0 ;

    • (avec : h' = h - h0 ;)

    Où :
    v : la célérité ;
    h0 : hauteur d'eau initiale ;
    h (x,t) : hauteur d'eau ;
    a : pente du fond maritime ;
    g : accélération de la gravité ;

    Ces équations permettent d'en déduire notamment deux applications :

  • La première permet permet d'en déduire le temps mis par un tsunami pour arriver jusqu'à la côte. Par exemple, dans le cas d'une profondeur d'eau de 4000m, avec un tsunami caractérisé par une longueur d'onde de 200 km, on calcule la célérité équivalente à 200m/s. Ainsi, pour des côtes situées à 4000km de l'origine, le tsunami les atteint en 5 heures et 33 minutes. Ainsi, si le tsunami est repéré suffisamment tôt, cela laisse le temps d'appliquer les règles de sécurité, qui consiste à se placer en un point élevé ou à s'éloigner en haute mer pour les bateaux.



  • La deuxième équation, permet, quant à elle, d'en déduire, suite à l'approximation ax << h0 (la pente du fond maritime est très faible devant la hauteur d'eau initiale), une estimation de la variation de h'. Cette estimation correspond notamment au coeur de notre étude et est notamment illustrée par notre expérience.

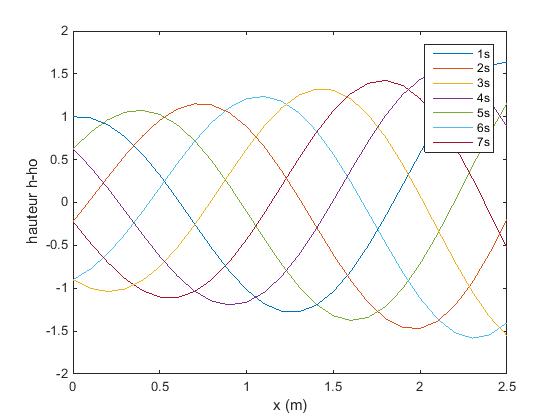
    • Ainsi, un résultat de l'équation est :

    h'(x,t) = exp(-ki * x ) cos(kr * x - w * t) ;

    Où :
  • ki (composante imaginaire du vecteur d'onde) = - a / 2h0 ;
  • kr (composante réel du vecteur d'onde) = ± 1/c0 √(ω^2-(g*a^2)/4h0) ;
  • w : la pulsation ;
  • c0 : célérité initiale de l'onde ;


    • Remarques :
  • Le terme en cosinus correspond au terme de propagation du tsunami.
  • Le terme exponentiel correspond au terme d'amplification de l'onde et la théorie permet de mettre en évidence que celle-ci croit avec la pente. C'est notamment un des points que l'on cherche à démontrer avec nos expériences .