Dans cette partie, nous étudierons les concepts d'interférences multimodales et de ré-imagerie (reimaging).
Pour cela, nous allons dans un premier temps effectuer des expériences nous permettant d'observer les interférences des modes de propagation de la lumière à l'intérieur d'une fibre optique.
Sachant que les modes se propagent à des vitesses différentes et donc à des phases différentes en un point donné de la fibre,
nous allons, dans une deuxième partie, déterminer la longueur pour laquelle la différence de phase entre deux modes est égale à 2π, c'est à dire la longueur de fibre multimode à la quelle
on aura ré-imagerie du mode excitateur.
Nous allons dans cette partie, après avoir soudé une fibre monomode à une fibre multimode, essayer de déterminer la longueur de la fibre multimode nécessaire pour avoir réimagerie du mode excitateur de la fibre multimode, c'est à dire on cherche la longueur pour laquelle on aura un maximum d'intensité au centre de la figure d'interférence. Nous avons choisit d'étudier seulement les modes LP0m ( Voir partie théorique: ici ), dont la forme représente des anneaux concentriques. D'après la formule (dans le rapport) suivante, on peut calculer facilement la longueur de ré-imagerie: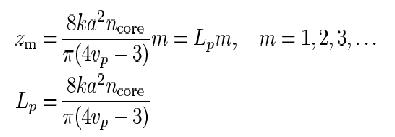
ncore est l’indice du cœur de la fibre ncore = 1.45
a est la taille du rayon du cœur de la fibre : a = 62.5 µm
k = 2π/λ avec λ la longueur d’onde du laser : λ = 632.8 nm
ʋp représente l'ordre du mode LP0ʋ et sa valeur est choisie grâce à la courbe suivante prélevée de l'article[réf1]:
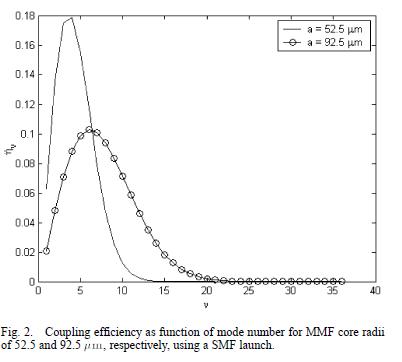
Pour a = 52.5 µm on a V = k.a.ON = 67.7 à 1.55 µm
Pour a = 92.5 µm on a V = 119
Dans l'article, la fibre a une différence d'indice de réfraction: ∆n = 1.479-1.444 = 0.035 (à 1.55 µm) ON = 0.318.
Or dans notre cas, V = 657, mais comme l'article montre que seulement quelques modes LP0m sont excités, on peut dire donc qu'on est dans la même situation et utiliser la courbe ci-dessus.
Le rayon du cœur de notre fibre est de 62.5 μm, la courbe de ƞʋ en fonction de ʋ correspondante est donc comprise entre ces deux courbes (a=52.5 μm et a=92.5 μm). ʋp correspond au maximum de la courbe. Nous choisissons ʋp = 5.
En effectuant le calcul, on trouve donc: Lp = 8.42*10-3m En prenant différentes valeurs de m on trouve bien des multiples de 8.42 :
Pour m = 1, z = 8.42mm
Pour m=2, z = 17 mm
Pour m=3, z = 25.5 mm
pour m=4, z= 33 mm etc.
Nous allons à présent effectuer les observations des interférences des modes sortant d'une fibre monomode soudé à une fibre multimode de différents longueurs de z.
On s'attend donc à avoir la réimagerie du mode fondamental à ces valeur de z (maximum d'intensité au centre de l'image)
On soude maintenant notre fibre monomode initiale à une fibre multimode sans cœur de diamètre=125 μm et d'indice de la gaine n=1 (car c'est l'air) comme sur le schéma qui suit:
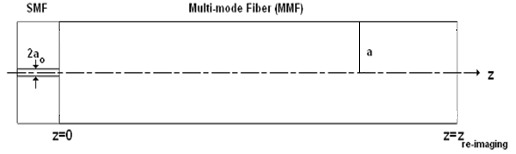
On fait varier, ensuite, la longueur z de la fibre multimode afin de pouvoir observer la superposition des modes à la sortie de notre système et de trouver ainsi la longueur de ré- imagerie du mode fondamental (voir la partie théorique).
Pour pouvoir tenir la fibre, lorsqu’on veut la cliver à une distance assez petite, par exemple enlever 1mm, on doit rallonger notre fibre multimode. Pour cela on soude un autre tronçon de fibre quelconque à chaque fois avant le clivage. A la fin on vérifie si le clivage a été bien fait avec la soudeuse.
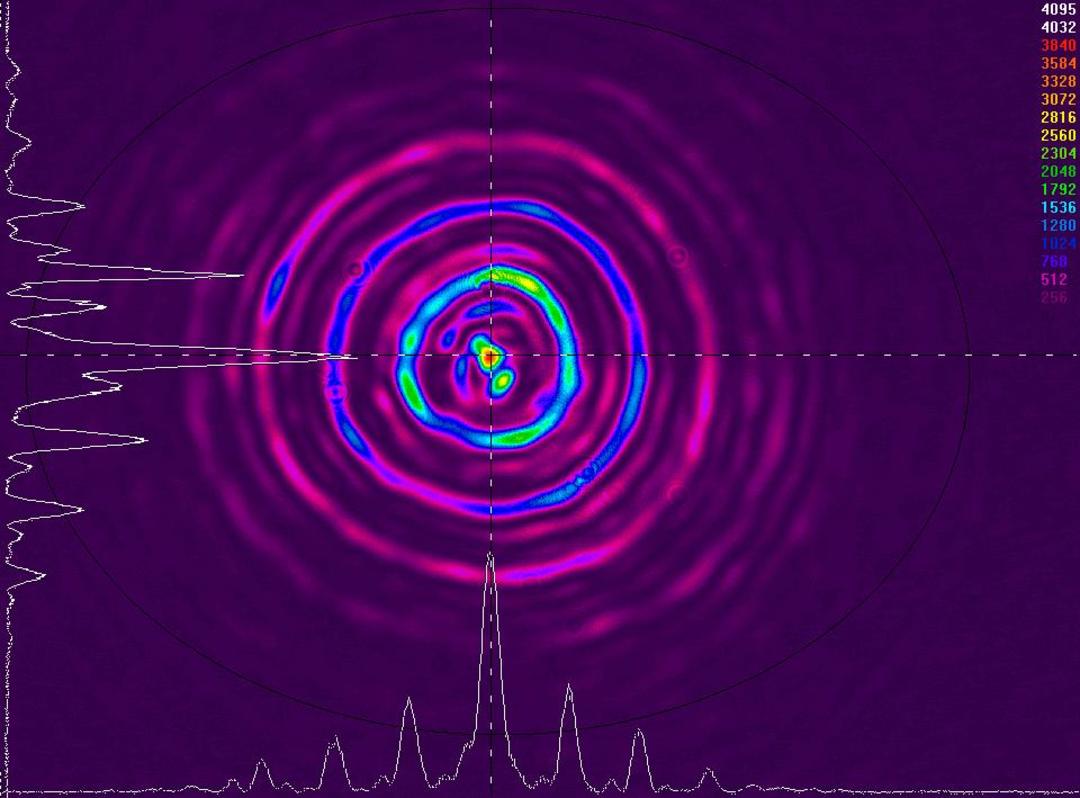
On commence par observer l'interférences des modes à la sortie de notre système (SMF-MMF) en prenant une longueur à peu près z= 9 mm. On obtient donc l'image suivante:
observation des interférences des modes en champ lointain à z = 9 mm
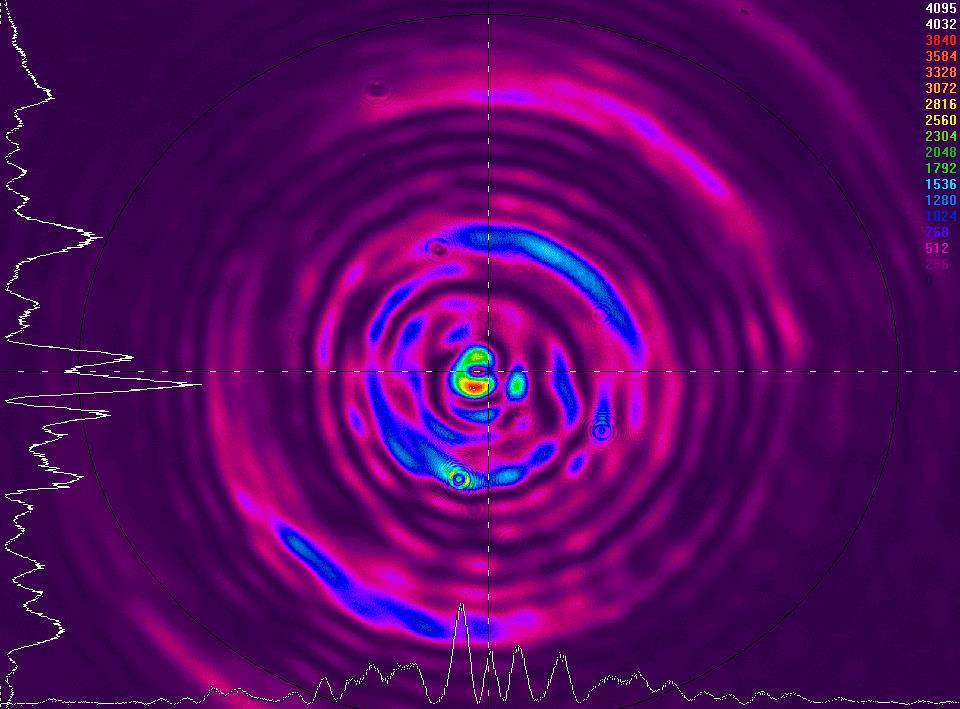
observation des interférences des modes en champ lointain à z = 18 mm
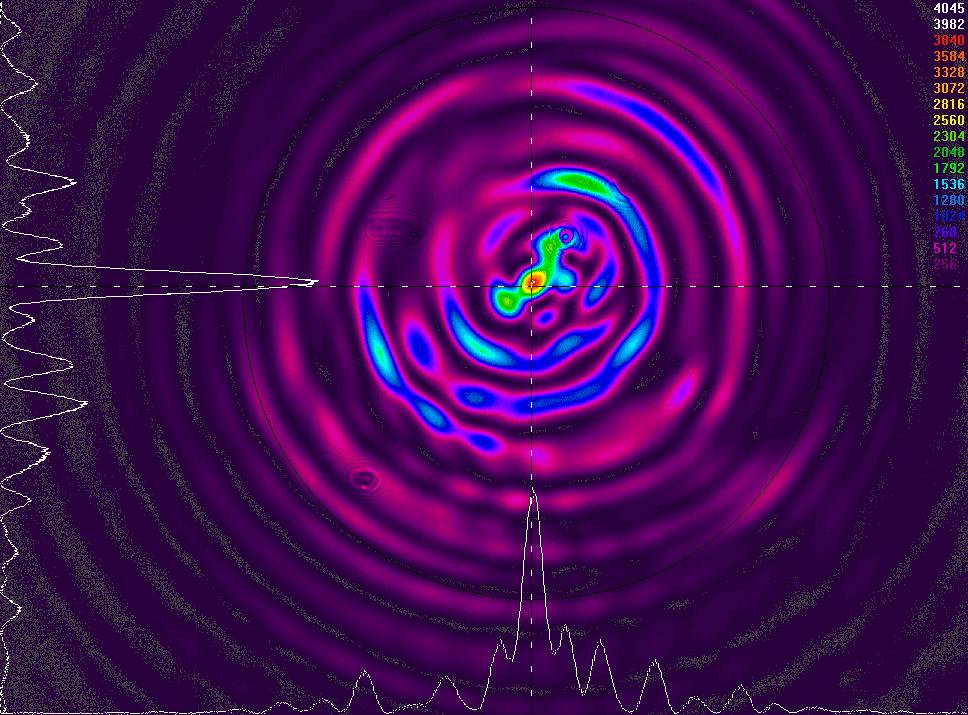
Puis on prend une longueur de la fibre multimode z = 27mm:
observation des interférences des modes en champ lointain à z = 27 mm
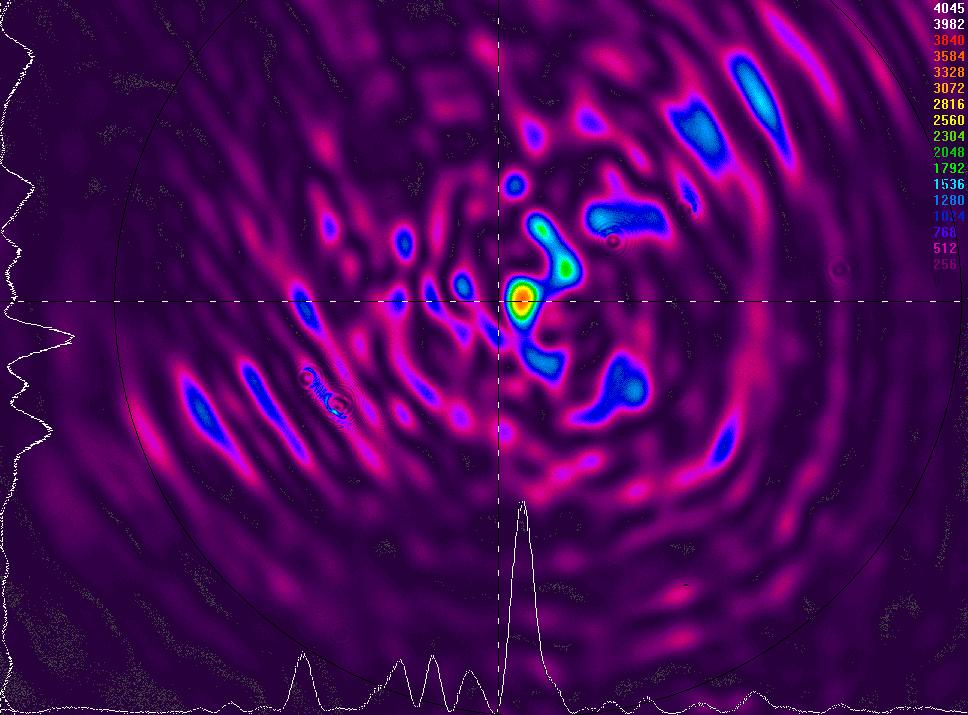
Après avoir varié plusieurs fois la longueure de la fibre multimode, on obtient une longueure très interressante à savoir z=33 mm:
observation des interférences des modes en champ lointain à z = 33 mm

On constate qu’il existe plusieurs valeurs de z ou l’intensité est maximale au centre : 9 mm, 18 mm, 27 mm, et 33 mm. Ceci représente la ré-imagerie du mode fondamental.
On constate également que ces longueurs sont pratiquement des multiples de 9, en effet cela correspond aux longueures de ré-imagerie théoriques calculées précedemment.
La meilleur observation que nous avons obtenu est celle de 33mm, en effet c'est celle qui se rapproche le plus de la théorie:
avec m=4 on z= 4*8.42 = 33.68 mm.
En faisant nos mesure, nous avons constaté sur quelques images (comme nous le voyons sur l'image qui suit) une forte intensité suivant un axe transverse et une intensité très faible ailleurs, ceci peut être dû à un mauvais clivage.
Observation des interférences des modes en champ lointain à z = 33 mm (Mauvais clivage)
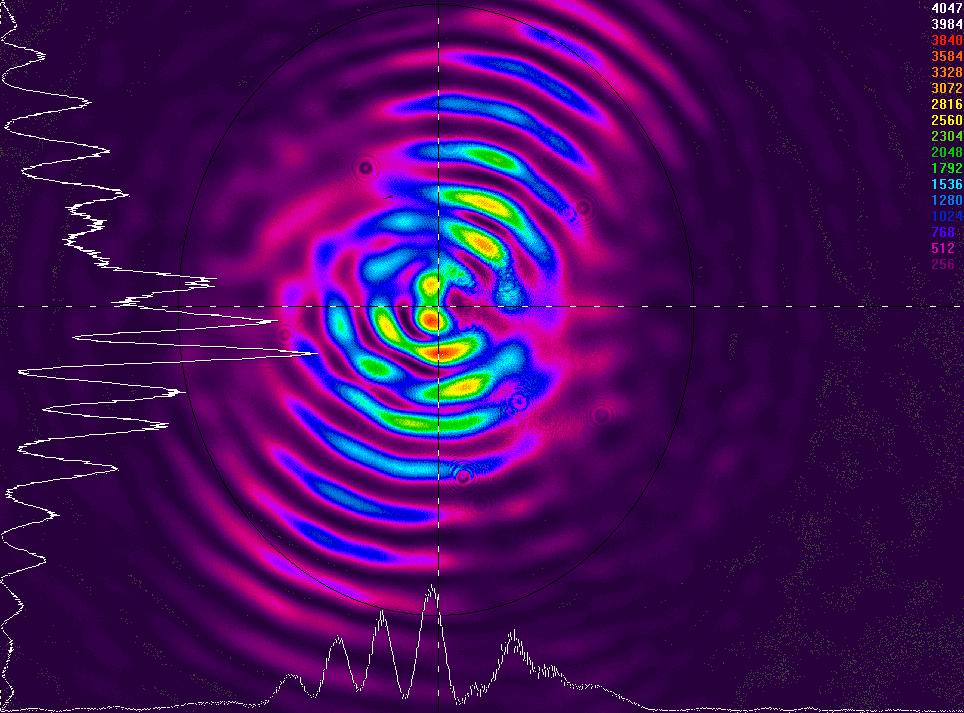
Observation des interférences des modes en champ lointain à z = 33 mm (Bon clivage)

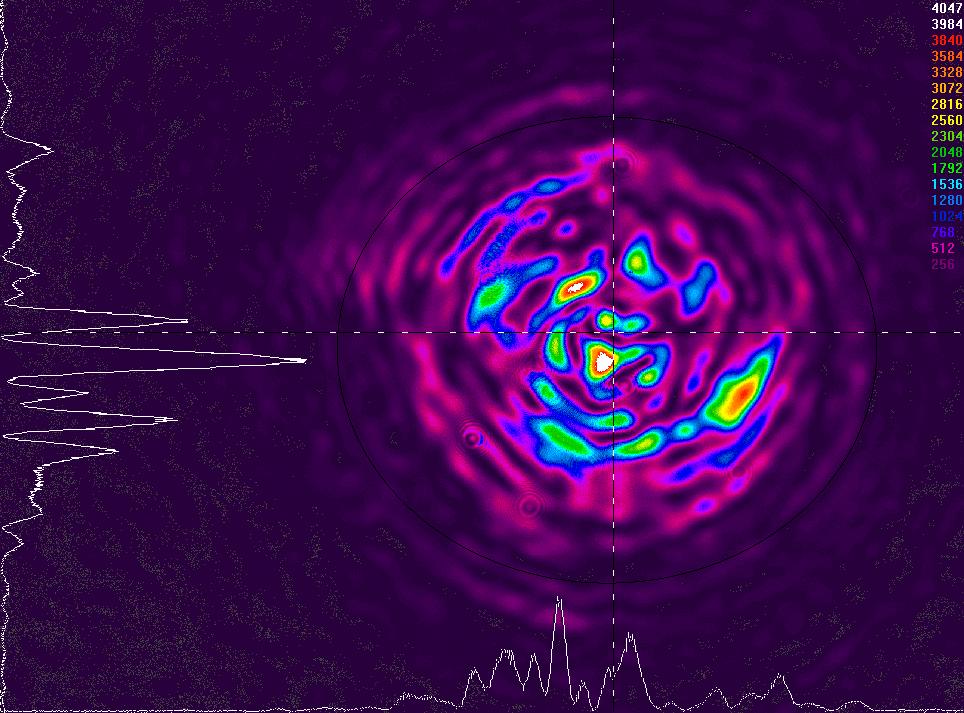
Durant nos expériences, on a obtenus des images sur lesquelle on a une concentration de l'intensité lumineuse suivant un axe transvers malgrès le bon clivage,on a alors effectué des images des interférences des modes avant et après soudure automatique, on obtient les images suivantes :
Observation des interférences des modes en champ lointain à z = 103 mm (Avant soudure automatique)
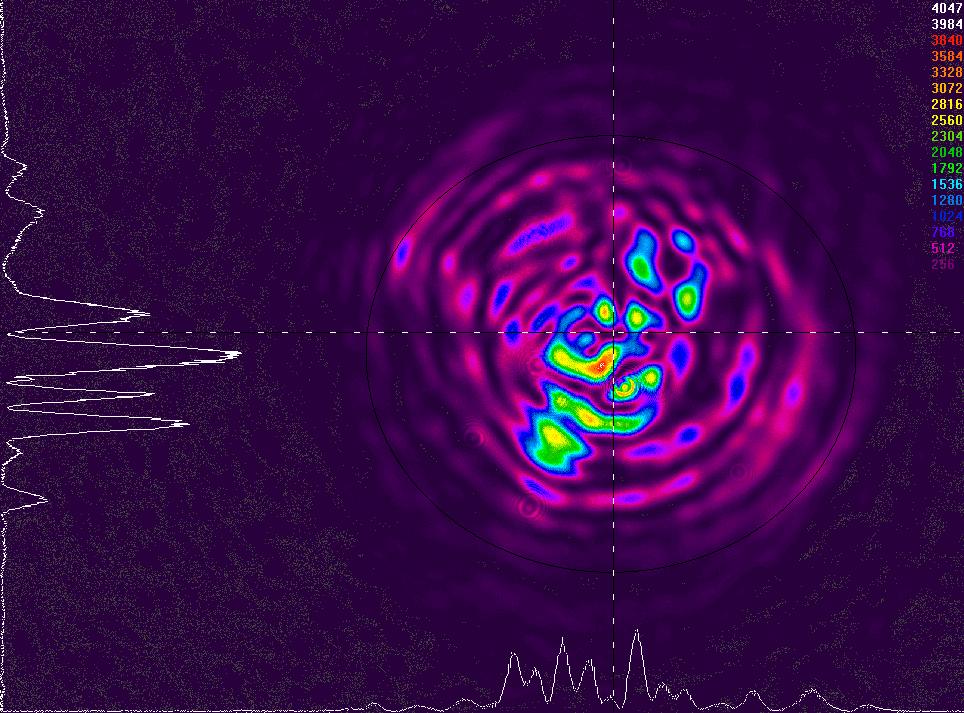
Observation des interférences des modes en champ lointain à z = 103 mm (Après soudure automatique)
Pour conclure, nous avons après plusieurs mesures décidé de prendre pour longueur de référence z= 9 mm, cette longueur, longueur de ré-imagerie du mode excitateur de la fibre multimode, nous permettra, dans une prochaine partie de développer un capteur de courbure.

Expérience 1 Interférences multimodales
Expérience 2 Ré-imagerie
Qu'est-ce que la ré-imagerie ?
Nous allons dans cette partie, après avoir soudé une fibre monomode à une fibre multimode, essayer de déterminer la longueur de la fibre multimode nécessaire pour avoir réimagerie du mode excitateur de la fibre multimode, c'est à dire on cherche la longueur pour laquelle on aura un maximum d'intensité au centre de la figure d'interférence. Nous avons choisit d'étudier seulement les modes LP0m ( Voir partie théorique: ici ), dont la forme représente des anneaux concentriques. D'après la formule (dans le rapport) suivante, on peut calculer facilement la longueur de ré-imagerie:
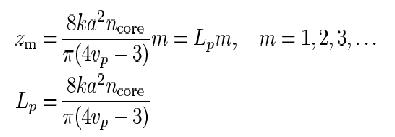
ncore est l’indice du cœur de la fibre ncore = 1.45
a est la taille du rayon du cœur de la fibre : a = 62.5 µm
k = 2π/λ avec λ la longueur d’onde du laser : λ = 632.8 nm
ʋp représente l'ordre du mode LP0ʋ et sa valeur est choisie grâce à la courbe suivante prélevée de l'article[réf1]:

Pour a = 52.5 µm on a V = k.a.ON = 67.7 à 1.55 µm
Pour a = 92.5 µm on a V = 119
Dans l'article, la fibre a une différence d'indice de réfraction: ∆n = 1.479-1.444 = 0.035 (à 1.55 µm) ON = 0.318.
Or dans notre cas, V = 657, mais comme l'article montre que seulement quelques modes LP0m sont excités, on peut dire donc qu'on est dans la même situation et utiliser la courbe ci-dessus.
Le rayon du cœur de notre fibre est de 62.5 μm, la courbe de ƞʋ en fonction de ʋ correspondante est donc comprise entre ces deux courbes (a=52.5 μm et a=92.5 μm). ʋp correspond au maximum de la courbe. Nous choisissons ʋp = 5.
En effectuant le calcul, on trouve donc: Lp = 8.42*10-3m En prenant différentes valeurs de m on trouve bien des multiples de 8.42 :
Pour m = 1, z = 8.42mm
Pour m=2, z = 17 mm
Pour m=3, z = 25.5 mm
pour m=4, z= 33 mm etc.
Nous allons à présent effectuer les observations des interférences des modes sortant d'une fibre monomode soudé à une fibre multimode de différents longueurs de z.
On s'attend donc à avoir la réimagerie du mode fondamental à ces valeur de z (maximum d'intensité au centre de l'image)
Expérience: détermination de la longueure de ré-imagerie
Protocole
On soude maintenant notre fibre monomode initiale à une fibre multimode sans cœur de diamètre=125 μm et d'indice de la gaine n=1 (car c'est l'air) comme sur le schéma qui suit:

On fait varier, ensuite, la longueur z de la fibre multimode afin de pouvoir observer la superposition des modes à la sortie de notre système et de trouver ainsi la longueur de ré- imagerie du mode fondamental (voir la partie théorique).
Pour pouvoir tenir la fibre, lorsqu’on veut la cliver à une distance assez petite, par exemple enlever 1mm, on doit rallonger notre fibre multimode. Pour cela on soude un autre tronçon de fibre quelconque à chaque fois avant le clivage. A la fin on vérifie si le clivage a été bien fait avec la soudeuse.
Résultats
On commence par observer l'interférences des modes à la sortie de notre système (SMF-MMF) en prenant une longueur à peu près z= 9 mm. On obtient donc l'image suivante:


Puis on prend une longueur de la fibre multimode z = 27mm:

Après avoir varié plusieurs fois la longueure de la fibre multimode, on obtient une longueure très interressante à savoir z=33 mm:

Interprétation
On constate qu’il existe plusieurs valeurs de z ou l’intensité est maximale au centre : 9 mm, 18 mm, 27 mm, et 33 mm. Ceci représente la ré-imagerie du mode fondamental.
On constate également que ces longueurs sont pratiquement des multiples de 9, en effet cela correspond aux longueures de ré-imagerie théoriques calculées précedemment.
La meilleur observation que nous avons obtenu est celle de 33mm, en effet c'est celle qui se rapproche le plus de la théorie:
avec m=4 on z= 4*8.42 = 33.68 mm.
Influence du clivage sur les résultats
En faisant nos mesure, nous avons constaté sur quelques images (comme nous le voyons sur l'image qui suit) une forte intensité suivant un axe transverse et une intensité très faible ailleurs, ceci peut être dû à un mauvais clivage.


Influence de la soudure sur les résultats
Durant nos expériences, on a obtenus des images sur lesquelle on a une concentration de l'intensité lumineuse suivant un axe transvers malgrès le bon clivage,on a alors effectué des images des interférences des modes avant et après soudure automatique, on obtient les images suivantes :


Conclusion
Pour conclure, nous avons après plusieurs mesures décidé de prendre pour longueur de référence z= 9 mm, cette longueur, longueur de ré-imagerie du mode excitateur de la fibre multimode, nous permettra, dans une prochaine partie de développer un capteur de courbure.